| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 4 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 8 | Dominater069 | 154 |
| 8 | nor | 154 |
Всем доброго времени суток. Столкнулся с задачами на LCA в которых нужно отвечать на запрос за 1, читал e-maxx столкнулся с множеством алгоритмов которые решают данную проблему хотелось бы узнать что вы чаще всего используете для решение таких задач.
UPD Всем спасибо за помощь, я остановился на двоичном подъёме.
http://e-maxx.ru/algo/lca_linear
Тут описывается, как эту задачу свести к задаче нахождения минимума на отрезке. А эту задачу можно решать(без запросов на модификацию) при помощи sparse table за препроцесс O(NlogN) и запрос за O(1).
Если нужно решить за O(1) в онлайне, то лучше свести к задаче минимум на отрезке и там юзать sparce table (Ибо Фарах-колтон из-за большой константы работает столько же). А если запросы даны в оффлайне использую Тарьяна (считает в сумме за O(N)).
Двоичный подъем. Алгоритм короткий, простой, и хотя асимптотика O(logN) на запрос, константа у алгоритма совсем маленькая.
Вот только памяти столько же жрёт :(
На контестах это редко является проблемой.
Лично у меня ни разу на контестах не было проблем с тем, что двоичный подъем не заходит по памяти. А так — конечно, можно поизвращаться со сведением к RMQ и даже с алгоритмом RMQ за O(log * N) с препроцессингом за
— он еще относительно практичный.
Кстати, алгоритм таков. Разбиваем массив на отрезки длины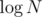
, находим на каждом из них RMQ, получаем массив RMQ размера 
. Строим по полученному массиву Sparse Table (память, очевидно, O(N))). Теперь мы можем находить RMQ за 
— одним запросом к Sparse Table и проходом оставшихся хвостов тупым алгоритмом. Чтобы не проходить хвосты втупую, можно для каждого из блоков размера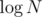 
рекурсивно построить Sparse Table, и так далее для еще меньших блоков, пока блоки в конце концов не станут единичного размера — у нас получится своеобразное дерево глубиной O(log * N).
зачем что-то рекурсивно строить для блоков размера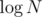
, то есть на практике меньше 20? Заводим 2 массива с минимумами на префиксах и на суффиксах для каждого блока. Тогда тупым алгоритмом придется обрабатывать лишь небольшую (
) часть запросов, у которых обе границы лежат внутри одного блока, а все остальные будут работать за константу.
А почему бы не сделать тесты, в которых все запросы будут именно "плохие"?
тогда будет работать за log с очень небольшой константой. А чтобы получить честный O(1), придется применить трюк четырех русских, вернувшись таким образом к фарах-колтону и бендеру :)
Алгоритм Тарьяна меньше памяти потребляет, чем двоичный подьем? Так как вот это задача не укладывается по памяти с помощью последнего http://informatics.mccme.ru/mod/statements/view3.php?id=1089&chapterid=2787#1
Да. И название задачи какбэ намекает.
Да это я знаю, просто хотелось запихнуть туда двоичный подъем, так как сейчас его реализовывал, спасибо.
Вы построили дерево явно, да еще и на векторах? Разумеется, у Вас ничего не уложится, т.к. у вектора изначальный размер вроде бы 10 (зависит от реализации, но я где-то такую цифру видел).
Задачу можно решить двоичным подъемом немного по-другому, идея была описана в комментариях к моему посту. Если написать все аккуратно, то такое решение просто обязано зайти.
Ну строил я на массивах и явно, просто там ограничения 5 *10^5 вершин. А как я понял памяти съест двоичный подъем n * log (n), еще я писал на Java и наверно не оптимально, то думаю не зайдет. Сейчас попробую Тарьяном. Спасибо.
Я подсчитал расход по памяти при аккуратной реализации, получается 42 МБ. Вам не интересно разобраться, почему Вы все-таки получаете MLE? :)