Всем привет!
Буду краток. Возможно ли искать число K-инверсий быстрее, чем за 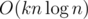 ? Если да, то как? Если нет, то почему?
? Если да, то как? Если нет, то почему?
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Всем привет!
Буду краток. Возможно ли искать число K-инверсий быстрее, чем за 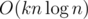 ? Если да, то как? Если нет, то почему?
? Если да, то как? Если нет, то почему?
| Название |
|---|



Для начала не мешало бы пояснить, что такое k-инверсия. Гугл выдает одной из первых ссылок задачу на e-olimp где говорится, что это убывающая подпоследовательность длины k в перестановке.
Если так, то есть подозрение, что нельзя быстрее. Ведь тогда получится искать обычные инверсии быстрее O(n*log n), а вроде быстрее нельзя(я не уверен, но о таком алгоритме никогда не слышал)
Необязательно. Вдруг есть алгоритм за ? Или за какие-нибудь
? Или за какие-нибудь  ...
...
Если кого интересует определение K-инверсий — это, как правильно заметил shef_2318, число убывающих подпоследовательностей длиной K в перестановке длиной N. Задача с тимуса, например: 1523
А почему нельзя искать кол-во обычных, 2-инверсий быстрее ?
?
А нельзя?
А какое-нибудь дерево ван Эмде Боаса умеет находить порядковый номер элемента быстро? Если да, то, похоже, можно за какие-нибудь :)
:)
Дерево ван Эмде Боаса будет работать только с числами, причем сторого говоря за .
.
Инверсии ищутся в перестановках, так что maxNum=n. И, наверное, имелось в виду "с натуральными числами". И да, не знаю структуры этого дерева (всё никак не доберусь), но maxNum подозрительно напоминает использование дерева отрезков. Но в нём его в оценке можно избежать, а тут?
Нет, увы, дерево ван Эмде Боаса жестко завязано на битовых операциях и имеет известные проблемы с памятью из-за этого (если что, первые ссылки в гугле — на хабр и на конспекты ИТМО позволяют бегло посмотреть, что оно умеет, особо не вникая в детали). По смыслу оно не похоже ни на одно из привычных деревьев.
А по поводу задачи — если рассматривать перестановки, то да, можно решать задачу быстрее, однако, если обойтись меньшим и требовать от входных данных только оператора сравнения (что, казалось бы, более логично, чем ограничиваться перестановками), то задача становится слишком похожей на сортировку и интуитивно понятно, что вряд ли получится что-то меньшее, чем , хотя строгих рассуждений привести не могу.
, хотя строгих рассуждений привести не могу.
А его вообще имеет смысл использовать когда-либо? :)
Только как быстрый set<unsigned [long long] int> со здоровым оверхедом по памяти.
Я сравнивал свою не очень оптимизированную реализацию с обычным set — получилось раза в 2.5 быстрее, раза в 3-4 больше памяти (тесты были порядка 10^7 запросов случайные и не очень). Верю, что можно прилизать константу еще немного.
Может, где-то на практике и надо, но что-то сомнительно.
Так ведь для long long int у нас будет 2^32 памяти и более?
Если всю структуру дерева формировать всю и сразу, то да. Однако, если создавать вершины только по необходимости, то выходит (в худшем случае) что-то около созданных вершин на один запрос.
созданных вершин на один запрос.
При случайных запросах даже это не достигалось, эмпирически было похоже на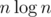 памяти.
памяти.
Не могу сходу оценить — эта последовательность имеет предел?
Она конечна :)
А вообще, я просто неправильно прочитал предыдущий комментарий, действительно, для long long int нужно создать корень, который будет весить 2^32, так что печально все.
Ну, подытоживая, скажу, что можно использовать для чисел бит до 45, наверное, более или менее адекватно.
Не, я имею в виду, можно ли как-то сжато оценить эту последовательность. Типа n/2+n/4+...=O(n). n+n/2+n/3+n/4+...=O(nlogn)
Ну, не более точно, но все же тут главное слагаемое — первое.
точно, но все же тут главное слагаемое — первое.
Выходит, расход памяти и времени порядка ?
?
Обычно оценивают время как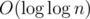 , именно такое время тратится на поиск. С памятью разговор отдельный — при ленивом построении оценивают обычно амортизированно.
, именно такое время тратится на поиск. С памятью разговор отдельный — при ленивом построении оценивают обычно амортизированно.
И какая амортизированная оценка?.. Вообще я слышал, что суммарная оценка времени не может быть ниже суммарной оценки памяти
Это безусловно. Окей, постараюсь внести предельную ясность.
Мы имеем структуру, которая занимает O(n) памяти с операцией за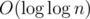 . Это самое обычное дерево.
. Это самое обычное дерево.
Далее, мы пробуем сделать его ленивым. Мы, конечно же, теряем realtime-оценку на операции, потому что выделение массивов не бесплатное. Получаем, строго говоря, оценку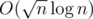 .
.
Однако, в этом подходе разумно все же раздельно оценивать операции поиска и выделения памяти, по двум причинам.
Первая состоит в том, что оценка на количество появившихся вершин сильно завышена. Например, если запросов порядка 107 при n = 232, понятно, что дерево после первой сотни тысяч запросов будет более или менее полным и будет около константы выделений памяти на запрос.
Вторая в том, что аллокация памяти — вещь странная, зависящая от системного хипа, если мы едим память из хипа. Выделение сырого куска памяти может стоит случайно меньше, чем его размер.
Так а какая ассимптотика всё же выйдет в худшем случае? Есть тесты, где при ленивом построении выйдут все ?
?
Во-первых, там будет , а во-вторых, в это не верю, верю, однако, во что-то близкое к
, а во-вторых, в это не верю, верю, однако, во что-то близкое к  , но при достаточно малых q, видимо как раз порядка корня.
, но при достаточно малых q, видимо как раз порядка корня.
Хотя, можно за n / 2k запросов отстроить все дерево, кроме последних k уровней, но что-то я туплю, сколько это добро выжрет памяти, есть подозрение, что около n1 - 2 - k
Да, это вроде верно, но в среднем на запрос тогда получается , что с ростом k вроде как растет и худшее, что получается, это случай единственного запроса, который не очень интересный. Судя по всему, в этом и суть — сначала операции медленные, потом дело идет гораздо веселее.
, что с ростом k вроде как растет и худшее, что получается, это случай единственного запроса, который не очень интересный. Судя по всему, в этом и суть — сначала операции медленные, потом дело идет гораздо веселее.
Однако амортизировать это точнее как-то трудновато, можно поискать статьи на эту тему.
Выше написал что, если пытаться максимизировать память на запрос. С другой стороны видно, что для построения полного дерева нам будут нужны Ω(n) запросов и все они будут обработаны за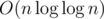 в сумме.
в сумме.
A maxNum?
Во всех моих ответах подразумевалось, что n = maxNum, а где надо использовать количество запросов, оно обозначено за q. Так что я не очень понимаю, что не так с maxNum.
А, понял. Многовато выходит, да. А в сверхбыстром цифровом боре, который, вроде, с такой же ассимптотикой на запрос работает тоже есть такие проблемы с памятью?
Тут можно поглядеть наивную реализацию и чуть-чуть ее сравнить с set'ом. Где-то у меня еще были тесты чуть более сложные (пытался строить макстест, почти получалось), но я пока не могу найти.
One can find the number of inversion in a permutation in time : http://people.csail.mit.edu/mip/papers/invs/paper.pdf . In the same paper there is an algorithm that finds an approximate number of inversions in linear time.
: http://people.csail.mit.edu/mip/papers/invs/paper.pdf . In the same paper there is an algorithm that finds an approximate number of inversions in linear time.
Мм, круто. А такое решение применимо к k-инверсиям? И да, в статье упоминается дерево ван Эмде Боаса, но говорится о другом алгоритме. Разве есть какие-то помехи тому, чтобы использовать это дерево для решения за ?
?
P.S. Зачем писать по-английски в русской ветке? Оо
Чтобы сделать информацию доступной всем.
Так много англоязычных людей зависают на русской версии сайта, ага.
Конкретно мой коммент не нес никакой ценности, а тот, о котором говорим — вполне.
Я о том, что ветка видна только на русской версии сайта. Язык ветки определяется первым комментарием в ней. На самом деле, этот блог даже не появляется в эфире в английской версии сайта, так что...
Некоторые ребята гугл-транслейтят русскую вресию...
Обычно это случается если человек оказался за компом не имеющим русской клавиатуры или раскладки в ОС. Не все транслитом любят пользоваться — а иных он просто бесит... :)
Это уже логичнее... Не подумал сразу :)