Recently I was recommended the problem CERC'10 J — Justice for All. I really liked the solution I came up with and it's different from the editorial, so here's a blogpost talking about it.
Problem
You are given a number $$$n$$$ and you want to create a bipartite graph with $$$n$$$ perfect matchings, $$$1 \leq n \leq 10^6$$$.
The number of nodes in the graph shouldn't exceed $$$400$$$.
Main Idea
We want to build a kind of graph whose number of perfect matchings can be expanded.
If the graph has $$$x$$$ perfect matchings, we want to be able to expand it so that the new graph now has either $$$2x$$$ or $$$2x+1$$$.
If it's possible to do this, then we can use the binary representation of $$$n$$$ to create the graph.
Solution
Locking Mechanism
The idea for doubling is simple, we just need to add a graph with two matchings in such a way that it doesn't disturb the configurations that were previously there. Such graph with two matchings can simply be a square:

Now for doubling and adding one, we can keep the idea of adding a square, but after adding it we need some kind of locking mechanism that either forces a specific configuration of the whole graph or doesn't disturb the configurations that were already there.
We can see the idea of a locking mechanism on a small graph.
Without the locking edge, it has $$$2$$$ perfect matchings.
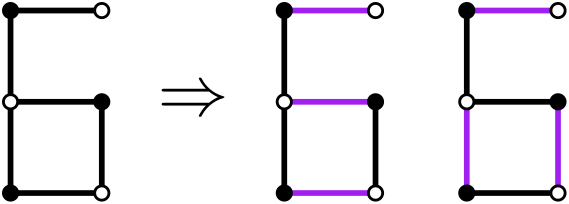
With the locking edge, it has $$$3$$$ perfect matchings. When the locking edge is selected the configuration of the whole graph is forced, otherwise it's the same as if there was no locking edge.
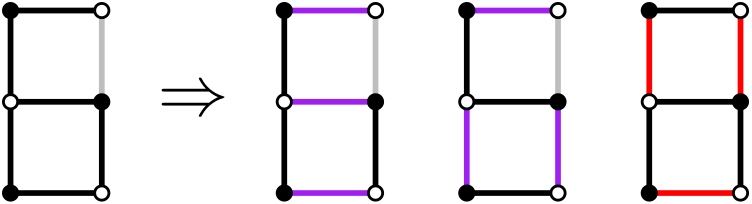
This idea for one square can be extended to lock a chain of squares:
If the locking edge is selected, the configuration of the whole chain is locked. If it's not selected, each square is independent.

Extending $$$x \rightarrow 2x+1$$$
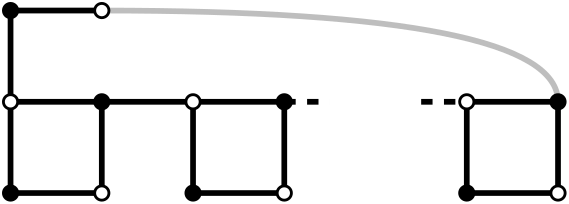
Now we can see that these chains can be extended.

By extending and adding a locking edge, the same previous scenarios can happen:
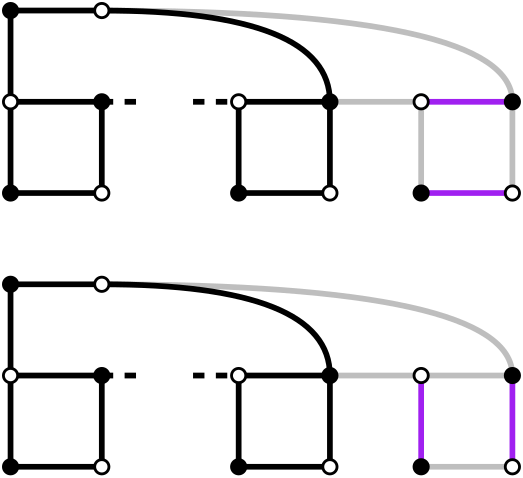
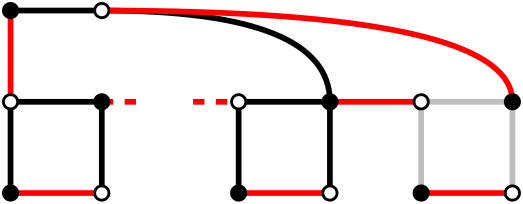
So if the previous chain had $$$x$$$ perfect matchings, this extension now has $$$2x+1$$$.
Extending $$$x \rightarrow 2x$$$
By extending and not adding the locking edge, we just don't have the locked configuration:
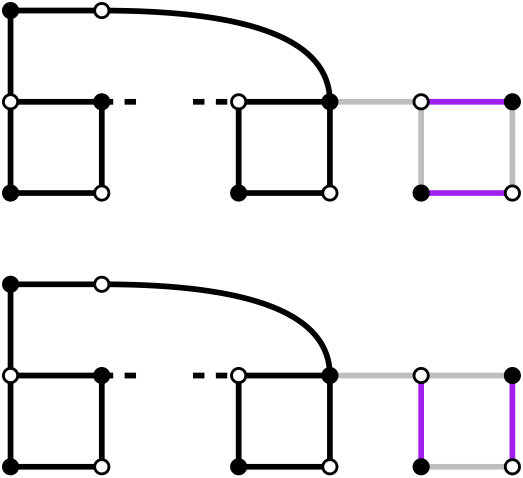
If the chain had $$$x$$$ perfect matchings, this extension now has $$$2x$$$.
So this is it. We found a procedure that lets us extend a chain in the manner we wanted.
Construction
We start with a simple edge with $$$1$$$ perfect matching:

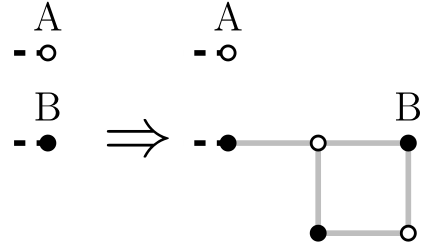
If we have a graph with $$$x$$$ perfect matchings and we want to make it $$$2x$$$, we add a square without a locking edge:
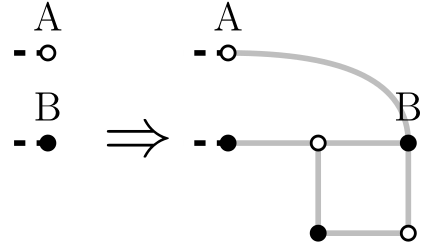
If we have a graph with $$$x$$$ perfect matchings and we want to make it $$$2x+1$$$, we add a square with a locking edge:
Analysis
We want the number of nodes to be less or equal to $$$400$$$.
This construction starts with $$$2$$$ nodes and adds $$$4$$$ for each bit in $$$n$$$ below the most significative.
So this solution has at most $$$4\lfloor \log_2(10^6) \rfloor+2 = 78$$$ nodes, which fits very comfortably below the limit.
Note: the official solution follows a similar idea, but adds 6 nodes for increasing by one and for doubling, resulting in $$$214$$$ nodes in the worst case
Code
The code for this is surprisingly short.
Here is an accepted submission (you may need coach mode to access it).










OTZ