Motivation
I remember struggling to understand the Tarjan algorithm for Strongly Connected Components. The algorithm feels intuitive to me now and I no longer feel this struggle, but what I do still remember is feeling the lack of some good online resource to guide me through it. This is my attempt to write the article I wish I had read.
Directed DFS tree
Before we get to the problem, we have to first understand the most important concept: directed DFS trees. Understanding them will allow for the Tarjan algorithm to feel like a natural extension (and this article is actually about them, not about Tarjan).
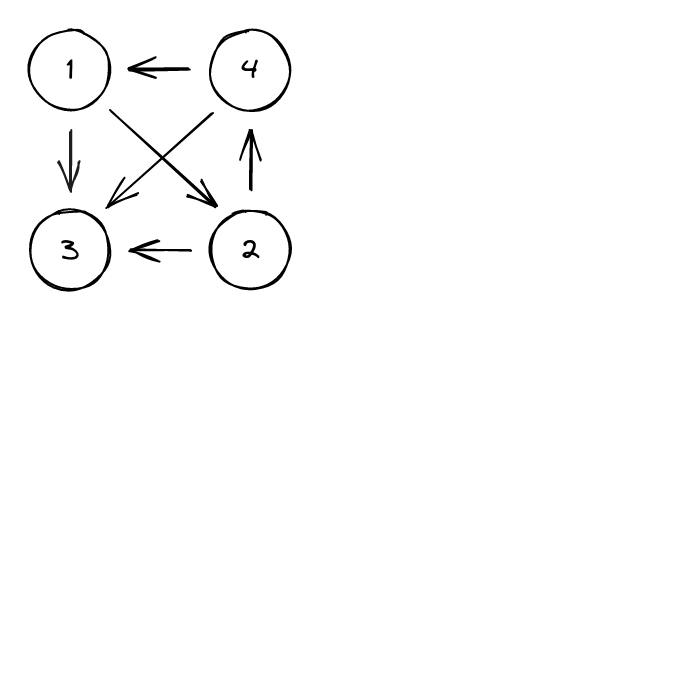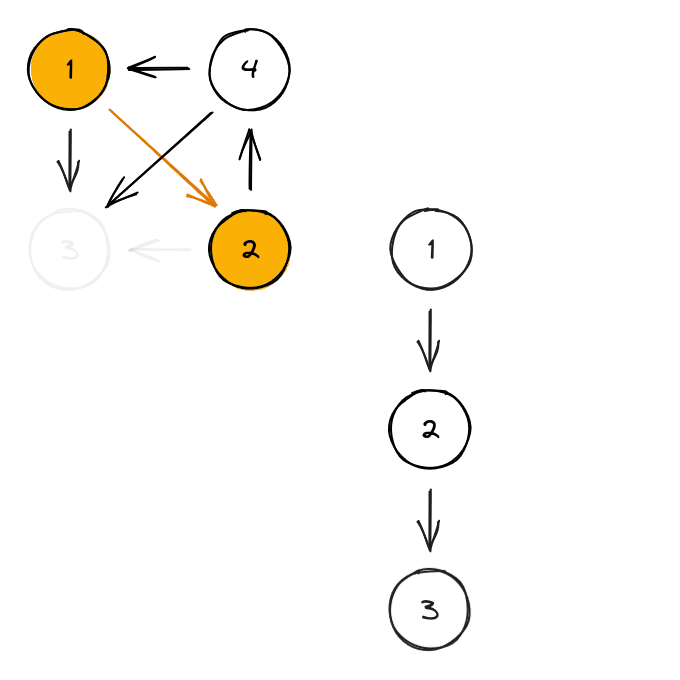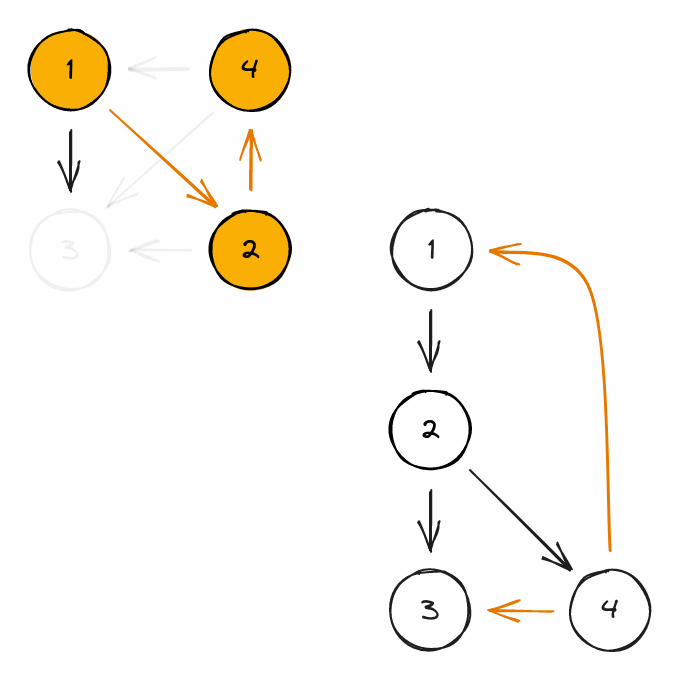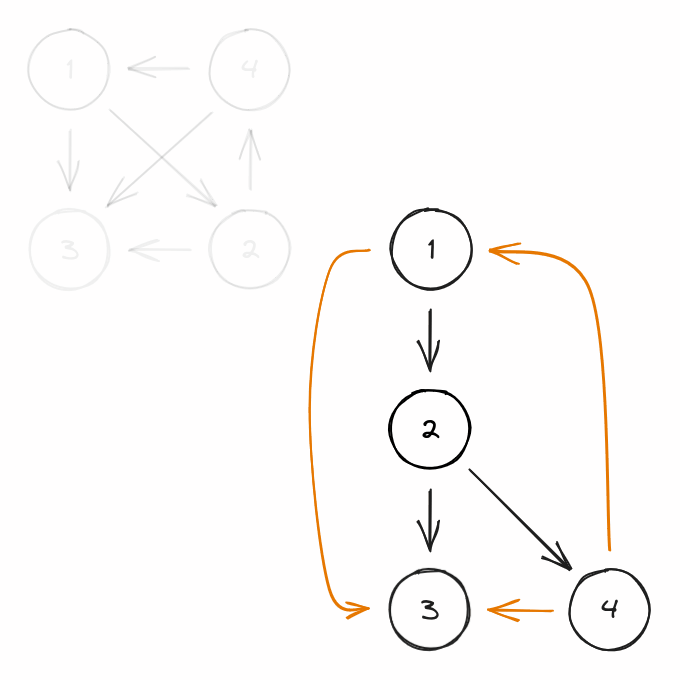
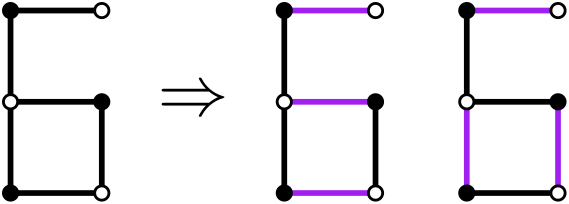
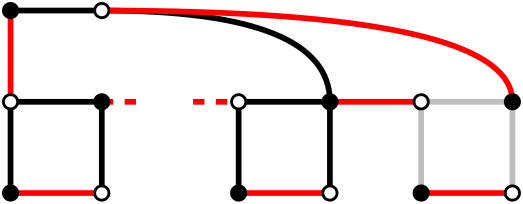
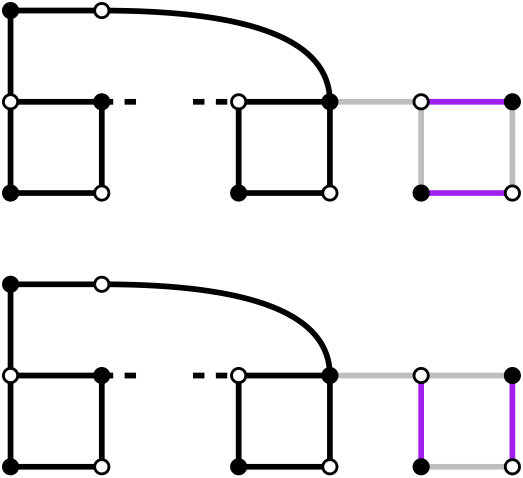
A directed DFS tree is an explicit representation of a DFS traversal of a directed graph.
When a node is visited for the first time, it is added to the tree, either as a root if it was visited in the beginning of a DFS call, or as the child of the node it got visited from.
The edges that were used to visit a node for the first time will be considered as part of the tree and be called tree-edges.
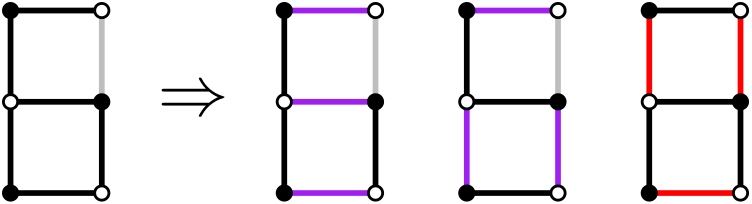
Every other edge of the graph will be described in relation to this tree:
- a forward-edge is an edge that connects a node to a descendant.
- a back-edge is an edge that connects a node to an ancestor.
- a cross-edge is any other edge.
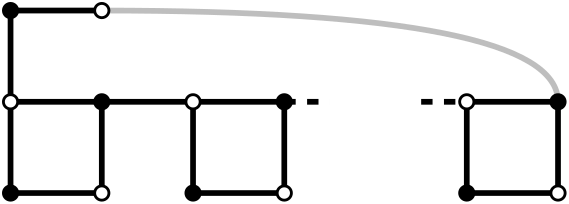
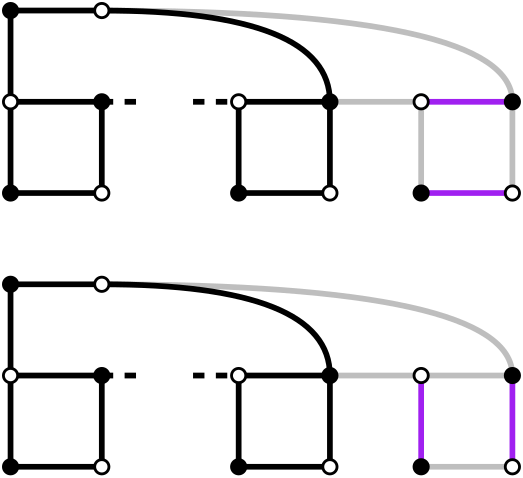
Here is an example of the construction of a tree, with every kind of edge: