Thank you for participation and we hope you enjoy this round :)
D2A — Shuffle Party
Idea : chromate00
If you think in terms of $$$k$$$, it might be hard to find the solution. Maybe it will be helpful if you fix $$$d$$$ and find the $$$k$$$ which will be swapped with $$$d$$$.
Try bruteforcing for, say, $$$n \le 20$$$. Do you see a pattern?
On $$$n=1$$$, the answer is trivially $$$1$$$.
On $$$n=2$$$, index $$$1$$$ and $$$2$$$ are swapped. The answer is therefore $$$2$$$.
For $$$n>2$$$, let us assume the element $$$1$$$ is on index $$$a$$$ and it will be swapped with index $$$k$$$. Then, $$$a$$$ must be $$$k/2$$$. We will prove this by contradiction. Let us assume that there is no divisor greater than $$$a$$$, and $$$a$$$ is lesser than $$$k/2$$$. But then, as $$$a$$$ is a multiple of $$$2$$$ in the base condition, $$$k$$$ must be a multiple of $$$2$$$, and $$$k/2$$$ is a divisor of $$$k$$$. This contradicts the assumption. By induction we can see that $$$a$$$ is always a multiple of $$$2$$$, and this proof will always hold. The element $$$1$$$ will move only when $$$k/2=a$$$.
Therefore, we can find the largest value of $$$v$$$ such that $$$2^v \le n$$$. The answer turns out to be $$$2^v$$$.
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
int main()
{
cin.tie(0)->sync_with_stdio(0);
ll q;cin>>q;
while(q--)
{
ll n,p=1;cin>>n;
while(p*2<=n)p<<=1;
cout<<p<<"\n";
}
}
Video editorial by aryanc403 https://www.youtube.com/watch?v=lLmVzA49BRM
D2B — Binary Path
Idea : wuhudsm
Let’s call path $$$(1,1) \rightarrow \ldots \rightarrow (1,i)\rightarrow(2,i) \rightarrow \ldots \rightarrow (2,n)$$$ the $$$i$$$-th path. What's the difference between the $$$i$$$-th path and the $$$(i+1)$$$-th path?
What if $$$a_{2i}=1$$$ and $$$a_{1(i+1)}=0$$$ ?
What if $$$a_{2i}=0$$$ and $$$a_{1(i+1)}=1$$$ ?
Let the string achieved by moving down on the $$$i$$$-th column be $$$S_i$$$. Then, for any $$$1 \le k < n$$$, one can observe that $$$S_k$$$ and $$$S_{k+1}$$$ can only differ by at most one index, which is index $$$k+1$$$. Thus, comparing $$$S_k$$$ and $$$S_{k+1}$$$ lexicographically can be done in $$$O(1)$$$, by comparing this one index.
After finding the lexicographically smallest string, counting the occurrence of this string can be done straightforwardly in $$$O(n)$$$.
The implementation can differ for each participant, but the following method provides a clean implementation. Let the initial coordinate be $$$(1,1)$$$, and maintain a counter which is initially reset to $$$1$$$. Then repeat the following until we reach $$$(2,n)$$$:
- If we are on row $$$2$$$, move to the right.
- If we are on column $$$n$$$, move downwards.
- From here, let the character on the right be $$$a$$$, and one below be $$$b$$$.
- If $$$a>b$$$, move downwards.
- If $$$a<b$$$, move to the right and reset the counter to $$$1$$$.
- If $$$a=b$$$, move to the right and increment the counter.
- In the end, the string on the path we passed through will be lexicographically smallest, and the integer on the counter will be the number of occurrences.
#include <map>
#include <set>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <cstdio>
#include <cstdlib>
#include <vector>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef double db;
typedef long long ll;
typedef unsigned long long ull;
const int N=1000010;
const int LOGN=28;
const ll TMD=0;
const ll INF=2147483647;
int T,n;
char a[3][N];
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=2;i++)
{
scanf("\n");
for(int j=1;j<=n;j++)
scanf("%c",&a[i][j]);
}
int max_down=n,min_down=1;
for(int i=n;i>=2;i--)
if(a[1][i]=='1'&&a[2][i-1]=='0') max_down=i-1;
for(int i=1;i<max_down;i++)
if(a[2][i]=='1'&&a[1][i+1]=='0') min_down=i+1;
for(int i=1;i<=max_down;i++) printf("%c",a[1][i]);
for(int i=max_down;i<=n;i++) printf("%c",a[2][i]);
printf("\n");
printf("%d\n",max_down-min_down+1);
}
return 0;
}
D1A — Bitwise Operation Wizard
Idea : wuhudsm
What's the maximum value of $$$p_i \oplus p_j$$$?
How to get $$$i$$$, such that $$$p_i = n-1$$$?
How to get $$$j$$$, such that $$$p_i \oplus p_j$$$ reaches the maximum value?
Step1:do queries $$$? \ x \ x \ y \ y$$$ like classic searching for the maximum value among $$$n$$$ numbers to get $$$p_i= n-1$$$;
Step2:do queries $$$? \ x \ i \ y \ i$$$ to find all index $$$k$$$ such that $$$p_i | p_{k}$$$ reaches the maximum value. We store all such indexes in a vector $$$id$$$ .
Step3:do queries $$$? \ id[x] \ id[x] \ id[y] \ id[y]$$$ to find $$$j$$$ in $$$id$$$ such that $$$p_j$$$ reaches the minimum value.
#include <map>
#include <set>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <cstdio>
#include <cstdlib>
#include <vector>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef double db;
typedef long long ll;
typedef unsigned long long ull;
const int N=1000010;
const int LOGN=28;
const ll TMD=0;
const ll INF=2147483647;
int T,n;
char query(int a,int b,int c,int d)
{
char x;
printf("? %d %d %d %d\n",a,b,c,d);
fflush(stdout);
cin>>x;
fflush(stdout);
return x;
}
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
int mx=0,ans1=0,ans2;
vector<int> v;
for(int i=1;i<n;i++)
{
int c=query(ans1,ans1,i,i);
if(c=='<') ans1=i;
}
v.push_back(0);
for(int i=1;i<n;i++)
{
int c=query(mx,ans1,i,ans1);
if(c=='<')
{
mx=i;
v.clear();
v.push_back(i);
}
else if(c=='=') v.push_back(i);
}
ans2=v[0];
for(int i=1;i<v.size();i++)
{
int c=query(ans2,ans2,v[i],v[i]);
if(c=='>') ans2=v[i];
}
printf("! %d %d\n",ans1,ans2);
fflush(stdout);
}
return 0;
}
Video editorial by aryanc403 https://www.youtube.com/watch?v=jfcx1Rs8I28
D1B — Pinball
Idea : wuhudsm
UPD: It conflicts with https://mirror.codeforces.com/contest/733/problem/E. This is a coincidence. There are no excuses. Very sorry for any inconvenience caused to everyone.
Observe: which cells actually change the direction of the pinball placed at position $$$p$$$ initially?
These cells are the $$$>$$$ to the left of $$$p$$$ and the $$$<$$$ to the right of $$$p$$$. Can you see the trace of the pinball?
How to quickly calculate the time when a pinball leaves the grid?
We observe that, in fact, only the $$$>$$$ to the left of $$$p$$$ and the $$$<$$$ to the right of $$$p$$$ change the direction of the pinball placed at position $$$p$$$ initially.
For convenience, let's assume $$$s_p$$$ is $$$>$$$, $$$k=min(countright(1,p),countleft(p+1,n))$$$, and the pinball leaves from the left boundary(for other situations, we can handle them in a similar way).
We can obtain $$$right[1,\ldots,k]$$$ and $$$left[1,\ldots,k]$$$ through prefix sum + binary search, where $$$right$$$ represents the indices of $$$>$$$ to the left of $$$p$$$ (in decreasing order), and $$$left$$$ represents the indices of $$$<$$$ to the right of $$$p$$$ (in increasing order).
We use $$$right$$$ and $$$left$$$ to describe the trace of the pinball:
The first segment: the pinball moves from $$$right_1$$$ to $$$left_1$$$;
The second segment: the pinball moves from $$$left_1$$$ to $$$right_2$$$;
The third segment: the pinball moves from $$$right_2$$$ to $$$left_3$$$;
$$$\ldots$$$
The $$$2k$$$-th segment: the pinball moves from $$$left_k$$$ to the left boundary.
It is not difficult to observe that we can use prefix sum to store the sum of indices, and then quickly calculate the time when the pinball moves.
#include <map>
#include <set>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <cstdio>
#include <cstdlib>
#include <vector>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef double db;
typedef long long ll;
typedef unsigned long long ull;
const int N=1000010;
const int LOGN=28;
const ll TMD=0;
const ll INF=2147483647;
int T,n;
ll Sl[N],Sr[N],IDl[N],IDr[N];
char s[N];
int findpre(int x)
{
int L=0,R=n+1,M;
while(L+1!=R)
{
M=(L+R)>>1;
if(Sr[M]<x) L=M;
else R=M;
}
return R;
}
int findsuf(int x)
{
int L=0,R=n+1,M;
while(L+1!=R)
{
M=(L+R)>>1;
if(Sl[n]-Sl[M-1]<x) R=M;
else L=M;
}
return L;
}
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d%s",&n,s);
for(int i=1;i<=n;i++)
{
Sr[i]=Sr[i-1]+(s[i-1]=='>');
Sl[i]=Sl[i-1]+(s[i-1]=='<');
IDr[i]=IDr[i-1]+i*(s[i-1]=='>');
IDl[i]=IDl[i-1]+i*(s[i-1]=='<');
}
for(int i=1;i<=n;i++)
{
if(s[i-1]=='>')
{
if(Sr[i]>Sl[n]-Sl[i])
{
int p=findpre(Sr[i]-(Sl[n]-Sl[i]));
printf("%I64d ",2*((IDl[n]-IDl[i])-(IDr[i]-IDr[p-1]))+i+(n+1));
}
else
{
int p=findsuf((Sl[n]-Sl[i])-Sr[i]+1);
printf("%I64d ",2*((IDl[p]-IDl[i])-(IDr[i]-IDr[0]))+i);
}
}
else
{
if(Sr[i]>=Sl[n]-Sl[i-1])
{
int p=findpre(Sr[i]-(Sl[n]-Sl[i-1])+1);
printf("%I64d ",2*((IDl[n]-IDl[i-1])-(IDr[i]-IDr[p-1]))-i+(n+1));
}
else
{
int p=findsuf((Sl[n]-Sl[i-1])-Sr[i]);
printf("%I64d ",2*((IDl[p]-IDl[i-1])-(IDr[i]-IDr[0]))-i);
}
}
}
printf("\n");
}
return 0;
}
D1C — Pokémon Arena
Idea : wuhudsm
In fact, you don't need to hire the same Pokemon more than once.
Consider graph building.
How to reduce the number of edges in the graph?
Let's consider $$$n$$$ Pokémon as nodes, and defeating Pokémon $$$u$$$ by Pokémon $$$v$$$ as the edge $$$u \rightarrow v$$$. Then the problem is essentially finding the shortest path from $$$n$$$ to $$$1$$$.
If we brute force to construct the graph, the time complexity will be $$$O(n^2m)$$$, which is unacceptable. How can we find a better way to build the graph?
Recalling, we need to represent all processes like "Pokémon $$$u$$$ increased attribute $$$x$$$ by some value and defeated Pokémon $$$v$$$" using paths in the graph.
We will use the following graph building to achieve this. Overall, we consider each attribute separately. For the $$$x$$$-th attribute, we construct $$$2n$$$ virtual nodes $$$X_1,...,X_n$$$ and $$$Y_1,...,Y_n$$$, and connect each Pokémon based on the $$$x$$$-th attribute.
For example, $$$n=3$$$ and $$$a_{1,1}=9, a_{2,1}=6, a_{3,1}=1$$$, we have the following graph building for attribute $$$1$$$:
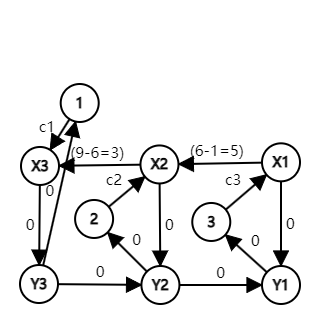
In this graph,for example,"Pokémon $$$3$$$ increased attribute $$$1$$$ by $$$8$$$ and defeated Pokémon $$$1$$$" can be represented as path $$$3 \rightarrow X1 \rightarrow X2 \rightarrow X3 \rightarrow Y3 \rightarrow 1$$$.
More generally, our graph building method is :
Consider each attribute separately. Assuming we are processing the $$$i$$$-th attribute, insert all $$$a_{1,i} , \ldots ,a_{n,i}$$$ into $$$val$$$ and sort it (for convenience, we assume that they are pairwise different).
Construct $$$2n$$$ virtual nodes $$$X_1,...,X_n$$$ and $$$Y_1,...,Y_n$$$;
Add edge $$$X_i \rightarrow X_{i+1}$$$ with a value of $$$(val_{i+1}-val_i)$$$ for $$$1 \le i < n$$$;
Add edge $$$Y_{i+1} \rightarrow Y_{i}$$$ with a value of $$$0$$$ for $$$1 \le i < n$$$;
Add edge $$$X_i \rightarrow Y_{i}$$$ with a value of $$$0$$$ for $$$1 \le i \le n$$$;
Add edge $$$i \rightarrow X_{rank_i}$$$ with a value of $$$c_i$$$ for $$$1 \le i \le n$$$;
Add edge $$$Y_{rank_i} \rightarrow i$$$ with a value of $$$0$$$ for $$$1 \le i \le n$$$.
Then we just run Dijkstra algorithm in this graph. The time complexity is $$$O(nmlog(nm))$$$.
#include <bits/stdc++.h>
#define int long long
#define fi first
#define se second
using namespace std;
const int INFF = 1e18;
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while (t --> 0) {
int n, m;
cin >> n >> m;
vector<int> c(n + 1);
for (int i = 1; i <= n; i++) cin >> c[i];
vector<vector<int>> a(n + 1, vector<int>(m + 1));
vector<vector<pair<int, int>>> b(m + 1);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
b[j].push_back({a[i][j], i});
}
}
vector<vector<int>> rank(n + 1, vector<int>(m + 1));
vector<vector<int>> dec(n + 1, vector<int>(m + 1));
for (int j = 1; j <= m; j++) {
sort(b[j].begin(), b[j].end());
for (int i = 0; i < n; i++) {
auto [x, id] = b[j][i];
rank[id][j] = i + 1;
dec[i + 1][j] = id;
}
}
int ans = INFF;
vector<int> vis(n + 1, 0);
vector<vector<int>> dist(n + 1, vector<int>(m + 1, INFF));
priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> pq;
vis[1] = 1;
for (int j = 1; j <= m; j++) dist[1][j] = 0, pq.push({dist[1][j], 1, j});
while (!pq.empty()) {
auto [w, x, t] = pq.top();
pq.pop();
if (dist[x][t] < w) continue;
if (x == n) ans = min(ans, w + c[n]);
if (rank[x][t] < n) {
int z = dec[rank[x][t] + 1][t];
if (w < dist[z][t]) {
dist[z][t] = w;
pq.push({dist[z][t], z, t});
}
}
if (rank[x][t] > 1) {
int z = dec[rank[x][t] - 1][t];
if (w + a[x][t] - a[z][t] < dist[z][t]) {
dist[z][t] = w + a[x][t] - a[z][t];
pq.push({dist[z][t], z, t});
}
}
if (!vis[x]) {
vis[x] = 1;
for (int j = 1; j <= m; j++) {
if (w + c[x] < dist[x][j]) {
dist[x][j] = w + c[x];
pq.push({dist[x][j], x, j});
}
}
}
}
cout << ans << '\n';
}
return 0;
}
Video editorial by aryanc403 https://www.youtube.com/watch?v=ysdozposXkQ
D1D — Bitwise Paradox
Idea : Psychotic_D, MagicalFlower
First we use the line segment tree to maintain sequence $$$b$$$. For the nodes $$$[l,r]$$$ on each line segment tree, we maintain the first and last occurrence positions of each binary bit in the interval.
We need to merge the two intervals, whether it is modification or query. Suppose you want to use the information of $$$[l, mid], [mid +1, r]$$$ to merge the information of $$$[l, r]$$$. Consider the answer that spans two intervals. If we want to make the $$$i$$$-th position of the interval OR $$$1$$$, then there are two possibilities
Select the last occurrence position $$$P$$$ of the $$$i$$$-th bit in $$$[l,mid].$$$
Select the first occurrence position $$$Q$$$ of the $$$i$$$-th bit in $$$[mid+1,r].$$$
Let $$$x = max(a[P], a[P+1],\ldots, a[mid]), y = max(a[mid + 1], a[mid + 2], \ldots, a[Q]).$$$
If $$$x<=y,$$$ we can choose the position $$$P$$$ greedily, because his price is smaller. If you choose $$$Q,$$$ then you must also choose $$$P,$$$ because choosing $$$P$$$ does not increase max $$$a.$$$ Otherwise, select $$$Q$$$ on the contrary.
With the above greedy, then you can enumerate the first binary bit $$$i$$$ that is larger than $$$v$$$. The $$$i$$$-th bit of the interval OR must be $$$1$$$, and the $$$i$$$-th bit of $$$v$$$ is $$$0$$$. For the $$$j$$$-th $$$(j >i)$$$ bit, if the $$$j$$$-th bit of $$$v$$$ is $$$1$$$, then the $$$j$$$-th bit must also be $$$1$$$. The rest of the bits can be regarded as $$$0$$$ or $$$1$$$, you only need to deal with these bits that must be selected $$$1$$$ greedily, and expand the interval.
You can use the st table $$$O(1)$$$ to find the interval max of $$$a$$$, so you can merge the information of the two intervals in the time of $$$O(log V)$$$. With the line segment tree, $$$O(q log n log V + n log V)$$$ can be done.
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 5e5 + 10, V = 30, inf = INT_MAX, L = 18;
int n, q, S, a[N], b[N];
struct Rmq
{
int st[L][N];
void init()
{
for (int i = 1; i <= n; i++)
st[0][i] = a[i];
for (int i = 1; i < L; i++)
{
for (int j = 1; j <= n - (1 << i) + 1; j++)
{
st[i][j] = max(st[i - 1][j], st[i - 1][j + (1 << i - 1)]);
}
}
}
int qry(int l, int r)
{
int k = __lg(r - l + 1);
return max(st[k][l], st[k][r - (1 << k) + 1]);
}
} ds;
struct Info
{
int pre[V], suf[V];
int ans, l, r;
Info()
{
memset(pre, 0, sizeof(pre));
memset(suf, 0, sizeof(suf));
ans = inf, l = r = 0;
}
Info(const Info &x, const Info &y)
{
for (int i = 0; i < V; i++)
{
pre[i] = x.pre[i] ? x.pre[i] : y.pre[i];
suf[i] = y.suf[i] ? y.suf[i] : x.suf[i];
}
ans = inf, l = r = 0;
}
friend Info operator+(const Info &x, const Info &y)
{
Info z(x, y);
z.ans = min(x.ans, y.ans), z.l = x.l, z.r = y.r;
int pl = x.r, pr = y.l;
if (!pl)
return z;
for (int i = V - 1; i >= 0; i--)
{
int u = x.suf[i], v = y.pre[i];
if (u)
u = min(u, pl);
if (v)
v = max(v, pr);
int lans = u ? ds.qry(u, pr) : inf;
int rans = v ? ds.qry(pl, v) : inf;
if (lans < rans)
{
if (S >> i & 1)
{
if (lans < z.ans)
pl = u;
else
break;
}
else
z.ans = min(z.ans, lans);
}
else
{
if (S >> i & 1)
{
if (rans < z.ans)
pr = v;
else
break;
}
else
z.ans = min(z.ans, rans);
}
}
return z;
}
void clear()
{
*this = Info();
}
void upd(int p)
{
l = r = p, ans = b[p] > S ? a[p] : inf;
memset(pre, 0, sizeof(pre));
memset(suf, 0, sizeof(suf));
for (int j = 0; j < V; j++)
{
if (b[p] >> j & 1)
{
suf[j] = p;
pre[j] = p;
}
}
}
} ans;
void reply(const Info &cur)
{
ans = ans + cur;
}
struct Node
{
Node *ls, *rs;
int l, r, mid;
Info info;
void up()
{
info = ls->info + rs->info;
}
void update(int p)
{
if (l == r)
return info.upd(l);
p <= mid ? ls->update(p) : rs->update(p);
up();
}
void query(int ql, int qr)
{
if (l >= ql && r <= qr)
return reply(info);
if (ql <= mid)
ls->query(ql, qr);
if (qr > mid)
rs->query(ql, qr);
}
} mempool[N + 5 << 1], *cnt = mempool, *rt;
Node *build(int l, int r)
{
Node *u = cnt++;
int mid = l + r >> 1;
u->l = l, u->r = r, u->mid = mid;
if (l == r)
{
u->info.upd(l);
return u;
}
u->ls = build(l, mid);
u->rs = build(mid + 1, r);
u->up();
return u;
}
void solve()
{
cin >> n >> S;
S--;
for (int i = 1; i <= n; i++)
cin >> a[i];
ds.init();
for (int i = 1; i <= n; i++)
cin >> b[i];
rt = build(1, n);
cin >> q;
for (int i = 0; i < q; i++)
{
int opt;
cin >> opt;
if (opt == 1)
{
int p, x;
cin >> p >> x;
b[p] = x;
rt->update(p);
}
else
{
int l, r;
cin >> l >> r;
ans.clear();
rt->query(l, r);
cout << (ans.ans == inf ? -1 : ans.ans) << ' ';
}
}
cout << "\n";
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false), cin.tie(0);
int t = 0;
cin >> t;
while (t--)
{
solve();
}
// cerr << 1.0 * clock() / CLOCKS_PER_SEC << '\n';
return 0;
}
D1E — Yet Yet Another Permutation Problem
Idea : wuhudsm
We found it difficult to directly calculate all valid permutations. How about calculating all invalid permutations?
Can you come up with an $$$O(n^2)$$$ DP solution?
How to optimize the $$$O(n^2)$$$ DP solution?
We found it difficult to directly calculate all valid permutations. Consider calculating all invalid permutations and subtract it from $$$n!$$$.
Let's first make some notes. We note $$$P_i=max(p_1,...,p_i),Q_i=max(q_1,...,q_i)$$$,and $$$last_i=max(j)(P_j \neq P_i)$$$.And note the values of all extreme points is $$$val[1,...,m]$$$ and positions is $$$pos[1,...,m]$$$.
For example,$$$p=[3,1,4,2,6,5]$$$,we get $$$m=3$$$, $$$val=[3,4,6]$$$ and $$$pos=[1,3,5]$$$.
Let’s call a permutation $$$q$$$ “i-invalid” if there’s an index $$$j$$$ satisfying $$$Q_j=P_j=val_i$$$.
Note $$$S_i$$$ as the set of all “i-invalid” permutations.According to the Inclusion-Exclusion Principle,the answer is $$$n!-(|S_1|+|S_2|+...)+(|S_1∩S_2|+|S_1∩S_3|+...)-...$$$
Consider put $$$val_i$$$ in $$$q$$$ to make $$$q$$$ “i-invalid”.There’re $$$2$$$ kinds of ways:
$$$q_j=val_i(1 \le j < pos_i)$$$ and $$$Q_{pos_i}=val_i$$$;
$$$q_j=val_i(pos_i \le j< pos_{i+1})$$$ and $$$Q_{pos_i}=val_i$$$.
In both cases,we call the first $$$max(j,pos_i)$$$ numbers are “determined”. In other words,they’re some numbers in $$$[1,val_i]$$$.
Then we can find an $$$O(n^2)$$$ DP. Note $$$dp_{i,j}$$$ — $$$i$$$ stands for the first $$$i$$$ numbers is “determined”,and $$$j$$$ stands for $$$j$$$ extreme values are “invalid”. In fact we only care about the parity of $$$j$$$,so $$$j=0,1$$$. Note for the first $$$i$$$ numbers are “determined” automatically means $$$Q_i=P_i$$$. In addition,$$$q_i=P_i(P_i=P_{i-1})$$$ or $$$q_i<P_i(P_i \neq P_{i-1})$$$.
We get a DP formula $$$dp_{i,j}= \Sigma_{k=0}^{last_i} dp_{k,j \oplus 1} \cdot A^{P_i-k-1}_{i-k-1} \cdot (P_i==P_{i+1}?1:i-k)$$$
Here is a small trick to reduce the constant. If we note $$$f_i=dp_{i,0}-dp_{i,1}$$$, we get a more concise formula $$$f_{i}= -\Sigma_{j=0}^{last_i} f_{j} \cdot A^{P_i-j-1}_{i-j-1} \cdot (P_i==P_{i+1}?1:i-j)$$$
We perform the following transformation on the formula.
① For $$$i$$$ satisfying $$$P_i=P_{i-1}$$$, we get
$$$f_{i}= -\Sigma_{j=0}^{last_i} f_{j} \cdot A^{P_i-j-1}_{i-j-1} = -[(P_i-i)!]^{-1} \Sigma_{j=0}^{last_i} f_{j} \cdot (P_i-j-1)!$$$
② For $$$i$$$ satisfying $$$P_i \neq P_{i-1}$$$, we get
$$$f_{i}= -\Sigma_{j=0}^{last_i} f_{j} \cdot A^{P_i-j-1}_{i-j-1} \cdot (i-j) = -i[(P_i-i)!]^{-1} \Sigma_{j=0}^{last_i} f_{j} \cdot (P_i-j-1)! + [(P_i-i)!]^{-1} \Sigma_{j=0}^{last_i} jf_{j} \cdot (P_i-j-1)!$$$
After that, we have transformed the formula into a classical form $$$f(i)= h(i) \Sigma_{j=0}^{i-1} f(j) \cdot g(i-j)$$$, which can be calculate in $$$O(n log^2 n)$$$ by D&C+FFT.
#include<bits/stdc++.h>
using namespace std;
#define all(a) a.begin(),a.end()
#define pb push_back
#define sz(a) ((int)a.size())
using ll=long long;
using u32=unsigned int;
using u64=unsigned long long;
using i128=__int128;
using u128=unsigned __int128;
using f128=__float128;
using pii=pair<int,int>;
using pll=pair<ll,ll>;
template<typename T> using vc=vector<T>;
template<typename T> using vvc=vc<vc<T>>;
template<typename T> using vvvc=vc<vvc<T>>;
using vi=vc<int>;
using vll=vc<ll>;
using vvi=vc<vi>;
using vvll=vc<vll>;
#define vv(type,name,n,...) \
vector<vector<type>> name(n,vector<type>(__VA_ARGS__))
#define vvv(type,name,n,m,...) \
vector<vector<vector<type>>> name(n,vector<vector<type>>(m,vector<type>(__VA_ARGS__)))
template<typename T> using min_heap=priority_queue<T,vector<T>,greater<T>>;
template<typename T> using max_heap=priority_queue<T>;
// https://trap.jp/post/1224/
#define rep1(n) for(ll i=0; i<(ll)(n); ++i)
#define rep2(i,n) for(ll i=0; i<(ll)(n); ++i)
#define rep3(i,a,b) for(ll i=(ll)(a); i<(ll)(b); ++i)
#define rep4(i,a,b,c) for(ll i=(ll)(a); i<(ll)(b); i+=(c))
#define cut4(a,b,c,d,e,...) e
#define rep(...) cut4(__VA_ARGS__,rep4,rep3,rep2,rep1)(__VA_ARGS__)
#define per1(n) for(ll i=((ll)n)-1; i>=0; --i)
#define per2(i,n) for(ll i=((ll)n)-1; i>=0; --i)
#define per3(i,a,b) for(ll i=((ll)a)-1; i>=(ll)(b); --i)
#define per4(i,a,b,c) for(ll i=((ll)a)-1; i>=(ll)(b); i-=(c))
#define per(...) cut4(__VA_ARGS__,per4,per3,per2,per1)(__VA_ARGS__)
#define rep_subset(i,s) for(ll i=(s); i>=0; i=(i==0?-1:(i-1)&(s)))
template<typename T, typename S> constexpr T ifloor(const T a, const S b){return a/b-(a%b&&(a^b)<0);}
template<typename T, typename S> constexpr T iceil(const T a, const S b){return ifloor(a+b-1,b);}
template<typename T>
void sort_unique(vector<T> &vec){
sort(vec.begin(),vec.end());
vec.resize(unique(vec.begin(),vec.end())-vec.begin());
}
template<typename T, typename S> constexpr bool chmin(T &a, const S b){if(a>b) return a=b,true; return false;}
template<typename T, typename S> constexpr bool chmax(T &a, const S b){if(a<b) return a=b,true; return false;}
template<typename T, typename S> istream& operator >> (istream& i, pair<T,S> &p){return i >> p.first >> p.second;}
template<typename T, typename S> ostream& operator << (ostream& o, const pair<T,S> &p){return o << p.first << ' ' << p.second;}
#ifdef i_am_noob
#define bug(...) cerr << "#" << __LINE__ << ' ' << #__VA_ARGS__ << "- ", _do(__VA_ARGS__)
template<typename T> void _do(vector<T> x){for(auto i: x) cerr << i << ' ';cerr << "\n";}
template<typename T> void _do(set<T> x){for(auto i: x) cerr << i << ' ';cerr << "\n";}
template<typename T> void _do(unordered_set<T> x){for(auto i: x) cerr << i << ' ';cerr << "\n";}
template<typename T> void _do(T && x) {cerr << x << endl;}
template<typename T, typename ...S> void _do(T && x, S&&...y) {cerr << x << ", "; _do(y...);}
#else
#define bug(...) 777771449
#endif
template<typename T> void print(vector<T> x){for(auto i: x) cout << i << ' ';cout << "\n";}
template<typename T> void print(set<T> x){for(auto i: x) cout << i << ' ';cout << "\n";}
template<typename T> void print(unordered_set<T> x){for(auto i: x) cout << i << ' ';cout << "\n";}
template<typename T> void print(T && x) {cout << x << "\n";}
template<typename T, typename... S> void print(T && x, S&&... y) {cout << x << ' ';print(y...);}
template<typename T> istream& operator >> (istream& i, vector<T> &vec){for(auto &x: vec) i >> x; return i;}
vvi read_graph(int n, int m, int base=1){
vvi adj(n);
for(int i=0,u,v; i<m; ++i){
cin >> u >> v,u-=base,v-=base;
adj[u].pb(v),adj[v].pb(u);
}
return adj;
}
vvi read_tree(int n, int base=1){return read_graph(n,n-1,base);}
template<typename T, typename S> pair<T,S> operator + (const pair<T,S> &a, const pair<T,S> &b){return {a.first+b.first,a.second+b.second};}
template<typename T> constexpr T inf=0;
template<> constexpr int inf<int> = 0x3f3f3f3f;
template<> constexpr ll inf<ll> = 0x3f3f3f3f3f3f3f3f;
template<typename T> vector<T> operator += (vector<T> &a, int val){for(auto &i: a) i+=val; return a;}
template<typename T> T isqrt(const T &x){T y=sqrt(x+2); while(y*y>x) y--; return y;}
#define ykh mt19937 rng(chrono::steady_clock::now().time_since_epoch().count())
#include <utility>
namespace atcoder {
namespace internal {
// @param m `1 <= m`
// @return x mod m
constexpr long long safe_mod(long long x, long long m) {
x %= m;
if (x < 0) x += m;
return x;
}
// Fast modular multiplication by barrett reduction
// Reference: https://en.wikipedia.org/wiki/Barrett_reduction
// NOTE: reconsider after Ice Lake
struct barrett {
unsigned int _m;
unsigned long long im;
// @param m `1 <= m < 2^31`
barrett(unsigned int m) : _m(m), im((unsigned long long)(-1) / m + 1) {}
// @return m
unsigned int umod() const { return _m; }
// @param a `0 <= a < m`
// @param b `0 <= b < m`
// @return `a * b % m`
unsigned int mul(unsigned int a, unsigned int b) const {
// [1] m = 1
// a = b = im = 0, so okay
// [2] m >= 2
// im = ceil(2^64 / m)
// -> im * m = 2^64 + r (0 <= r < m)
// let z = a*b = c*m + d (0 <= c, d < m)
// a*b * im = (c*m + d) * im = c*(im*m) + d*im = c*2^64 + c*r + d*im
// c*r + d*im < m * m + m * im < m * m + 2^64 + m <= 2^64 + m * (m + 1) < 2^64 * 2
// ((ab * im) >> 64) == c or c + 1
unsigned long long z = a;
z *= b;
#ifdef _MSC_VER
unsigned long long x;
_umul128(z, im, &x);
#else
unsigned long long x =
(unsigned long long)(((unsigned __int128)(z)*im) >> 64);
#endif
unsigned int v = (unsigned int)(z - x * _m);
if (_m <= v) v += _m;
return v;
}
};
// @param n `0 <= n`
// @param m `1 <= m`
// @return `(x ** n) % m`
constexpr long long pow_mod_constexpr(long long x, long long n, int m) {
if (m == 1) return 0;
unsigned int _m = (unsigned int)(m);
unsigned long long r = 1;
unsigned long long y = safe_mod(x, m);
while (n) {
if (n & 1) r = (r * y) % _m;
y = (y * y) % _m;
n >>= 1;
}
return r;
}
// Reference:
// M. Forisek and J. Jancina,
// Fast Primality Testing for Integers That Fit into a Machine Word
// @param n `0 <= n`
constexpr bool is_prime_constexpr(int n) {
if (n <= 1) return false;
if (n == 2 || n == 7 || n == 61) return true;
if (n % 2 == 0) return false;
long long d = n - 1;
while (d % 2 == 0) d /= 2;
constexpr long long bases[3] = {2, 7, 61};
for (long long a : bases) {
long long t = d;
long long y = pow_mod_constexpr(a, t, n);
while (t != n - 1 && y != 1 && y != n - 1) {
y = y * y % n;
t <<= 1;
}
if (y != n - 1 && t % 2 == 0) {
return false;
}
}
return true;
}
template <int n> constexpr bool is_prime = is_prime_constexpr(n);
// @param b `1 <= b`
// @return pair(g, x) s.t. g = gcd(a, b), xa = g (mod b), 0 <= x < b/g
constexpr std::pair<long long, long long> inv_gcd(long long a, long long b) {
a = safe_mod(a, b);
if (a == 0) return {b, 0};
// Contracts:
// [1] s - m0 * a = 0 (mod b)
// [2] t - m1 * a = 0 (mod b)
// [3] s * |m1| + t * |m0| <= b
long long s = b, t = a;
long long m0 = 0, m1 = 1;
while (t) {
long long u = s / t;
s -= t * u;
m0 -= m1 * u; // |m1 * u| <= |m1| * s <= b
// [3]:
// (s - t * u) * |m1| + t * |m0 - m1 * u|
// <= s * |m1| - t * u * |m1| + t * (|m0| + |m1| * u)
// = s * |m1| + t * |m0| <= b
auto tmp = s;
s = t;
t = tmp;
tmp = m0;
m0 = m1;
m1 = tmp;
}
// by [3]: |m0| <= b/g
// by g != b: |m0| < b/g
if (m0 < 0) m0 += b / s;
return {s, m0};
}
// Compile time primitive root
// @param m must be prime
// @return primitive root (and minimum in now)
constexpr int primitive_root_constexpr(int m) {
if (m == 2) return 1;
if (m == 167772161) return 3;
if (m == 469762049) return 3;
if (m == 754974721) return 11;
if (m == 998244353) return 3;
int divs[20] = {};
divs[0] = 2;
int cnt = 1;
int x = (m - 1) / 2;
while (x % 2 == 0) x /= 2;
for (int i = 3; (long long)(i)*i <= x; i += 2) {
if (x % i == 0) {
divs[cnt++] = i;
while (x % i == 0) {
x /= i;
}
}
}
if (x > 1) {
divs[cnt++] = x;
}
for (int g = 2;; g++) {
bool ok = true;
for (int i = 0; i < cnt; i++) {
if (pow_mod_constexpr(g, (m - 1) / divs[i], m) == 1) {
ok = false;
break;
}
}
if (ok) return g;
}
}
template <int m> constexpr int primitive_root = primitive_root_constexpr(m);
} // namespace internal
} // namespace atcoder
#include <cassert>
#include <numeric>
#include <type_traits>
namespace atcoder {
namespace internal {
#ifndef _MSC_VER
template <class T>
using is_signed_int128 =
typename std::conditional<std::is_same<T, __int128_t>::value ||
std::is_same<T, __int128>::value,
std::true_type,
std::false_type>::type;
template <class T>
using is_unsigned_int128 =
typename std::conditional<std::is_same<T, __uint128_t>::value ||
std::is_same<T, unsigned __int128>::value,
std::true_type,
std::false_type>::type;
template <class T>
using make_unsigned_int128 =
typename std::conditional<std::is_same<T, __int128_t>::value,
__uint128_t,
unsigned __int128>;
template <class T>
using is_integral = typename std::conditional<std::is_integral<T>::value ||
is_signed_int128<T>::value ||
is_unsigned_int128<T>::value,
std::true_type,
std::false_type>::type;
template <class T>
using is_signed_int = typename std::conditional<(is_integral<T>::value &&
std::is_signed<T>::value) ||
is_signed_int128<T>::value,
std::true_type,
std::false_type>::type;
template <class T>
using is_unsigned_int =
typename std::conditional<(is_integral<T>::value &&
std::is_unsigned<T>::value) ||
is_unsigned_int128<T>::value,
std::true_type,
std::false_type>::type;
template <class T>
using to_unsigned = typename std::conditional<
is_signed_int128<T>::value,
make_unsigned_int128<T>,
typename std::conditional<std::is_signed<T>::value,
std::make_unsigned<T>,
std::common_type<T>>::type>::type;
#else
template <class T> using is_integral = typename std::is_integral<T>;
template <class T>
using is_signed_int =
typename std::conditional<is_integral<T>::value && std::is_signed<T>::value,
std::true_type,
std::false_type>::type;
template <class T>
using is_unsigned_int =
typename std::conditional<is_integral<T>::value &&
std::is_unsigned<T>::value,
std::true_type,
std::false_type>::type;
template <class T>
using to_unsigned = typename std::conditional<is_signed_int<T>::value,
std::make_unsigned<T>,
std::common_type<T>>::type;
#endif
template <class T>
using is_signed_int_t = std::enable_if_t<is_signed_int<T>::value>;
template <class T>
using is_unsigned_int_t = std::enable_if_t<is_unsigned_int<T>::value>;
template <class T> using to_unsigned_t = typename to_unsigned<T>::type;
} // namespace internal
} // namespace atcoder
#include <cassert>
#include <numeric>
#include <type_traits>
#ifdef _MSC_VER
#include <intrin.h>
#endif
namespace atcoder {
namespace internal {
struct modint_base {};
struct static_modint_base : modint_base {};
template <class T> using is_modint = std::is_base_of<modint_base, T>;
template <class T> using is_modint_t = std::enable_if_t<is_modint<T>::value>;
} // namespace internal
template <int m, std::enable_if_t<(1 <= m)>* = nullptr>
struct static_modint : internal::static_modint_base {
using mint = static_modint;
public:
static constexpr int mod() { return m; }
static mint raw(int v) {
mint x;
x._v = v;
return x;
}
static_modint() : _v(0) {}
template <class T, internal::is_signed_int_t<T>* = nullptr>
static_modint(T v) {
long long x = (long long)(v % (long long)(umod()));
if (x < 0) x += umod();
_v = (unsigned int)(x);
}
template <class T, internal::is_unsigned_int_t<T>* = nullptr>
static_modint(T v) {
_v = (unsigned int)(v % umod());
}
static_modint(bool v) { _v = ((unsigned int)(v) % umod()); }
unsigned int val() const { return _v; }
mint& operator++() {
_v++;
if (_v == umod()) _v = 0;
return *this;
}
mint& operator--() {
if (_v == 0) _v = umod();
_v--;
return *this;
}
mint operator++(int) {
mint result = *this;
++*this;
return result;
}
mint operator--(int) {
mint result = *this;
--*this;
return result;
}
mint& operator+=(const mint& rhs) {
_v += rhs._v;
if (_v >= umod()) _v -= umod();
return *this;
}
mint& operator-=(const mint& rhs) {
_v -= rhs._v;
if (_v >= umod()) _v += umod();
return *this;
}
mint& operator*=(const mint& rhs) {
unsigned long long z = _v;
z *= rhs._v;
_v = (unsigned int)(z % umod());
return *this;
}
mint& operator/=(const mint& rhs) { return *this = *this * rhs.inv(); }
mint operator+() const { return *this; }
mint operator-() const { return mint() - *this; }
mint pow(long long n) const {
assert(0 <= n);
mint x = *this, r = 1;
while (n) {
if (n & 1) r *= x;
x *= x;
n >>= 1;
}
return r;
}
mint inv() const {
if (prime) {
assert(_v);
return pow(umod() - 2);
} else {
auto eg = internal::inv_gcd(_v, m);
assert(eg.first == 1);
return eg.second;
}
}
friend mint operator+(const mint& lhs, const mint& rhs) {
return mint(lhs) += rhs;
}
friend mint operator-(const mint& lhs, const mint& rhs) {
return mint(lhs) -= rhs;
}
friend mint operator*(const mint& lhs, const mint& rhs) {
return mint(lhs) *= rhs;
}
friend mint operator/(const mint& lhs, const mint& rhs) {
return mint(lhs) /= rhs;
}
friend bool operator==(const mint& lhs, const mint& rhs) {
return lhs._v == rhs._v;
}
friend bool operator!=(const mint& lhs, const mint& rhs) {
return lhs._v != rhs._v;
}
private:
unsigned int _v;
static constexpr unsigned int umod() { return m; }
static constexpr bool prime = internal::is_prime<m>;
};
template <int id> struct dynamic_modint : internal::modint_base {
using mint = dynamic_modint;
public:
static int mod() { return (int)(bt.umod()); }
static void set_mod(int m) {
assert(1 <= m);
bt = internal::barrett(m);
}
static mint raw(int v) {
mint x;
x._v = v;
return x;
}
dynamic_modint() : _v(0) {}
template <class T, internal::is_signed_int_t<T>* = nullptr>
dynamic_modint(T v) {
long long x = (long long)(v % (long long)(mod()));
if (x < 0) x += mod();
_v = (unsigned int)(x);
}
template <class T, internal::is_unsigned_int_t<T>* = nullptr>
dynamic_modint(T v) {
_v = (unsigned int)(v % mod());
}
dynamic_modint(bool v) { _v = ((unsigned int)(v) % mod()); }
unsigned int val() const { return _v; }
mint& operator++() {
_v++;
if (_v == umod()) _v = 0;
return *this;
}
mint& operator--() {
if (_v == 0) _v = umod();
_v--;
return *this;
}
mint operator++(int) {
mint result = *this;
++*this;
return result;
}
mint operator--(int) {
mint result = *this;
--*this;
return result;
}
mint& operator+=(const mint& rhs) {
_v += rhs._v;
if (_v >= umod()) _v -= umod();
return *this;
}
mint& operator-=(const mint& rhs) {
_v += mod() - rhs._v;
if (_v >= umod()) _v -= umod();
return *this;
}
mint& operator*=(const mint& rhs) {
_v = bt.mul(_v, rhs._v);
return *this;
}
mint& operator/=(const mint& rhs) { return *this = *this * rhs.inv(); }
mint operator+() const { return *this; }
mint operator-() const { return mint() - *this; }
mint pow(long long n) const {
assert(0 <= n);
mint x = *this, r = 1;
while (n) {
if (n & 1) r *= x;
x *= x;
n >>= 1;
}
return r;
}
mint inv() const {
auto eg = internal::inv_gcd(_v, mod());
assert(eg.first == 1);
return eg.second;
}
friend mint operator+(const mint& lhs, const mint& rhs) {
return mint(lhs) += rhs;
}
friend mint operator-(const mint& lhs, const mint& rhs) {
return mint(lhs) -= rhs;
}
friend mint operator*(const mint& lhs, const mint& rhs) {
return mint(lhs) *= rhs;
}
friend mint operator/(const mint& lhs, const mint& rhs) {
return mint(lhs) /= rhs;
}
friend bool operator==(const mint& lhs, const mint& rhs) {
return lhs._v == rhs._v;
}
friend bool operator!=(const mint& lhs, const mint& rhs) {
return lhs._v != rhs._v;
}
private:
unsigned int _v;
static internal::barrett bt;
static unsigned int umod() { return bt.umod(); }
};
template <int id> internal::barrett dynamic_modint<id>::bt = 998244353;
using modint998244353 = static_modint<998244353>;
using modint1000000007 = static_modint<1000000007>;
using modint = dynamic_modint<-1>;
namespace internal {
template <class T>
using is_static_modint = std::is_base_of<internal::static_modint_base, T>;
template <class T>
using is_static_modint_t = std::enable_if_t<is_static_modint<T>::value>;
template <class> struct is_dynamic_modint : public std::false_type {};
template <int id>
struct is_dynamic_modint<dynamic_modint<id>> : public std::true_type {};
template <class T>
using is_dynamic_modint_t = std::enable_if_t<is_dynamic_modint<T>::value>;
} // namespace internal
} // namespace atcoder
#include <algorithm>
#include <array>
#ifdef _MSC_VER
#include <intrin.h>
#endif
namespace atcoder {
namespace internal {
// @param n `0 <= n`
// @return minimum non-negative `x` s.t. `n <= 2**x`
int ceil_pow2(int n) {
int x = 0;
while ((1U << x) < (unsigned int)(n)) x++;
return x;
}
// @param n `1 <= n`
// @return minimum non-negative `x` s.t. `(n & (1 << x)) != 0`
int bsf(unsigned int n) {
#ifdef _MSC_VER
unsigned long index;
_BitScanForward(&index, n);
return index;
#else
return __builtin_ctz(n);
#endif
}
} // namespace internal
} // namespace atcoder
#include <cassert>
#include <type_traits>
#include <vector>
namespace atcoder {
namespace internal {
template <class mint, internal::is_static_modint_t<mint>* = nullptr>
void butterfly(std::vector<mint>& a) {
static constexpr int g = internal::primitive_root<mint::mod()>;
int n = int(a.size());
int h = internal::ceil_pow2(n);
static bool first = true;
static mint sum_e[30]; // sum_e[i] = ies[0] * ... * ies[i - 1] * es[i]
if (first) {
first = false;
mint es[30], ies[30]; // es[i]^(2^(2+i)) == 1
int cnt2 = bsf(mint::mod() - 1);
mint e = mint(g).pow((mint::mod() - 1) >> cnt2), ie = e.inv();
for (int i = cnt2; i >= 2; i--) {
// e^(2^i) == 1
es[i - 2] = e;
ies[i - 2] = ie;
e *= e;
ie *= ie;
}
mint now = 1;
for (int i = 0; i <= cnt2 - 2; i++) {
sum_e[i] = es[i] * now;
now *= ies[i];
}
}
for (int ph = 1; ph <= h; ph++) {
int w = 1 << (ph - 1), p = 1 << (h - ph);
mint now = 1;
for (int s = 0; s < w; s++) {
int offset = s << (h - ph + 1);
for (int i = 0; i < p; i++) {
auto l = a[i + offset];
auto r = a[i + offset + p] * now;
a[i + offset] = l + r;
a[i + offset + p] = l - r;
}
now *= sum_e[bsf(~(unsigned int)(s))];
}
}
}
template <class mint, internal::is_static_modint_t<mint>* = nullptr>
void butterfly_inv(std::vector<mint>& a) {
static constexpr int g = internal::primitive_root<mint::mod()>;
int n = int(a.size());
int h = internal::ceil_pow2(n);
static bool first = true;
static mint sum_ie[30]; // sum_ie[i] = es[0] * ... * es[i - 1] * ies[i]
if (first) {
first = false;
mint es[30], ies[30]; // es[i]^(2^(2+i)) == 1
int cnt2 = bsf(mint::mod() - 1);
mint e = mint(g).pow((mint::mod() - 1) >> cnt2), ie = e.inv();
for (int i = cnt2; i >= 2; i--) {
// e^(2^i) == 1
es[i - 2] = e;
ies[i - 2] = ie;
e *= e;
ie *= ie;
}
mint now = 1;
for (int i = 0; i <= cnt2 - 2; i++) {
sum_ie[i] = ies[i] * now;
now *= es[i];
}
}
for (int ph = h; ph >= 1; ph--) {
int w = 1 << (ph - 1), p = 1 << (h - ph);
mint inow = 1;
for (int s = 0; s < w; s++) {
int offset = s << (h - ph + 1);
for (int i = 0; i < p; i++) {
auto l = a[i + offset];
auto r = a[i + offset + p];
a[i + offset] = l + r;
a[i + offset + p] =
(unsigned long long)(mint::mod() + l.val() - r.val()) *
inow.val();
}
inow *= sum_ie[bsf(~(unsigned int)(s))];
}
}
}
} // namespace internal
template <class mint, internal::is_static_modint_t<mint>* = nullptr>
std::vector<mint> convolution(std::vector<mint> a, std::vector<mint> b) {
int n = int(a.size()), m = int(b.size());
if (!n || !m) return {};
if (std::min(n, m) <= 60) {
if (n < m) {
std::swap(n, m);
std::swap(a, b);
}
std::vector<mint> ans(n + m - 1);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
ans[i + j] += a[i] * b[j];
}
}
return ans;
}
int z = 1 << internal::ceil_pow2(n + m - 1);
a.resize(z);
internal::butterfly(a);
b.resize(z);
internal::butterfly(b);
for (int i = 0; i < z; i++) {
a[i] *= b[i];
}
internal::butterfly_inv(a);
a.resize(n + m - 1);
mint iz = mint(z).inv();
for (int i = 0; i < n + m - 1; i++) a[i] *= iz;
return a;
}
template <unsigned int mod = 998244353,
class T,
std::enable_if_t<internal::is_integral<T>::value>* = nullptr>
std::vector<T> convolution(const std::vector<T>& a, const std::vector<T>& b) {
int n = int(a.size()), m = int(b.size());
if (!n || !m) return {};
using mint = static_modint<mod>;
std::vector<mint> a2(n), b2(m);
for (int i = 0; i < n; i++) {
a2[i] = mint(a[i]);
}
for (int i = 0; i < m; i++) {
b2[i] = mint(b[i]);
}
auto c2 = convolution(move(a2), move(b2));
std::vector<T> c(n + m - 1);
for (int i = 0; i < n + m - 1; i++) {
c[i] = c2[i].val();
}
return c;
}
std::vector<long long> convolution_ll(const std::vector<long long>& a,
const std::vector<long long>& b) {
int n = int(a.size()), m = int(b.size());
if (!n || !m) return {};
static constexpr unsigned long long MOD1 = 754974721; // 2^24
static constexpr unsigned long long MOD2 = 167772161; // 2^25
static constexpr unsigned long long MOD3 = 469762049; // 2^26
static constexpr unsigned long long M2M3 = MOD2 * MOD3;
static constexpr unsigned long long M1M3 = MOD1 * MOD3;
static constexpr unsigned long long M1M2 = MOD1 * MOD2;
static constexpr unsigned long long M1M2M3 = MOD1 * MOD2 * MOD3;
static constexpr unsigned long long i1 =
internal::inv_gcd(MOD2 * MOD3, MOD1).second;
static constexpr unsigned long long i2 =
internal::inv_gcd(MOD1 * MOD3, MOD2).second;
static constexpr unsigned long long i3 =
internal::inv_gcd(MOD1 * MOD2, MOD3).second;
auto c1 = convolution<MOD1>(a, b);
auto c2 = convolution<MOD2>(a, b);
auto c3 = convolution<MOD3>(a, b);
std::vector<long long> c(n + m - 1);
for (int i = 0; i < n + m - 1; i++) {
unsigned long long x = 0;
x += (c1[i] * i1) % MOD1 * M2M3;
x += (c2[i] * i2) % MOD2 * M1M3;
x += (c3[i] * i3) % MOD3 * M1M2;
// B = 2^63, -B <= x, r(real value) < B
// (x, x - M, x - 2M, or x - 3M) = r (mod 2B)
// r = c1[i] (mod MOD1)
// focus on MOD1
// r = x, x - M', x - 2M', x - 3M' (M' = M % 2^64) (mod 2B)
// r = x,
// x - M' + (0 or 2B),
// x - 2M' + (0, 2B or 4B),
// x - 3M' + (0, 2B, 4B or 6B) (without mod!)
// (r - x) = 0, (0)
// - M' + (0 or 2B), (1)
// -2M' + (0 or 2B or 4B), (2)
// -3M' + (0 or 2B or 4B or 6B) (3) (mod MOD1)
// we checked that
// ((1) mod MOD1) mod 5 = 2
// ((2) mod MOD1) mod 5 = 3
// ((3) mod MOD1) mod 5 = 4
long long diff =
c1[i] - internal::safe_mod((long long)(x), (long long)(MOD1));
if (diff < 0) diff += MOD1;
static constexpr unsigned long long offset[5] = {
0, 0, M1M2M3, 2 * M1M2M3, 3 * M1M2M3};
x -= offset[diff % 5];
c[i] = x;
}
return c;
}
} // namespace atcoder
using namespace atcoder;
using mint=modint998244353;
//using mint=modint1000000007;
template<int mod>
struct nCr{
vector<static_modint<mod>> fac,inv,ifac;
void calc(int n){
fac.resize(n+1),inv.resize(n+1),ifac.resize(n+1);
fac[0]=inv[1]=ifac[0]=1;
for(int i=1; i<=n; ++i) fac[i]=fac[i-1]*static_modint<mod>::raw(i);
for(int i=2; i<=n; ++i) inv[i]=inv[mod%i]*static_modint<mod>::raw(mod-mod/i);
for(int i=1; i<=n; ++i) ifac[i]=ifac[i-1]*inv[i];
}
static_modint<mod> C(int n, int m){
if(m<0||m>n) return 0;
return fac[n]*ifac[m]*ifac[n-m];
}
};
nCr<998244353> de;
void ahcorz(){
// (a_i - j)! / (a_i - i)! (a_i = a_j)
// (a_i - j - 1)! / (a_i - i)! * (i - j) (a_i != a_j)
int n; cin >> n;
de.calc(n+1);
vi a; a.pb(0);
rep(n){
int x; cin >> x;
a.pb(max(a.back(),x));
}
vc<mint> dp(n+1),aux(n+1);
auto solve=[&](auto &self, int l, int r) -> void{
if(l+1==r){
if(l==0) dp[l]=-1;
else dp[l]+=aux[l]*l;
dp[l]*=de.ifac[a[l]-l];
return;
}
int mid=l+r>>1;
self(self,l,mid);
if(a[mid]==a[mid-1]){
int x=mid-1,y=mid;
while(x-1>=l&&a[x-1]==a[mid]) x--;
while(y+1<r&&a[y+1]==a[mid]) y++;
mint tot,tot1,tot2;
rep(i,x,mid) tot+=dp[i]*de.fac[a[mid]-i],tot1+=dp[i]*de.fac[a[mid]-i-1],tot2+=dp[i]*de.fac[a[mid]-i-1]*i;
rep(i,mid,y+1) dp[i]-=tot-(tot1*i-tot2);
}
vc<mint> vec;
rep(i,a[mid]-mid,a[r-1]-(l+1)+1) vec.pb(de.fac[i]);
vc<mint> vec1,vec2;
rep(i,l,mid) vec1.pb(dp[i]),vec2.pb(dp[i]*i);
auto res1=convolution(vec,vec1),res2=convolution(vec,vec2);
int base=a[mid]-mid+l+1;
rep(i,mid,r) if(a[i]-base>=0&&a[i]-base<sz(res1)) aux[i]-=res1[a[i]-base],dp[i]+=res2[a[i]-base];
self(self,mid,r);
};
solve(solve,0,n+1);
print(dp[n].val());
}
signed main(){
ios_base::sync_with_stdio(0),cin.tie(0);
cout << fixed << setprecision(20);
int t=1;
cin >> t;
while(t--) ahcorz();
}
D1F — Grand Finale: Circles
Idea : chromate00
UPD: The TL was a bit too loose, and unintended solutions with $$$\mathcal{O}(n \log^2 (1/\epsilon))$$$ complexity passed during the round. For the sake of the problem itself, I suggest that you try to solve assuming a $$$1$$$ second time limit.
For a given center coordinate $$$(x,y)$$$, we can model the objective function $$$r=f(x,y)$$$ to maximize as follows.
Unable to parse markup [type=CF_MATHJAX]
Formally, this can be modeled as follows:
This is a second order cone program. Generally, this is not as simple to solve as linear or quadratic programs. There are multiple solvers out there, but all of them are either commercial or simply unfit for use on Codeforces. And even if we use general approaches to second order cone programming, their time complexity is at least $$$\mathcal{O}(n^{3.5})$$$, so they cannot work. Almost all general approaches to convex programming do not help very much for this task also, because of the following reasons.
Gradient Descent cannot work in this task. The objective function is not smooth.
Coordinate Descent also cannot work in this task for the same reason, and it is not hard to find a countercase.
Subgradient methods can solve this task, but they take $$$\mathcal{O}(1/\epsilon^2)$$$ iterations to converge. This is a very big dependency on the precision, so they take too much time.
We do not expect anyone to write Adaptive Coordinate Descent during contest time, but we still tested the PRAXIS algorithm and checked that it does not pass.
Using nested ternary searches does not help very much. The time complexity will be $$$\mathcal{O}(n \log^2 (1/\epsilon))$$$, but the constants are large due to multiple function calls and floating point operations.
Heuristics such as the Nelder-Mead method are not proven to converge. In many cases we found it not converging successfully.
In the editorial, we will explain a solution of expected $$$\mathcal{O}(n)$$$ time complexity, with constants depending on the number of dimensions (which is $$$2$$$ in our case).
First, we observe that any answer can be described as a "basis" of at most $$$3$$$ selected circles. For $$$k=0,1,2,3$$$, the basis is as follows.
- Case 1: $$$k=0$$$
This is the case of no circles, which can be regarded as an "identity element" of bases. Some very huge circle that will enclose any given circle, for example the circle with $$$10^{18}$$$ as radius and $$$(0,0)$$$ as center, can represent this case.
- Case 2: $$$k=1$$$
This is the case of a single circle. The circle that represents this case is the one selected circle.
- Case 3: $$$k=2$$$
This is the case of two circles, for which the basis is the largest circle in the intersection of two circles. We can find this by choosing the center as the midpoint of the two points $$$A$$$ and $$$B$$$, where $$$A$$$ and $$$B$$$ are the points where the line segment between circle centers and the circle itself intersect.
- Case 4: $$$k=3$$$
This is the case of three circles, and the most tricky of all four cases. It can be found as one solution to the following system of quadratic equations:
This can be solved algebraically. If you are used to solving geometry problems in Olympiads, you may know the ''Problem of Apollonius''. This is one special case of the problem, which is not very often mentioned because often the three circles do not intersect with each other (thus most of the time one solution for $$$r$$$ must be negative). Or if one does not know the problem, they can find that the locus of the circle center that meets with two circle edges (as in Case 3) is a conic section, precisely one side of a pair of hyperbola. By finding the intersections of two hyperbola, one can find the center of this circle. Thus, this circle can be found in $$$\mathcal{O}(1)$$$ time, with constants based on number of dimensions.
By the system of quadratic equations stated above, we see that there are at most $$$2$$$ solutions. It is sufficient to take the one that happens to be inside the intersection. (If there are two such solutions, take the larger one. For the current version of the data this check is not necessary, but it does not hurt to try.) Thus, for some $$$n>3$$$, the bases can be represented with some $$$k \le 3$$$ circles.
Do note that, already, we have an $$$\mathcal{O}(n^3)$$$ solution based on this. We enumerate all possible bases, and find the smallest one out of them (since that one will be the one that satisfies the conditions).
Now, for some basis circle $$$(x,y,r)$$$, we can check whether some given circle $$$(x_i,y_i,r_i)$$$ is "violated" by this basis (i.e. this basis is not inside this circle) in $$$\mathcal{O}(1)$$$ by comparing the distance. We take an incremental approach. We add circles to the basis one by one, up to $$$3$$$ circles. We choose to change the basis if only the next added circle is violated by the current basis. Of course, still this takes $$$\mathcal{O}(n^3)$$$ time, and sorting the circles based on any argument will not help anyways.
However, adding the circles in random order will make it only take expected $$$\mathcal{O}(n)$$$ time. This can be analyzed by the probability that a new basis will be added. The precise analysis for the time complexity is left as a practice for the reader.
If you have seen the minimum enclosing circle problem, the Welzl's algorithm to solve that precise problem will seem very similar to this. In fact, the suggested algorithm itself is not very different from Welzl's algorithm. If you want, though, you may take an iterative approach instead of modifying Welzl's algorithm. Using three nested loops will do.
There is only two issues left. The first is the issue of numerical instability. Sometimes, due to numerical instability, the algorithm will return a NaN value. It is not that hard to solve, we can simply shuffle again and rerun the algorithm. The given time limit will be sufficient for doing this unless the constant is too big. The second is more tricky, and it is about hacks.
If you use a fixed seed for randomization (or time-based seeds to some extent), someone may hack you by adding an adversarial test case which makes the time complexity explode back to $$$\mathcal{O}(n^3)$$$. This is very bad. How do we solve this? To intervent this, we will make the algorithm halt when the number of iterations exceed a certain limit. Formally, let us choose a constant $$$c$$$, and the algorithm will halt and rerun when the number of iterations exceeds $$$c \cdot n$$$. Then, if the probability of the algorithm successfully running in this number of iterations is $$$p$$$, the expected number of reruns needed is $$$\mathcal{O}(1/p)$$$, and hacking is much harder. The algorithm will successfully find the solution in $$$\mathcal{O}((c/p) \cdot n)$$$ time. Of course, the probability $$$p$$$ depends on $$$c$$$, and you must tune the value as needed. Empirically $$$c=30$$$ runs very well, almost always taking no longer than $$$0.4$$$ seconds under proper optimizations, and $$$1.5$$$ seconds without.
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
using lf=long double;
using pt=pair<lf,lf>;
lf& real(pt& p){return p.first;}
lf& imag(pt& p){return p.second;}
pt midp(pt a,pt b){return pt{(real(a)+real(b))/2,(imag(a)+imag(b))/2};}
pt addi(pt a,pt b){return pt{(real(a)+real(b)),(imag(a)+imag(b))};}
pt subt(pt a,pt b){return pt{(real(a)-real(b)),(imag(a)-imag(b))};}
pt mult(pt a,lf b){return pt{real(a)*b,imag(a)*b};}
lf abs(pt a){return sqrtl(powl(real(a),2)+powl(imag(a),2));}
lf dist(pt a,pt b){return sqrtl(powl(real(a)-real(b),2)+powl(imag(a)-imag(b),2));}
struct circ{pt p;lf r;};
const lf inf=1e18;
circ basis0(){return {pt{0,0},inf};}
circ basis1(circ a){return a;}
circ basis2(circ a,circ b)
{
pt aa=a.p,bb=b.p;
pt ab=subt(bb,aa),ba=subt(aa,bb);
lf aab=abs(ab),aba=abs(ba);
real(ab)/=aab;
imag(ab)/=aab;
real(ba)/=aba;
imag(ba)/=aba;
pt ar=addi(aa,mult(ab,a.r)),br=addi(bb,mult(ba,b.r));
return {midp(ar,br),dist(ar,br)/2.0L};
}
circ basis3(circ a,circ b,circ c)
{
lf x1=real(a.p),y1=imag(a.p),r1=a.r;
lf x2=real(b.p),y2=imag(b.p),r2=b.r;
lf x3=real(c.p),y3=imag(c.p),r3=c.r;
lf a2=x1-x2,a3=x1-x3,b2=y1-y2,b3=y1-y3,c2=r2-r1,c3=r3-r1;
lf d1=x1*x1+y1*y1-r1*r1,d2=d1-x2*x2-y2*y2+r2*r2,d3=d1-x3*x3-y3*y3+r3*r3;
lf ab=a3*b2-a2*b3;
lf xa=(b2*d3-b3*d2)/(ab*2)-x1;
lf xb=(b3*c2-b2*c3)/ab;
lf ya=(a3*d2-a2*d3)/(ab*2)-y1;
lf yb=(a2*c3-a3*c2)/ab;
lf A=xb*xb+yb*yb-1;
lf B=2*(r1+xa*xb+ya*yb);
lf C=xa*xa+ya*ya-r1*r1;
lf r=-(A?(B-sqrtl(B*B-4*A*C))/(2*A):C/B);
return {pt{x1+xa+xb*r,y1+ya+yb*r},r};
}
bool viol(circ p,circ a)
{
return a.r<p.r+dist(a.p,p.p);
}
circ solve(vector<circ>&v)
{
lf _nan=nan("aaa");
mt19937_64 mt(1999999);
//shuffle(begin(v),end(v),mt);
vector<circ>basis;
auto trivial=[&]()
{
if(size(basis)==0)return basis0();
if(size(basis)==1)return basis[0];
if(size(basis)==2)return basis2(basis[0],basis[1]);
return basis3(basis[0],basis[1],basis[2]);
};
int counter=0;
auto rec=[&](auto rec,int n)->circ
{
if(n==0||size(basis)==3)return trivial();
counter++;
if(counter>30*size(v))return {pt{0,0},_nan};
auto c=rec(rec,n-1);
auto p=v[n-1];
if(!viol(c,p)||isnan(c.r))return c;
basis.push_back(p);
c=rec(rec,n-1);
basis.pop_back();
return c;
};
auto c=rec(rec,size(v));
while(isnan(c.r))
{
counter=0;
shuffle(begin(v),end(v),mt);
c=rec(rec,size(v));
}
return c;
}
int main()
{
cin.tie(0)->sync_with_stdio(0);
int n;cin>>n;
vector<circ>v(n);
for(auto&[p,r]:v)
{
ll x,y,rr;cin>>x>>y>>rr;
p={x,y};r=rr;
}
auto ans=solve(v);
cout<<setprecision(16)<<fixed<<real(ans.p)<<" "<<imag(ans.p)<<" "<<ans.r<<"\n";
}











fast editorial
++ fast system testing
It seems like it's forzen right now...
Why it,s frozen? Do you have any idea ?
kindly help me in this DIV2 -B
int n;
void solve(){
cin>>n;
string u, d; cin>>u>>d;
string s = u[0] + d;
string c=s;
int cnt=0;
for(int i=0;i<n;i++){
}
cout<<c<<'\n'<<cnt<<'\n'; }
It is giving TLE -- but it is running in O(n) time
哥们,string 比较大小时间复杂度很高,每次比较大小都是O(n),因此整个时间复杂度是O(t*n^2),
so , This code may exceed the time limit
yeah. I got the same problem, so I had to switch the solution entirely. Luckily, I was able to solve it.
What's this, 混合双语解答问题吗,I don't think anyone can understand this :(
你不就understand了嘛qwq
If in terms of string comparison, you can use a hash plus binary search, binary search to find the longest length of the same prefix, the next position is the first different position, and then compare the characters at that position, this only requires O(logn), preprocessing requires O(n). By machine translation, there may be errors,you can continue to ask me.
Fast Editoral
Fast editorial! Never seen one posted so fast after a contest.
if we don't mention um_nik's editorial
Haven't tried his rounds yet
It's a joke about last div3 https://codeforces.me/blog/entry/126461
It was this contest that he accidentally published his screencast 40 minutes before the end of the contest.
Great round ! I really enjoyed solving problem B and C. Congrats to the authors !
I don't know if I should be happy that I solved div1A+B fast or sad that I spent over an hour on C and didn't get it!!
Either way, thank you for the amazing contest! I've just got to read the editorial for C now ^_^
fast editorial
Interesting problems, but don’t you think that the difficulty of Div.1 is A > B > C?
For problem F I didn't have enough braincells for solving the k=3 case so I simply used the idea from Radewoosh's blog number 5 https://codeforces.me/blog/entry/61710 (binary search for the radius + the blog for finding the intersection after shrinking circles + using golden-ratio search to optimize).
Also didn't realize the k=4 case apparently didn't exist, hopefully it's not FST due to time seed.
Edit: chromate00 idk if it was you that put that note for F, but doing binary search and ternary search while doing the rest as in the editorial seems fine to me. The expected number of retries in the algorithm is O(log^3N) I'm pretty sure, so in the end it's something like O(log^3N * log^2precision) + O(N).
It should be fine if you do the rest of the blog along with one binary search. I haven't tested with two, though. The $$$\mathcal{O}(n\log^2(1/\epsilon))$$$ I was referring to was the nested golden section search where the $$$\mathcal{O}(n)$$$ is simply from calling the objective function. Do note though, that we do have a tester solution with $$$\mathcal{O}(n\log^2(1/\epsilon))$$$ complexity that passes in ~800ms.
hmm I just submitted $$$O(n\log^2(1/\epsilon))$$$ and it's faster than everyone else's solutions ...
I believe it is one of the $$$\mathcal{O}(n \log^2(1/\epsilon))$$$ we intended to allow. Most of the $$$\mathcal{O}(n \log^2(1/\epsilon))$$$ I meant to block were the ones that do ternary search on both $$$x$$$ and $$$y$$$, to maximize $$$r$$$. In the meantime, a tester's solution using binary search on $$$r$$$ with a clever check function passes in about 800ms.
Ok.
Ok. Btw, I tried uncommenting the first random shuffle in the model sol and resubmitting with different random seeds, and they all gave different outputs. So I assume the model sol is not correct.
Example code (only difference is the seed):
AC: 249100355
WA:
249108458
249116485
249116654
As far as I believe, the issue is in the precision of the type itself. It can be fixed by implementing a class for $$$\frac{p}{q}+\frac{r}{s}\sqrt{t}$$$, so I will consult the coordinator about replacing the model solution with one that uses exact computations. The current version of data was cross-validated with BurnedChicken's binary search solution, which made me believe it is precise enough.
Is Div2B is possible by doing just simple dfs?
No, it's too slow.
How?Shouldn't it be 4*10^5?Or I am making miscalculation here,can you give me the tc for a bfs for the test cases?
On each position in first string you will have 2 ways you can go, right and down, when you go right you do the same choice, but when you go down you have to go right to the end of the string, so in total you have O(n*(n+1)/2) time complexity, and because you have 10000 tests in one testcase you have n*(n+1)/2*10000 = 200'001'000'000'000 total operations which is obviously too much.
Can you please share the approach , thanks !
Interesting round! Really like it when there is an interactive problem in the round
Div. 2 PROBLEM B (Binary Path) video Editorial : YOUTUBE EDITORIAL LINK Audio : Hindi
Fast editorial, and...
using namespace atcoder;is found in problem 1E !This Round was really amazing. I really enjoyed this round
Why is the system testing frozen?
I am not sure but I think because the problem D1B — Pinball is conflicting
Issue from the server side.
https://codeforces.me/contest/1937/submission/248965536
Why is this giving tle? It is nlogn
You're keeping
nstrings in map, all of which have length more thann, soO(n^2)memory and even bigger time complexity.The first thing I can observe in your solution is that you should use
unordered_mapwhen the type of keys isstring. It uses hashed keys so that the problem due to the comparison time ofstringvalues can be resolved.Edit: Similarly, you can use
unordered_setinstead ofsetAlso you are deleting first charachter of a string and you are doing that n times so only that is O(n^2) which is too slow.
But isnt deleting the character an O(1) operation?
Nope, deleting character from a string is O(n)
deleting the last $$$m$$$ characters is $$$O(m)$$$, but deleting the first letters is like moving the rest to the front, which is $$$O(n)$$$.
Appending is the same way.
I love D1A = D2C. Very Beautiful problem!
Why do we try step 3 in Div2 C? Do we need to find the smallest one?
When you ask a question it uses bitwize or, but for answer you need bitwize xor
Yes.
A xor B = (A or B) - (A and B), and the candidates obtained after completing the step 2 satisfy the condition that the bit in a particular digit has a value of 1. It is because maximal value ofpi or pjis111...111(2)form.Yeah, I see. But I think when I finished the step 1, I can get the position of n-1. And then I don't understand why step 2 is needed. Assum that the position of n-1 is x. I think we can get the position of candidate that can make px^pk maximum without step 2. What is the mistake? This is my code but I got wrong answer. https://codeforces.me/contest/1937/submission/248971409 Please let me know the reason.
Super fast editorial
This is hard!
In Div 2 B, how to prove that if a=b, then it's optimal to move to the right?
If you go right, you always have the chance to go down.There by you can have minimum among those both
Thank you! I thought it won't always be optimal and therefore tried to solve it by dp
why is ffush giving idleness, but changing all to cout.flush() is AC
Because you have "ios_base::sync_with_stdio(false);" in your code so fflush doesn't affect cout.
Thank you for replying, I didnt know that.
for problem D2B — Binary Path ...
you can also use dp for counting number of paths. Submission
3d dp is too much to understand. I better stay away from it.
also possible with 2d dp
code
The first dimension is just the combination of two arrays
the array for visited checking
dp[0]and the array for the answer itselfdp[1]This doesn't increase the time complexity of the code; in fact, it optimizes the time complexity by avoiding the need to reassign the entire
dparray as not visited for each test case. Instead, I only need to check whether theidof the current state is equal to the current test'sid. If it is, then the current state has already been visited during the current test case.This is why there's a difference between our time complexities of our codes
I use
arrayinstead ofvectorand I don't reassign it at each test caseCan anybody explain this bigotry.
248984409 Global Dp arrays passes easily.
248971939 Dp arrays passed by reference gives MLE.
Is pass by reference soooo bad ?????
Exactly the same solution. The little rating points that I had are now gone. :(
In your submission with the DP-array passed as reference you accidentally create an n*n array instead of 2*n. :/
I'll go slap myself a couple hundred times. Thanks a lot for answering.
F: "Using nested ternary searches does not help very much. The time complexity will be $$$O(n \cdot log^{2}(1/ϵ))$$$, but the constants are large due to multiple function calls and floating point operations" lol 3 out of 4 accepted submissions use nested ternary searches
We tested nested ternary searches, but not golden section search. That was why I didn't see that coming. This is entirely my fault for not having considered.
Problem B can also be solved by dp. My submission https://codeforces.me/contest/1937/submission/24898172.First we create most optimal string and then apply dp for how many ways we can create this string.(Basically number of paths).
I used a similar approach to solve problem D2B: I'll explain it here to hopefully help someone. There are only n possibile way we can go from
(1,1)to(2,n), that are characterized by the point in which it goes downward. We want to remember this point.(1,n), otherwise we continue on the right.(1,i) == (2,i-1), for each decrementingi. This means that turning down before we did wouldn't have modified the path.Time complexity: O(n).
My submission as reference: 248990348.
Please can somebody tell me why this is giving TLE?
There is a square-root decomposition solve for bitwise paradox in $$$O(n\sqrt{n} + qlogn\sqrt{n})$$$, assuming DSU is $$$O(1)$$$. By breaking the array down into sqrt blocks, we can merge in ascending values of $$$a_i$$$ in each block and store the maximum prefix, suffix, and subarray OR in each block for such $$$a_i$$$. We can now simply binary search for a value $$$x$$$, merging blocks from left to right, keeping track of the current longest suffix and checking if the maximum subarray OR $$$\geq v$$$. Submission: 248991851
I tried same solution for Div1D, but I got some memory trouble and failed to solve within the contest time..... (I used 4 * 4 * N * sqrt(N) 8bit integers, which seems too large) My submission: 248971206
I made the blocks a bit bigger so my solution would take less memory, but my solution is still very tight on memory.
Same thing can be done using segment tree to reduce the memory to NlogN and complexity to NlogN 251321474
Can B be done with string hashing? After getting the best possible string, we can just try all possible paths in O(1) each?
Spoiler, it does work:
(used kactl hashing) 249355708
Thanks for the organizers, hated this contest
At div1 C, can't you just have edge from X[rank[i]] to i with cost 0, meaning that you defeat the pokemon i?
The solution to problem 1D is really similar to problem 1004F.
I modified about 3 lines of code and added a ST table and got accepted :(
For problem D1A — Bitwise Operation Wizard, we can actually reduce the number of queries needed to at most $$$2n$$$. Here's how.
From the editorial, we can see that we have $$$3$$$ steps, where the first step is finding first number (the editorial encourages us to find the maximum for this one) with $$$n-1$$$ queries, the second step is finding candidates for second number by finding maximum OR value with $$$n-2$$$ queries, and the third step is finding minimum from the candidates (since the minimum produces maximum XOR with the first number, the proof is left to the reader as exercise) with $$$sz-1$$$ queries, where $$$sz$$$ is the number of candidates and $$$sz \leq n$$$. This optimization mainly focuses on the first step.
Now, let $$$2^k < n \leq 2^{k+1}$$$ for some integer $$$k \geq 1$$$ (since $$$n = 2$$$ is pretty trivial lol). If we do our observation correctly, we'll notice that $$$p_i \oplus p_j \leq 2^{k+1}-1$$$. Funnily enough, we can reduce the number of queries in the first phase to $$$2^{k+1}-n$$$ queries. This can be done by realizing that any number from $$$2^{k+1}-n$$$ to $$$n-1$$$ are always valid candidates for the first number $$$p_i$$$, since they always have a second number $$$p_j \leq n-1$$$ such that $$$p_i \oplus p_j = 2^{k+1}-1$$$. And so, we only need to use $$$2^{k+1}-n$$$ queries to find any number that is $$$\geq 2^{k+1}-n$$$ (by knowing that the number is larger than at least $$$2^{k+1}-n$$$ other numbers).
From my calculation, from all of the possible permutations of $$$[0 \dots n-1]$$$, the third phase actually uses at most $$$n-2$$$ queries if $$$n = 2^{k+1}$$$ and at most $$$n - 2^k - 1$$$ queries otherwise, since the number of queries actually depends on the size of the candidates.
I believe the worst case can only happened at $$$n = 2^k+1$$$ and $$$n = 2^{k+1}$$$, where both only spent $$$2n-4$$$ queries. And thus, this problem is solved using $$$\leq 2n$$$ queries.
Edit: I found this during the round testing and suggested to add it as a hard version of the problem, but they refused lmao.
Edit 2: If anything seems wrong in this message, please let me know :3
Edit 3: Credit to MCYang for the concise upper bound for the step $$$3$$$ and some corrections to the comment ^w^
the submission
Interesting idea overall, though I think one of the steps needs some clarification.
In the explanation of step 3, when you mentioned that "$$$m$$$ is the number of active bits in the number $$$a$$$," $$$a$$$ actually comes out of nowhere. Does it mean a number we found at step 1? If so, why do you restrict the range of $$$a$$$ to $$$2^k\leq a<n$$$ (instead of $$$2^{k+1}-n\leq a<n$$$?) If not, what does $$$a$$$ refer to? You may want to describe what $$$a$$$ means more clearly.
By the way, I have a more concise expression for the upper bound on number of queries on step 3.
This also explains why the worst case of your idea happens only when $$$n=2^k+1$$$ or $$$n=2^{k+1}$$$. (Also they both only spend $$$2n-4$$$ queries. This is a resubmission of your code except that I added runtime checks on the number of queries.)
thanks man, will fix it :3
https://codeforces.me/contest/1937/submission/249016789 Why is this giving tle at 10th test case?
you did string assigning
ans = temp$$$n$$$ times, which results in $$$O(n^2)$$$ complexity since string assigning is $$$O(n)$$$.Thanks! Is there any way i can optimise that approach?
hint: notice that everytime, you only need to change one character inside the temp string, which means that when you need to change ans, you can do so by only changing one character inside of it
:_), yea that makes sense. Thanks edit- still tle.
else if(temp==ans) x++;is $$$O(n)$$$ sincetempandansare strings of length $$$O(n)$$$. This makes your code $$$O(n^2)$$$.Fixed that, got AC. Thanks!
can anyone help me in this DIV2 -B
int n;
void solve(){
cin>>n; string u, d; cin>>u>>d; string s = u[0] + d; string c=s; int cnt=0; for(int i=0;i<n;i++){ s[i] = u[i]; s[i+1] = d[i]; if(s==c) cnt++; if(s<c) c=s, cnt=1; } cout<<c<<'\n'<<cnt<<'\n';}
It is giving TLE -- but it is running in O(n) time
May be the way you are checking s<c is taking O(n) time itself for each iteration
I uploaded to Youtube a video in English explaining the solution of Div2-B
248985883
Can you help me? I am getting TLE. But my code is supposed to be in NlogN time only.
can anyone prove/justify Step 3 of editorial of D2C/D1A.why minimum need to be choosen.
Cause the minimum is the one that does not have any bit in common with n-1, therefore maximazing the XOR.
I will share my solution for D1F.
First, binary search for $$$r$$$. The maximum circle has radius at least $$$r$$$ is equivalent to the $$$n$$$ circles with their radius decreased by $$$r$$$ have a non-empty intersection. If the intersection is non-empty, the intersection is convex.
Then do binary search for $$$y$$$. For $$$y=k$$$, one of the following is true:
The first case is true if and only if
Otherwise, there exists two circles $$$i,j$$$ such that $$$r_i<l_j$$$. The second case is true if and only if the intersection of the circles $$$i,j$$$ is entirely in the $$$y>k$$$ half-plane. There are many ways to check this.
Problem D can be done in $$$O(\log V\log\log V)$$$ per query of type 1 and $$$O(\log n)$$$ per query of type 2. The idea is to maintain all minimal good intervals $$$[l,r]$$$ (good intervals such that neither $$$[l+1,r]$$$ and $$$[l,r-1]$$$ are good) in sorted order using a BBST.
My Screencast for A and B problems: https://youtube.com/live/IU6Zqy5LGB4 This was private during the contest. Hope it helps someone.
Bro no one is interested in seeing you struggling in problem A, so stop spamming the commemt section under every blog post
I apologize, bro. I understand that my struggle with problem A, taking 3 minutes to solve (which may seem slow to you for someone "green"), might not be of interest to everyone. I acknowledge that I need to improve, and I'll work harder in the future.
Regarding your statement that 'no one wants to watch,' I must respectfully disagree. I get over 30 (sometimes 100) watch hours on these videos in total, indicating that there is indeed interest. However, if my content doesn't resonate with you, you're welcome to unsubscribe and find content that better suits your preferences. Criticizing someone's honest efforts without constructive feedback isn't fair or productive.
why are you specifically mentinoning "green". making fun of someone's rating without constructive feedback isn't fair or productive.
I was talking about me... i am green so it will take time to solve.
oh, I thought you were teasing me. Sorry
Round 930 div 2 problem C: code -> 249045846
Idleness limit exceeded on test 1 why? what's wrong? Please identify the mistake and let me know
If you read interactive problems guidelines, you shouldn't do this
#define endl "\n"sir why? using normal endl doesnt flushes? i have to use cout.flush() externally. is it because of ios sync? part?
Problem D1B Pinball can be done in
O(n)time: No need to binary search for the proper endings, as they are changing monotonically as you go from one query index i to i+1. 249059259In the editorial for D2B , I think the initial value of 'max_down' should be (n-1). correct me if I am wrong
The influence of clash of D1B is quite big. it appears just following the beginning problem and people soon finds the clash, as you can see a originally *2400 problem(733E) passed by a lot of people. my advise is just make this round unrated if possible.
Good idea hh
I am not able to understand problem D ??? Div2
In F I solved the 3-circle case like this: I applied an inversion at one of the intersection points of 2 circles and found a circle inscribed between an arc and 2 segments with Sawayama theorem. Unfortunately after inversion the picture becomes heavily dependant on the point configuration, and I think my code that passed doesn't quite work (though I don't understand how), as it sometimes finds no circles between the given 3 at all
Edit: Also now it works insanely fast without hypotl calls
How to get pupil rank?
For the problem D, at the end of the editorial, they said : It is not difficult to observe that we can use prefix sum to store the sum of indices, and then quickly calculate the time when the pinball moves.
And to calculate the pinball moves the precalculate two arrays: IDr[i]=IDr[i-1]+i*(s[i-1]=='>'); IDl[i]=IDl[i-1]+i*(s[i-1]=='<');
and for case s[i-1] == '<' && countright(1,p) > countleft(p+1,n), the ball should go at the end, from leftk to boundary. But the moves was got in such a way:
2*((IDl[n]-IDl[i])-(IDr[i]-IDr[k-1]))+i+(n+1) with k the last movemement before go out.
In D1C,why add Y node? edge x -> Pokémon node with a value of 0?
Can someone please help me in finding the mistake in the following code? Here , I have first calculated the index , which means that the substring b starting from index to n-1 is lexicographically smaller or equal to the substring a from index+1 to n.
Submission
Can someone pls review my code and tell me in which test code my code is getting error :) https://codeforces.me/contest/1937/submission/249344544
Can someone please explain how do we derive the formula for Problem D? I'm so confused!
Problem c sucks!!
What is line segment tree mentioned in div 1 D?
Did the tutorial of Div.1 E missed some factorial notations in the final transform formulas of $$$f$$$?
For example $$$f_i = -\sum_{j=0}^{last_i} f_j \cdot A_{i-j-1}^{P_i-j-1} = -(P_i-i)^{-1} \sum_{j=0}^{last_i} f_j \cdot (P_i-j-1)$$$, I think it should be $$$f_i = -\sum_{j=0}^{last_i} f_j \cdot A_{i-j-1}^{P_i-j-1} = -((P_i-i) {\color{red}!} )^{-1} \sum_{j=0}^{last_i} f_j \cdot (P_i-j-1) {\color{red}!}$$$.
And if this is correct, how can we do D&C + FFT with $$$(P_i-j-1)!$$$ in the formula?
Thx,typo fixed.
You can read https://mirror.codeforces.com/blog/entry/18842 for D&C + FFT tricks(in DIV1E).
I had the same question as you, because the editorial made me think that the formula $$$f(i) = h(i)\sum f(j)g(p_i-j)$$$ can be written in the form $$$f(i) = h(i)\sum f(j)g(i-j)$$$ somehow. This is not true. Instead, when performing the convolution step, you compute $$$F(i) = \sum f(j)g(i-j)$$$ and then take $$$f(i) = h(i)F(p_i)$$$. Note that unlike the example 553E - Kyoya and Train that wuhudsm referenced, in the convolution step you may be performing a convolution of vectors of very different sizes. Due to $$$p$$$ being an increasing function from $$$0$$$ to $$$n$$$, the time complexity works out correctly in the end (in my opinion, the editorial would be improved if it explained this part).
Thanks wuhudsm for the great tutorial for problem div2 E (Pokemon Arena).
However, I think there's a typo in the first line of the tutorial. It makes more sense to be like that, Then the problem is essentially finding the shortest path from $$$1$$$ to $$$n$$$ and not from $$$n$$$ to $$$1$$$ as written in the tutorial.
Please correct me if I am wrong.
D1E, am I right that last_i = max(j<i)(P_j!=P_i)? Or j can be greater than i?
Div1D can support range update and only use one segment tree if we design our node to have logV merge. See 251321474 See node in struct MinGood, it will have a bit more memory O(NlogN) (logN per node) but that still fits.
Solution to Div 2 problem E reminds me of the graph construction we do for proving NP-Completeness of certain problems. Can someone suggest problems to get good at thinking like this?
Another solution for Div1C with segment tree.
Let's say we want to process a pokemon $$$i$$$. Where could the path possibly come from? Let's assume the path comes from trait $$$j$$$, then either the path comes from a pokemon with more strength (1) or a pokemon with less or same strength (2).
If it comes from a pokemon with more strength (1) (let's say pokemon $$$p$$$), then $$$dist_i = dist_p + a_{p,j} - a_{i,j} + c_i$$$.
If it comes from a pokemon with less or same strength (2), then $$$dist_i = dist_p + c_i$$$, since we don't have to raise the stats of pokemon $$$i$$$.
But, what if the shortest path to $$$p$$$ also used trait $$$j$$$? Let's call $$$q$$$ the parent of $$$p$$$. Then our path looks like $$$q$$$ -> $$$p$$$ -> $$$i$$$. However, we could take the path $$$q$$$ -> $$$i$$$ and get a lower cost. So this case never happens. More generally, we will never use the same trait twice in a row.
But how do we consider all possible $$$p$$$ at once? To cover case 1, we want the lowest value of $$$dist_p + a_{p,j}$$$ across all $$$p$$$ where $$$a_{p,j} > a_{i,j}$$$. If we sort $$$a$$$ so that all $$$p$$$ form a contiguous segment, this turns into a range min query. To cover case 2, we take the lowest value of $$$dist_p$$$ across all $$$p$$$ where $$$a_{p,j} \le a_{i,j}$$$, also a range min query.
So we can store two segment trees for each $$$j$$$, each with size $$$O(n)$$$, to quickly determine the shortest path assuming all nodes with lower cost are already processed. All that is left is to determine processing order, and that can be done with priority queue/Dijkstra. The time complexity is $$$O(nm \log(nm))$$$.
did you write div1e tutorial code so that it couldn't be read by normal people