Code Jam R2 starts today at 14:00 UTC. Don't miss!
Top 1000 contestants will receive t-shirts.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Code Jam R2 starts today at 14:00 UTC. Don't miss!
Top 1000 contestants will receive t-shirts.
| Название |
|---|



1
The top 500 contestants will advance to Round 3 to compete for finalist spots and a free trip to Google Los Angeles. :)
Как решать задачу B?
I used a greedy algorithm that moves the numbers in increasing order one after another to the correct places. You can always move the number either to the left or to the right and select the direction that minimizes the number of swaps.
For example, if the array is [6, 4, 1, 5, 2, 3], we first move number 1. If we move it to the left, we need 2 swaps, and if we move it to the right, we need 3 swaps. So we move it to the left and the array becomes [1, 6, 4, 5, 2, 3]. After this, we move number 2 etc.
У меня такое решение задачи В: сначала двигаем 1 к ближайшему краю, потом решаем меньшую задачу. Вопрос: как доказать, что оно правильное?
Можно чуть поподробнее: вот мы сдвинули min элемент в самое лево. И что дальше?
То же самое для оставшихся элементов.
3 1 2 5 6 7
Сдвинули 1 влево и решаем для 3 2 5 6 7
Наименьшее число должно стоять в одном из краев, причем должно быть поменяно со всеми элементами левее/правее него. На обмены других элементов это не влияет.
Спасибо <3
Ключевое наблюдение — если мы выставили n+m минимальных элементов в префикс и суффикс, то позиция минимального из еще не выставленных элементов относительно других еще не выставленных элементов не зависит от значений n и m (только от начальной перестановки и значения n+m). Поэтому выбор более близкого края не влияет ни на что в дальнейшем.
Вне зависимости от остальных сдвигов 1 будет на одном из краёв. Чтобы передвинуть её на левый край, её в любом случае придётся обменять со всеми теми, которые больше неё и левее (опять, вне зависимости от всех остальных сдвигов и их порядка: если есть кто-то больше и левее, с ним необходимо будет рано или поздно поменяться), т.е. просто больше, т.к. мы двигаем именно 1. Итак, за меньшее число обменов не получится, а ровно за такое это делается тривиально.
C — дичайший баян. Искренне удивлен присутствию такой задачи на контесте.
Для тех, кто не знает, как это решать — прочитайте разбор на medium с TCO 2013 3A.
Я решал эту задачу на опенкапе лет пять назад.
Я ее видел на одном из Всесибов.
Я ее решал на одном из опенкапов. Так было что-то про тараканов, которые очередями пересекают кухню.
Первые 3 — бояны. Вероятно, я бы мог такое сказать и о четвертой, если бы на контестах читал все задачи))
Первая была где-то на кодчефе, была на снарке в прошлом году, да и вообще боян.
Вторая была на каком-то из regionals.
Третья была на ТСO, на Opencup и на Challenge 24.
А вот я не искал легких путей и написал ее обходом лабиринта по правилу правой руки...
Вы не одиноки, Jokser писал то же самое :).
Наверно надо избавиться от int gr[w][h], и хранить путь как массив вертикальных отрезков или что-то типа такого =)
Напомню, что можно поставить галочку в Solution Download в таблице результатов, и после этого загрузить исходник любого участника по любой задаче.
Ага... Как минимум я её давал на очный тур всесиба несколько лет назад. Только там все координаты были до 10^9, чтобы не было соблазна что-то изобрести =)
Ну и до кучи, в евклидой метрике и чуть-чуть другой формулировке она была на школьних летних сборах России 2010 года.
Разбор задач
Задача A. Будем использовать жадный алгоритм. Детали предоставляются на усмотрение читателю.
Задача B. Будем обрабатывать элементы в порядке убывания значения. Добавляя очередной элемент, будем решать, ставить его до всех уже обработанных элементов или после. При этом будем учитывать только перестановки с уже обработанными элементами. Доказательство корректности предоставляется читателю.
Задача C. Заметим, что можно искать не максимальный поток, а минимальный разрез. Разрез — это путь, который начинается от одного берега, возможно, проходит по некоторым зданиям и достигает другого берега. При этом расстояние между двумя зданиями — это максимум из расстояний между их проекциями на ось X и на ось Y.
Задача D. Заметим, что каждая из вершин каждого из новых trie соответствует какой-то вершине исходного trie. Для каждой из вершин исходного trie определим, на сколько серверов она может попасть. Пусть через i-ю вершину проходит Ci строк. Тогда число таких серверов не может быть больше Ci. Кроме того, оно, очевидно, не больше N. Заметим, что оно может быть равно min(Ci, N): если Ci < N, то распределим все строки по разным серверам, иначе распределим их так, чтобы на каждый сервер попала хотя бы одна строка. Заметим, что эти условия можно выполнить для всех вершин одновременно. Соответственно, чтобы посчитать X, просуммируем min(Ci, N) по всем вершинам. Чтобы посчитать Y, разделим вершины на те, для которых Ci ≥ N, и все остальные. Если у хотя бы одного потомка некоторой вершины Ci ≥ N, то условие для самой вершины автоматически выполняется, если оно выполняется для потомка, значит, количество комбинаций получается перемножением количества комбинаций для потомков. Если Ci < N, то количество комбинаций равно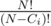 . Остаётся случай, когда у вершины, но ни у одного из её потомков, Ci ≥ N. В этом случае также перемножим ответы для потомков, но теперь в ответ попадут комбинации, где на некоторые серверы не попало ни одной строки. Чтобы учесть такие случаи, можно воспользоваться формулой включения-исключения. Детали предоставляются на усмотрение читателю.
. Остаётся случай, когда у вершины, но ни у одного из её потомков, Ci ≥ N. В этом случае также перемножим ответы для потомков, но теперь в ответ попадут комбинации, где на некоторые серверы не попало ни одной строки. Чтобы учесть такие случаи, можно воспользоваться формулой включения-исключения. Детали предоставляются на усмотрение читателю.
Решил D примерно как ты сказал, но неправильно. В результате написал там ещё и динамику по поддеревьям, она-то и прошла :)
Fellow coders,
Can someone explain why this solution for A fails to terminate for small testcase in Xcode IDE? Can you find any other IDE where it behaves the same way?
I pulled a rng_58 :D
I submitted A's output file for B and was debugging for 45 minutes. It doesn't matter because I am still getting a tshirt, which was my target :P
Actually, you pulled a jodik. In March 2012 on Slovak OI nationals (practical day: 2 problems, 15 points each, IOI scoring, full feedback, last submission counts), he resubmitted one problem's solution on another problem (for which he had full score), and then again on the correct one, where he found out that it's still a wrong solution, giving him 0 points total :D
Fortunately, he managed to convince the organizers to accept his earlier solution, so he did get the points in the end.
What do you mean by 'full feedback'? Didn't he have the time to resubmit or what?
In Russia we have the rule that your submission for a problem should pass example test cases (ones from the statement) to be accepted for a full testing, no matter what. It's very useful to avoid such mistakes and double-check I/O issues.
This happened about 5 minutes before the end of the contest... and the testing takes a while. Because full feedback. And because Jodik, of course — after seeing that he's suddenly got 0 points, he panicks and starts trying to find out what happened, starting from the least probably causes.
I've had 1 or 2 submissions that passed all but 1 sample, so it can be a bit tricky. Besides, it can be annoying in case of partial scoring (hardwiring an output for a particular input).
Ages ago, when USACO didn't had online submission server and all the submissions were done via e-mail, one participant's code was mixed up and submitted for another problem.
The unique element of this story is that it still scored 40% of points.
Can anyone explain how D-large is solved? Tks~
Dynamic programming in subtrees — for every node of trie, for every 0 ≤ n ≤ N calculate maximum number of nodes if subtree is stored on n servers.
Actually, for each node of the trie, count the number e of strings ending in its subtree; the answer (first part) is then the sum of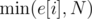 over all nodes. It obviously works, since you can just split the strings ending in each subtree into as many servers as possible.
over all nodes. It obviously works, since you can just split the strings ending in each subtree into as many servers as possible.
Можно подробнее про переходы в динамике? Как считать dp[i][j] = ???
My solution:
construct the original trie; for each vertex, remember how many strings ended exactly in it (
e[v]) and how many ended in its subtree (s[v]); it's clear that we can putmin(s[v],N)strings (as many as possible) from its subtree into distinct servers, so each vertex appears this many times and the first part of the answer is the sum ofmin(s[v],N)over all vertices (including the one corresponding to the empty prefix)it's also clear that we can only achieve this many vertices in total if these bounds are exactly satisfied for each vertex, so:
in the second case, if the strings in some son's subtree span over all servers, then the ones in the parent's subtree also do; also, if the strings in a parent's subtree are all in distinct servers, then the strings in any son's subtree also are, so the conditions for the remaining vertices are automatically satisfied; this set of conditions is also necessary
feel free to pre-calculate all factorials, their modular inverses and binomial coefficients up to 5000x5000
there are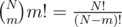 ways to put m < N strings into m servers out of N — we choose the servers with one string and then the order of placing the strings; in the second type of vertices, m = s[v]
ways to put m < N strings into m servers out of N — we choose the servers with one string and then the order of placing the strings; in the second type of vertices, m = s[v]
let P(m, n) be the number of ways of putting m strings (from a specific subtree) into n servers (m ≥ N ≥ n) in such a way that there's at least 1 string in each server (the strings span over all n servers), and P0(m, n) the number of ways when we allow some server to not contain any of these strings; then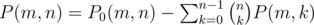 , because we just subtract the choices that end up with exactly n - k > 0 servers empty
, because we just subtract the choices that end up with exactly n - k > 0 servers empty
we can calculate P0 by realizing that each of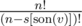 over all sons of v
over all sons of v
e[v]strings can go into any server and each son of v (the subtree's root) must satisfy the condition above, and these rules are independent, so P0 is the product of e[v]n andusing modular exponentiation, we can calculate P0(m, n) for any subtree in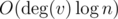 time; then, we can DP all P(m, n) up to P(m, N) (which is the actual number of ways that satisfy the basic condition for v) in
time; then, we can DP all P(m, n) up to P(m, N) (which is the actual number of ways that satisfy the basic condition for v) in 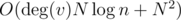 time; over all vertices, we get worst-case
time; over all vertices, we get worst-case 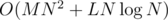 , where L is the total length of strings in the input
, where L is the total length of strings in the input
the second part of the answer is just the product of ways to satify the conditions for all vertices, for which they need to be satisfied (P(m, N) or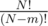 )
)
C was a very interesting problem in my opinion. I created a graph where building and left and right (not up and down) banks were vertices and cost of edge was maximum od distance between those two things on x and on y axis (minimum number of diagonally touching cells we have to mark to connect those two vertices) and found a shortest way from left to the right bank. Complexity O(b^2 log b) (Dijkstra). This is computing a mincut which is in fact also a maxflow. h and w don't matter for me.
I agree. C was a beautiful problem. Mincut -> Maxflow is a common theme in programming contests, but it's so rare to see it go the other way around.
There was a discussion in Russian about this problem.
I told that this problem definitely isn't a "brand new problem", because it's idea is pretty similar to one for problem 600 from TCO 2013 3A.
Others have found other contests where exactly this problem was given.
But I still agree that this problem is beautyful (the problem from TCO is even more beautiful IMHO).
Does Google also ship the T-Shirts outside of the US? When will they ship them?
Last year, I got mine at the end of August. If you hope to get it soon, you'll probably be disappointed...
In my case, it was shipped around 6 to 7 months later.