Всем привет! Недавно меня заинтересовала такая задача: дано дерево с корнем в вершине 0. Поступают запросы двух видов.
- Добавить к вершине k сына.
- Выдать номер предка вершины k, у которого высота равна h.
Вершины пронумерованы в порядке добавления.
Пока что я знаю только два метода решения:
- Двоичный подъём. Ну тут всё очевидно,
времени и памяти. - С помощью индексированного двоичного дерева поиска (например, неявная дерамида) поддерживаем эйлеров обход графа. Далее либо сводим к k-ой порядковой статистике на префиксе, либо храним для каждой высоты список вершин и находим нужную бинарным поиском. Это потребует O(n) памяти, но времени
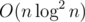(возможно, при грамотной реализации можно и , но я точно не знаю), ещё и с большущей константой.
Интересно то, что оба метода подозрительно похожи на LCA. В связи с этим возникает вопрос — может, задачу можно как-то свести к LCA непосредственно? Ну и, конечно, интересно, какие ещё есть способы решения этой задачи, в том числе и в оффлайне.
В этой статье очень внятно изложено, что вообще по этой теме известно, в частности, если нет запросов изменения, алгоритм за O(N) - O(1).
BTW, в оффлайне решение очень простое. Во время обхода в глубину можно хранить стек предков и получать ответы на запросы за O(1).