Thank you for participation and we hope you enjoy this round ヽ(^ o ^)/.
During the contest, there was a small issue in problem D. For those affected, we have skipped your duplicate submissions (if your duplicate submissions were not skipped, please let us know). We apologize again for any inconvenience caused.
In addition, we are honored to invite you to our unofficial round tomorrow (*╹▽╹*) Invitation to TheForces Round #22 (Interesting-Forces)
1864A-Increasing and Decreasing
Idea : wuhudsm
We use the following greedy construction:
For all $$$i$$$ ($$$1<i<n$$$), set $$$a_i=a_{i+1}-(n-i)$$$. If $$$a_2-a_1 \geq n-1$$$, we've found a solution, otherwise there is no solution.
Proof. Assume there's a solution which includes an index $$$i$$$ ($$$1<i<n$$$) such that $$$a_{i+1}-a_i>n-i$$$. We can make $$$a_j:=a_j+\Delta$$$ for all $$$j$$$ ($$$2 \le j \le i$$$), where $$$\Delta=a_{i+1}-a_i-(n-i)$$$. After several processes like this, we get a solution the same as greedy construction gives. This leads to a contradiction.
#include <bits/stdc++.h>
#define all(a) (a).begin(), (a).end()
#define sz(a) (int)(a).size()
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int tt;
cin >> tt;
while (tt--) {
int x, y, n;
cin >> x >> y >> n;
vector<int> a(n);
a[0] = x, a[n - 1] = y;
int d = 1;
for (int i = n - 2; i >= 1; --i) {
a[i] = a[i + 1] - d;
++d;
}
bool ok = true;
for (int i = 0; i + 1 < n; ++i) {
if (a[i + 1] <= a[i]) {
ok = false;
}
}
for (int i = 0; i + 2 < n; ++i) {
int p = a[i + 1] - a[i];
int q = a[i + 2] - a[i + 1];
if (p <= q) {
ok = false;
}
}
if (!ok) {
cout << "-1\n";
continue;
}
for (int i = 0; i < n; ++i) {
cout << a[i] << " ";
}
cout << "\n";
}
}
1864B-Swap and Reverse
Idea : Amir_Parsa, chromate00
By the first kind of operation, we already know that every odd index (same for the even ones) can be swapped with each other freely. Therefore, let us write down the values of the indices modulo $$$2$$$. For example, if $$$n$$$ is $$$10$$$, the indices modulo $$$2$$$ are $$$[1,0,1,0,1,0,1,0,1,0]$$$. Now, we consider the two cases.
- When $$$k$$$ is odd.
We can find out that after reversing any subarray of length $$$k$$$, the indices modulo $$$2$$$ do not change. So in this case, any series of the second operation is identical to some series of the first operation. Therefore, you should sort the odd indices and the even indices separately, and output the result of merging them into one string.
- When $$$k$$$ is even.
Let us observe how we can swap two adjacent indices in this case. First, reverse $$$[i,i+k-1]$$$, and then reverse $$$[i+1,i+k]$$$. If we do this on $$$[1,0,1,0,1,0,1,0,1,0]$$$, assuming $$$i=1$$$ and $$$k=6$$$, the indices modulo $$$2$$$ turn into $$$[0,1,0,1,0,1,1,0,1,0]$$$, and then $$$[0,1,1,0,1,0,1,0,1,0]$$$. Using these two steps and some series of the first operation, we can see that we can swap any two adjacent indices as a result. And such a series of operation is always possible, as $$$k<n$$$. Therefore, we can sort the entire string, and output the result.
#include <bits/stdc++.h>
#define all(a) (a).begin(), (a).end()
#define sz(a) (int)(a).size()
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int tt;
cin >> tt;
while (tt--) {
int n, k;
cin >> n >> k;
string s;
cin >> s;
vector<char> odd, even;
for (int i = 0; i < n; ++i) {
if (i % 2 == 0) {
even.pb(s[i]);
} else {
odd.pb(s[i]);
}
}
sort(all(even));
sort(all(odd));
string ans1 = "";
for (int i = 0, j = 0; i < sz(even) || j < sz(odd); ++i, ++j) {
if (i < sz(even)) {
ans1 += even[i];
}
if (j < sz(odd)) {
ans1 += odd[i];
}
}
if (k % 2 == 0) {
sort(all(s));
cout << s << "\n";
continue;
}
cout << ans1 << "\n";
}
}
Try to solve the problem if $$$n = k$$$ was allowed.
1864C-Divisor Chain
Idea : wuhudsm
Let us divide the task into two steps, on each step we will use each divisor at most once. For convenience, let us denote $$$L$$$ as the largest value, such that $$$2^L \le x$$$ holds. The two steps are as follows.
- Reduce $$$x$$$ to $$$2^L$$$.
Given any integer $$$x$$$, we can see that its lowest significant bit is a divisor of $$$x$$$. If $$$x$$$ has more than one bit, we can repeatedly subtract the value corresponding to the lowest significant bit of $$$x$$$. When $$$x$$$ finally has only one bit, finish the first step. In this step, we have only used each significant bit of $$$x$$$ at most once.
- Reduce $$$2^L$$$ to $$$1$$$.
We can find a way to reduce $$$2^L$$$ to $$$1$$$ by using each bit exactly once. Formally, if $$$k \ge 0$$$, then $$$2^{k+1}-2^k=2^k$$$, and $$$2^k$$$ is a divisor of $$$2^{k+1}$$$. Thus, by subtracting $$$2^{L-1},2^{L-2},\ldots,1$$$ in order, we reach $$$1$$$ from $$$2^L$$$ by using each bit from the $$$0$$$-th bit to the $$$(L-1)$$$-st bit exactly once.
As a result, we can reduce $$$x$$$ to $$$1$$$ by using each power of $$$2$$$ at most twice (once from the first step, once from the second step). Since we used each bit at most twice, the time complexity for solving one test case is $$$O(\log x)$$$.
Due to the lenient constraints, some solutions with $$$O(\sqrt x)$$$ time complexity should pass as well (as long as they fit into the $$$1000$$$ operations limit).
#include <bits/stdc++.h>
#define all(a) (a).begin(), (a).end()
#define sz(a) (int)(a).size()
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
bool bit(int mask, int pos) {
return (mask >> pos) & 1;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int tt;
cin >> tt;
while (tt--) {
int x;
cin >> x;
int p;
vector<int> ans;
ans.pb(x);
for (int i = 0; ; ++i) {
if (bit(x, i)) {
if (x == (1 << i)) {
p = i;
break;
}
x -= (1 << i);
ans.pb(x);
}
}
while (p > 0) {
x -= (1 << (p - 1));
ans.pb(x);
--p;
}
cout << sz(ans) << "\n";
for (int y : ans) {
cout << y << " ";
}
cout << "\n";
}
}
1864D-Matrix Cascade
Idea : AquaMoon
Firstly, the first row has some elements that are $$$\text{1}$$$ s and some elements that are $$$\text{0}$$$ s. The elements that are $$$\text{1}$$$ can only be turned into $$$\text{0}$$$ by operating on the corresponding cell an odd number of times, and the elements that are $$$\text{0}$$$ can only be turned into $$$\text{0}$$$ by operating on the corresponding cell an even number of times. Two operations on the same cell are equivalent to no operation, so only one operation is performed on the corresponding cell of the element that is $$$\text{1}$$$ in the first row. Thus, the operation on the first row is deterministic. Subsequent rows are affected by the operations in the first row, so it is sufficient to proceed to consider rows $$$2$$$ to $$$n$$$ in the same way.
Now consider how to quickly deal with the effect of the preceding rows on the following rows. An operation on position $$$(x,y)$$$ will simultaneously invert all the elements from column $$$y-1$$$ to column $$$y+1$$$ in row $$$x+1$$$, and from column $$$y-2$$$ to column $$$y+2$$$ in row $$$x+2$$$, and son on. Thus, the elements being inverted are exactly the portion of the matrix sandwiched between lines passing through $$$(x,y)$$$ with slopes $$$1$$$ and $$$-1$$$. Let $$$b$$$ denote the effect of the line with slope $$$1$$$ from all predecing rows, and let $$$c$$$ denote the effect of the line with slope $$$-1$$$ from all preceding rows. % To optimize complexity, $$$b$$$, $$$c$$$ are both obtained using difference arrays to the current line using prefix sums to obtain the $$$b,c$$$ values at that time.
After an operation on $$$(i,j)$$$, $$$b[i+1][j-1]$$$ is marked, and $$$c[i+1][j+2]$$$ is marked. Next, $$$b[i][j]$$$ inherits $$$b[i-1][j+1]$$$, and $$$c[i][j]$$$ inherits $$$c[i-1][j-1]$$$. For the current row, the effect of the previous rows is obtained by maintaining the prefix sums on $$$b$$$ and $$$c$$$. The total complexity is $$$O(n^2)$$$.
#include <bits/stdc++.h>
#define all(a) (a).begin(), (a).end()
#define sz(a) (int)(a).size()
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int tt;
cin >> tt;
while (tt--) {
int n;
cin >> n;
vector<string> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
int ans = 0;
vector<vector<int> > val(n, vector<int>(n, 0));
vector<vector<int> > sum(n, vector<int>(n, 0));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0) {
} else if (i == 1) {
for (int k = max(0, j - 1); k <= min(j + 1, n - 1); ++k) {
sum[i][j] ^= sum[i - 1][k];
}
} else {
if (j == 0) {
sum[i][j] ^= sum[i - 2][j];
} else {
sum[i][j] ^= sum[i - 1][j - 1];
}
if (j == n - 1) {
sum[i][j] ^= sum[i - 2][j];
} else {
sum[i][j] ^= sum[i - 1][j + 1];
}
sum[i][j] ^= sum[i - 2][j];
sum[i][j] ^= val[i - 1][j];
}
if (sum[i][j] ^ (a[i][j] - '0')) {
++ans;
sum[i][j] ^= 1;
val[i][j] = 1;
}
}
}
cout << ans << "\n";
}
}
1864E-Guess Game
Idea : wuhudsm
First, let's analize a single game for fixed $$$a$$$, $$$b$$$, and how many turns it takes.
Consider the binary representation of $$$a \mid b$$$. We consider bits from highest to lowest. For bits with a value of $$$0$$$, we can ignore it because it firmly tells us that both bits of $$$a$$$ and $$$b$$$ are $$$0$$$. For convenience, we assume that all bits of $$$a \mid b$$$ are $$$1$$$.
In the first round, if the highest bit of $$$a$$$ is $$$0$$$, then Alice can immediately say that $$$a<b$$$. Otherwise, in the second round of the game, Bob knows that the highest bit of $$$a$$$ is not $$$0$$$. If the highest or the second highest bit of b is $$$0$$$, then Bob can immediately say that $$$a>b$$$. Otherwise, in the third round of the game, Alice knows that the highest and the second highest bits of $$$b$$$ are not $$$0$$$, and so on.
Consider only set bits in $$$a \mid b$$$. Let's enumerate these bits from highest to lowest. After some observation, we can conclude that:
- If $$$a<b$$$ and the $$$i$$$-th bit in $$$a$$$ is zero, then the answer is $$$i+1−(i\%2 == 1)$$$;
- If $$$a=b$$$, then the answer is $$$k+1$$$, where $$$k$$$ is the number of set bits in $$$a \mid b$$$;
- If $$$a>b$$$ and the $$$i$$$-th bit in $$$b$$$ is zero, then the answer is $$$i+(i\%2 == 1)$$$.
Now that we have a brute force algorithm for $$$O (n^2 \log A)$$$, how can we optimize it?
We can build a bit trie and traverse all nodes. We can easily calculate the number of $$$1$$$s that pass from a node to the root node, as well as the number of numbers prefixed with it and followed by $$$0$$$ (or $$$1$$$). Use this information to calculate the answer.
#include <bits/stdc++.h>
#define all(a) (a).begin(), (a).end()
#define sz(a) (int)(a).size()
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
struct node {
int to[2];
int cnt;
node() {
to[0] = to[1] = -1;
cnt = 0;
}
};
bool bit(int mask, int pos) {
return (mask >> pos) & 1;
}
vector<node> t;
void add(int x) {
int v = 0;
for (int i = 29; i >= 0; --i) {
int b = bit(x, i);
if (t[v].to[b] == -1) {
t[v].to[b] = sz(t);
t.pb(node());
}
++t[v].cnt;
v = t[v].to[b];
}
++t[v].cnt;
}
const int mod = 998244353;
void mul(int& a, int b) {
ll c = ll(a) * b;
if (c >= mod) {
c %= mod;
}
a = c;
}
int binpow(int a, int n) {
int ans = 1;
while (n) {
if (n & 1) {
mul(ans, a);
}
mul(a, a);
n >>= 1;
}
return ans;
}
void solve(int v, int k, ll& ans) {
if (t[v].to[0] != -1 && t[v].to[1] != -1) {
ll i = k + 1;
ans += (2 * (i / 2) + 1) * t[t[v].to[0]].cnt * t[t[v].to[1]].cnt;
ans += 2 * ((i + 1) / 2) * t[t[v].to[0]].cnt * t[t[v].to[1]].cnt;
}
if (t[v].to[0] == -1 && t[v].to[1] == -1) {
ll i = k + 1;
ans += i * t[v].cnt * t[v].cnt;
}
if (t[v].to[0] != -1) {
solve(t[v].to[0], k, ans);
}
if (t[v].to[1] != -1) {
solve(t[v].to[1], k + 1, ans);
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int tt;
cin >> tt;
while (tt--) {
t.clear();
t.pb(node());
int n;
cin >> n;
for (int i = 0; i < n; ++i) {
int a;
cin >> a;
add(a);
}
ll x = 0;
solve(0, 0, x);
int ans = x % mod;
mul(ans, binpow(n, mod - 2));
mul(ans, binpow(n, mod - 2));
cout << ans << "\n";
}
}
1864F-Exotic Queries
The final solution is irrelevant to Cartesian trees.
First, we consider only the sequence of elements to be manipulated. We claim that it is optimal to operate on the whole sequence so that the minimum elements are all decreased to $$$0$$$, and then solve the problem on the segments separated by the $0$s recursively.
A straightforward corollary of the claim is that two equal elements between which there are no smaller elements are handled in a single operation, so the final answer is $$$\ell$$$ (the number of elements to be manipulated) minus the number of such adjacent pairs.
Proof: Define $$$S(l, r)$$$ to be the answer for the segment $$$[l, r]$$$. Do induction on the length of the segment. If the first operation does not manipulate the whole segment, the segment will be separated into several independent parts by the first operation, for the non-inclusive operations cannot intersect, and the final answer, which is the sum of $$$S$$$ of the parts, will not be less than the initial answer according to the corollary, for some of the equal pairs are separated.
Now the original problem is converted into a data structure task. Consider all adjacent equal pairs $$$(l, r)$$$, and $$$m$$$ is the maximum element between $$$(l, r)$$$, $m < a_l$. $$$(l, r)$$$ decrease the answer if and only if $$$m < L \le a_l = a_r \le R$$$, which can be easily calculated with a segment tree and sweeping lines.
#include <bits/stdc++.h>
#define all(a) (a).begin(), (a).end()
#define sz(a) (int)(a).size()
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
vector<int> sum;
int N;
void updSumTree(int pos) {
for (pos += N; pos; pos >>= 1) {
++sum[pos];
}
}
int getSumTree(int l, int r) {
int ans = 0;
for (l += N, r += N; l <= r; l = (l + 1) >> 1, r = (r — 1) >> 1) {
if (l & 1) {
ans += sum[l];
}
if (!(r & 1)) {
ans += sum[r];
}
}
return ans;
}
vector<int> t;
int n;
void updTree(int pos, int val) {
for (pos += n; pos; pos >>= 1) {
t[pos] = max(t[pos], val);
}
}
int getTree(int l, int r) {
int ans = 0;
for (l += n, r += n; l <= r; l = (l + 1) >> 1, r = (r — 1) >> 1) {
if (l & 1) {
ans = max(ans, t[l]);
}
if (!(r & 1)) {
ans = max(ans, t[r]);
}
}
return ans;
}
const int nmax = 1e6 + 100;
vector<int> pos[nmax];
int cnt[nmax];
int distinct[nmax];
struct query {
int l, r, id;
bool operator<(const query& other) const {
return l < other.l;
}
};
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int q;
cin >> n >> q;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
t.assign(4 * n, 0);
for (int i = 0; i < n; ++i) {
pos[a[i]].pb(i);
}
vector<pii> pts;
for (int x = 1; x <= n; ++x) {
for (int i = 0; i + 1 < sz(pos[x]); ++i) {
int lf = pos[x][i], rg = pos[x][i + 1];
++lf, --rg;
if (lf > rg) {
continue;
}
int y = getTree(lf, rg);
//cout << x << " " << y << endl;
if (y == 0) {
continue;
}
pts.pb({n - y, x});
}
for (int p : pos[x]) {
updTree(p, x);
}
}
cnt[0] = 0;
distinct[0] = 0;
for (int x = 1; x <= n; ++x) {
cnt[x] = cnt[x - 1] + sz(pos[x]);
distinct[x] = distinct[x - 1] + (!pos[x].empty());
}
sort(all(pts));
int ptr = 0;
vector<query> queries(q);
vector<int> ans(q);
for (int i = 0; i < q; ++i) {
int l, r;
cin >> l >> r;
queries[i] = {n - l, r, i};
ans[i] = distinct[r] - distinct[l - 1];
}
sort(all(queries));
N = n + 1;
sum.assign(2 * N, 0);
for (int i = 0; i < q; ++i) {
while (ptr < sz(pts) && pts[ptr].first <= queries[i].l) {
updSumTree(pts[ptr].second);
++ptr;
}
ans[queries[i].id] += getSumTree(0, queries[i].r);
}
for (int i = 0; i < q; ++i) {
cout << ans[i] << "\n";
}
}
1864G-Magic Square
Idea : AquaMoon
Theorem 1: After a row shift, all numbers moved are in the correct column.
Proof 1: Suppose a number moved after a row shift is not in the correct column, if it is not in the correct row, it needs at least two more moves to its target position, otherwise it needs at least three more moves because the row cannot be shifted again.
Also, after a column shift, all numbers moved are in the correct row.
Theorem 2: If both row shift and column shift are performed, two rows cannot have equal shift distance.
Proof 2: If row $$$i$$$ is shifted by $$$x$$$ and column $$$j$$$ is shifted by $$$y$$$, regardless of their order, then there is a number with offset $$$(y, x)$$$. If row $$$i_1$$$ and row $$$i_2$$$ are shifted by $$$x$$$ and column $$$j$$$ is shifted by $$$y$$$, regardless of their order, then there are two numbers with the same offset $$$(y, x)$$$ (if two number coincide, it was moved at least three times).
In the same way, if both row shift and column shift are performed, two columns cannot have equal shift distance.
If after a row shift, all numbers moved are in the correct column, we call such rows available. Similarly, if after a column shift, all numbers moved are in the correct row, we call such columns available.
Theorem 3: If there is an available row and an available column at the same time, then there is no solution.
Proof 3: If row $$$i$$$ can be shifted by $$$x$$$ and column $$$j$$$ can be shifted by $$$y$$$, the number in $$$(i, j)$$$ has offset $$$(y, x)$$$. Assume that the number in $$$(i, j)$$$ is moved to $$$(i+y, j)$$$ and then to $$$(i+y, j+x)$$$. Row $$$i+y$$$ is shifted by $$$x$$$, no other row can be shifted by $$$x$$$. Consider the number in $$$(i,j+1)$$$, it needs to be shifted by $$$x$$$ in some row, so it must be moved to row $$$i+y$$$ before row $$$i+y$$$ shifts. Then the numbers in $$$(i, j)$$$ and $$$(i+1, j)$$$ have the same offset $$$(y, x)$$$. Similarly, if the number in $$$(i, j)$$$ is moved to $$$(i, j+x)$$$ and then to $$$(i+y, j+x)$$$, there is no solution.
We can use the following method to solve this problem:
For each row and each column, check if it is available.
If there are both available rows and available columns, there is no solution.
If no rows or columns are available, the matrix is already equal to the target one, or there is no solution.
If there are only available rows or available columns, their order doesn't matter, so if there $$$s$$$ choices, the answer should be multiplied by $$$s!$$$. Apply all available operations and check again.
Total complexity: $$$O(n^3)$$$ or $$$O(n^2)$$$ if maintaining row/column offsets in each row/column.
#include <bits/stdc++.h>
#define all(a) (a).begin(), (a).end()
#define sz(a) (int)(a).size()
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
const int mod = 998244353;
const int nmax = 600;
int fact[nmax];
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
fact[0] = 1;
for (int i = 1; i < nmax; ++i) {
fact[i] = ll(fact[i - 1]) * i % mod;
}
int tt;
cin >> tt;
while (tt--) {
int n;
cin >> n;
vector<vector<int> > a(n, vector<int>(n));
set<int> seta;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cin >> a[i][j];
seta.insert(a[i][j]);
}
}
assert(sz(seta) == n * n);
vector<vector<int> > b(n, vector<int>(n));
set<int> setb;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cin >> b[i][j];
setb.insert(b[i][j]);
}
}
assert(sz(setb) == n * n);
assert(seta == setb);
vector<int> vct;
for (int x : seta) {
vct.pb(x);
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
a[i][j] = lower_bound(all(vct), a[i][j]) - vct.begin();
b[i][j] = lower_bound(all(vct), b[i][j]) - vct.begin();
}
}
vector<pii> posa(n * n);
vector<pii> posb(n * n);
set<pii> off;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
posa[a[i][j]] = {i, j};
posb[b[i][j]] = {i, j};
}
}
bool valid = true;
for (int x = 0; x < n * n; ++x) {
pii p = posa[x], q = posb[x];
if (p.first != q.first && p.second != q.second) {
pii s = {(q.first - p.first + n) % n, (q.second - p.second + n) % n};
if (off.count(s)) {
valid = false;
} else {
off.insert(s);
}
}
}
if (!valid) {
cout << "0\n";
continue;
}
int cnt = 0;
ll ans = 1;
while (a != b) {
vector<pii> rows;
for (int i = 0; i < n; ++i) {
int shift = posb[a[i][0]].second;
bool ok = true;
for (int j = 0; j < n; ++j) {
int x = a[i][j];
if (posb[x].second != (j + shift) % n) {
ok = false;
break;
}
}
if (ok && shift) {
rows.pb({i, shift});
}
}
vector<pii> cols;
for (int j = 0; j < n; ++j) {
int shift = posb[a[0][j]].first;
bool ok = true;
for (int i = 0; i < n; ++i) {
int x = a[i][j];
if (posb[x].first != (i + shift) % n) {
ok = false;
break;
}
}
if (ok && shift) {
cols.pb({j, shift});
}
}
if (cols.empty() && rows.empty()) {
valid = false;
break;
}
if (!(cols.empty() ^ rows.empty())) {
valid = false;
break;
}
if (!rows.empty()) {
cnt += sz(rows);
ans *= fact[sz(rows)];
ans %= mod;
for (pii p : rows) {
int i = p.first;
int shift = p.second;
vector<int> v = a[i];
for (int j = 0; j < n; ++j) {
int x = v[j];
a[i][(j + shift) % n] = x;
posa[x] = {i, (j + shift) % n};
}
}
} else {
cnt += sz(cols);
ans *= fact[sz(cols)];
ans %= mod;
for (pii p : cols) {
int j = p.first;
int shift = p.second;
vector<int> v;
for (int i = 0; i < n; ++i) {
v.pb(a[i][j]);
}
for (int i = 0; i < n; ++i) {
int x = v[i];
a[(i + shift) % n][j] = x;
posa[x] = {(i + shift) % n, j};
}
}
}
}
if (!valid) {
cout << "0\n";
continue;
}
cout << ans << '\n';
// cout << cnt << " " << ans << "\n";
}
}
1864H-Asterism Stream
Idea : WrongAnswerOnTest3 Solution: Psychotic_D, amenotiomoi
Here is a basic $$$\Theta(n)$$$ dp solution.
Before that let $$$k = \frac{1}{2}$$$. At the same time, because a special geometric sequence $$$f(x)=ak^{bx}$$$ will be frequently used next, it is defined as $$$\{a,b\}$$$.
Let $$$f(x)$$$ be the expected number of moves needed if we start with $$$x$$$. Obviously, there is the following formula:
It's easy to see that for the interval $$$[n, 2n]$$$ value of $$$f(x)$$$ is $$$0$$$.
If for an interval $$$[2l,2r]$$$, it can already be represented by the sum of several $$${a,b}$$$, then it can be represented by a small number of new $$$\{a,b\}$$$ for all $$$f(x)$$$, where $$$x\in[l,r]$$$
First there is $$$f(r)=kf(r+1)+kf(2r)+1$$$. So, $$$r-1$$$ can be represented as $$$f(r-1)=k^2f(r+1)+ kf(2r-2)+k^2f(2r)+k+1$$$.
By analogy, one can get
by substitution, it can be shown as
Because $$$\{a,b\}$$$ of the interval where $$$f(r+1)$$$ is already known, the value of $$$f(r+1)$$$ can be calculated quickly. So, the first term of $$$f(x)$$$ can be represented as below:
Then the last term of $$$f(x)$$$, $$$\sum\limits_{i=0}^{r-x}k^i$$$ is sum of an ordinary geometric sequence. So, after applying the formula it can represented as $$$\{2,0\}+\{-k^r,-1\}$$$.
For the second term $$$\sum\limits_{i=0}^{r-x}k^{i+1}f(2x+2i)$$$, it has been assumed that $$$f(2x+2i)$$$ is $$$\sum\{a,b\}$$$, so split it into the following form (the derivation process depends on $$$k^{2b+1}\neq1$$$):
Because of the obvious combination law $$$\{a,b\}+\{c,b\}=\{a+c,b\}$$$, the number of its geometric series is linear with the number of recursions.
For $$$x\in[n,2n], f(x)=0$$$, which can be represented as $$$f(x)=\{0,0\}$$$, so this recursive rule can always be used, Until the $$$x\in[1,1]$$$ is obtained, to get the result.
The complexity varies depending on the implementation $$$\Theta(T\log^3n)$$$ or $$$\Theta(T\log^2n)$$$.
#include <bits/stdc++.h>
using namespace std;
#pragma GCC optimize("Ofast", "inline", "-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#define int long long
const int MOD = 998244353;
int n, k;
long long power(int x, int p)
{
if (p < 0)
return power(power(x, MOD - 2), -p);
int answer = 1;
x %= MOD;
while (p)
{
if (p & 1)
answer = answer * x % MOD;
x = x * x % MOD;
p >>= 1;
}
return answer;
}
void Delta()
{
cin >> n;
k = power(2, MOD - 2);
int l = n, r = max(1ll, (n - 1) * 2), n0 = 0, s;
vector<int> Q;
while (l > 1)
{
vector<int> P;
l = (l + 1) / 2;
r /= 2;
s = n0;
for (int i = 0, t = k - 1; i < (int)Q.size(); ++i)
{
s = (s + Q[i] * power(power(k, -(1ll << i)), r + 1)) % MOD;
t = t * t % MOD;
}
P.push_back(((power(k, r + 1) * s - power(k, r)) % MOD + MOD) % MOD);
for (int i = 0; i < (int)Q.size(); ++i)
{
P[0] += power(power(k, 1 - (1ll << (i + 1))) - 1, MOD - 2) * Q[i] % MOD * power(power(k, 1 - (1ll << (i + 1))), r + 1) % MOD * k % MOD;
P.push_back(((MOD - Q[i] * k % MOD * power(power(k, 1 - (1ll << (i + 1))) - 1, MOD - 2) % MOD) % MOD + MOD) % MOD);
}
P[0] += (MOD - n0) * power(k, r + 1) % MOD;
for (int &i : P)
i %= MOD;
Q = P;
n0 += 2;
}
s = n0;
for (int i = 0, t = k - 1; i < (int)Q.size(); ++i)
{
s = (s + Q[i] * power(power(k, -(1ll << i)), 1)) % MOD;
t = t * t % MOD;
}
cout << s << endl;
}
signed main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
cin >> T;
while (T--)
Delta();
}
1864I-Future Dominators
Idea : Psychotic_D, amenotiomoi
This problem is based on a method of online edge deletion and querying connectivity of a planar graph.
Firstly, if this vertex is not an articulation point, it will not cause any change in connectivity. Therefore, the algorithm needs to determine whether a certain vertex is an articulation point.
Thinking about using a data structure called union-find to keep track of the deleted points, we can identify a clear condition: if a vertex has two neighbors with the same union-find value among its $$$8$$$-connected neighbors, then it becomes an articulation point. This is easy to understand:
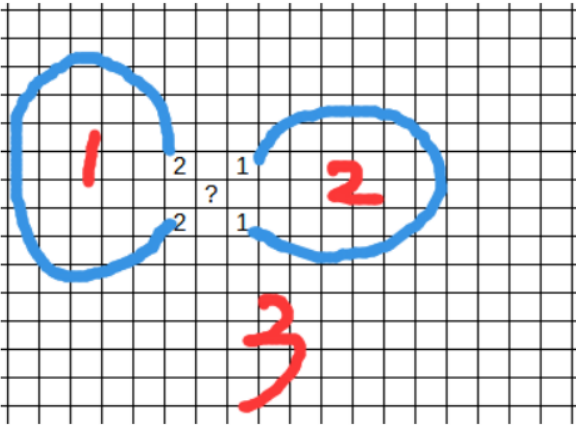
When the values in the union-find are the same, it means there's a loop forming, and this messes up how things are connected inside and outside the loop. But if all the values in the union-find are different, no loops will form, and we can find a way to connect these points to each other.
For points which are not articulation points, the greedy way to do it is to put the biggest number in the component of points that are already connected. This helps keep things organized and efficient.
Now, let's think about the case of articulation points. If we've already decided to put a $$$1$$$ in the connected group before the articulation point, it's pretty clear that, in order to get the largest overall value, we should put the $$$1$$$ in the smallest connected component. And the remaining connected components will then share the largest value. In other words, when we pick the largest number for one component, the largest numbers for the other components will decrease at the same time.
If we're sure that a particular component won't have the number $$$1$$$ placed in it, then the point we're looking at can only hold the value which is one more than the maximum value in the connected component formed by removing this point. It might sound a bit complicated, but I'll show you a picture to make it clearer.
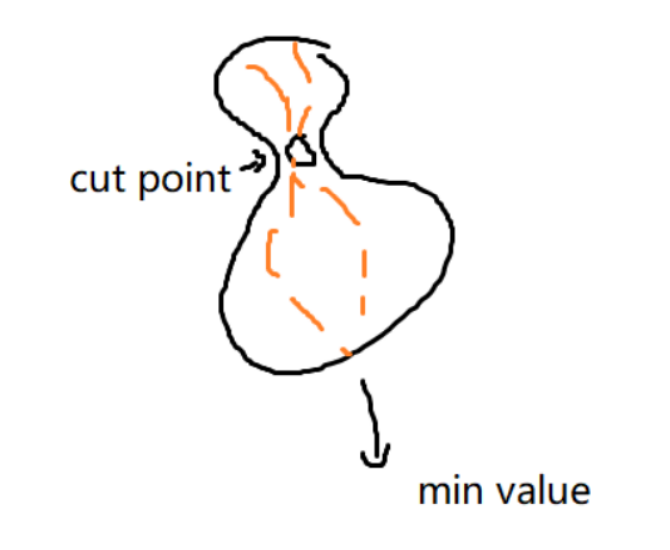
In simpler words, the value we put in that point is fixed. It's just the right amount to make sure it matches the sum of all the values in the connected group above it, instead of picking the smallest group. To make this work, we have to keep track of where the smallest value is located inside that connected component.
The method we discussed is quite slow, around $$$O(n^3)$$$. Now, let's talk about how to make it much faster, around $$$O(n^2 log n)$$$.
Firstly, for every cell, we keep a pointer that points to the information about its connected component. So, whenever we update any cell, the entire connected component gets updated automatically.
When dealing with articulation points, it's important to quickly update the pointer information. One effective way is to use a clever merging technique. This involves simultaneously performing a breadth-first search on multiple connected components. If only one connected component remains incomplete in the search, we immediately stop all calculations.
One of the things we need to do is to launch the BFS from the new connected components which arise after fixing a certain cell. In particular, we don't want to launch two parallel BFS which start in different cells but sooner or later are merged into one component. So among the $$$4$$$ side-neighbors of the cell being fixed, we need to segregate them based on the remaining connectivity, considering the removal of the current cell. To facilitate this segregation, we examine the 8 corner- or side-neighbors and analyze their DSU values. For instance, if all these DSU values are distinct from each other, it implies that the empty neighboring cells belong to a unified component.
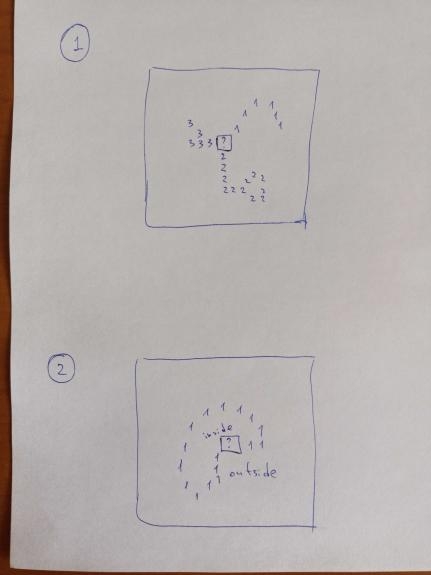
Conversely, if certain DSU values occur multiple times, it signifies the existence of a planar cycle that becomes linked through the cell being fixed. Consequently, cells within and outside this cycle must be assigned to separate connected components. To manage this, we iterate through pairs of $8-$neighbors sharing the same DSU value and classify the $4-$neighbors into those situated within the cycle and those outside it.
During the pointer update process, we handle smaller connected components by updating their pointers in a straightforward manner. For larger connected components, we retain their original pointers and make necessary adjustments. It's easy to show that this approach updates pointers efficiently (each time a connected group is encountered in the search, its size at least doubles). This helps us achieve a time complexity of $$$O(n^2 log n)$$$.
Next, we also need to determine whether two cells are part of the same connected component. This is necessary for calculating the situation represented in the previous image. This step is quite simple because we ensured earlier that pointers of different connected components are always different. So, all we need to do is compare the pointer values to check if two cells belong to the same connected component.
For the connected components that share the largest value, there are several ways to handle them. One approach is to use the *int data type for the maximum value, so changing one value directly changes the shared value. Another method is to use a vector to store the pointers that share the value, and when updating, you iterate through this vector to update them.
It's easy to prove that the maximum shared values can only exist in a maximum of $$$O(1)$$$ components simultaneously. This is because they only arise when cutting an articulation point in a connected component where the value is not $$$1$$$, and these components cannot merge together.
So, the total time complexity will be $$$O(n^2logn)$$$.
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize("Ofast","inline","-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
struct node {
int mx,sz;bool bg;
pair<int,int> mn;
vector<node*> cp;
void cln(){for(node* i:cp)i->cp.erase(find(i->cp.begin(),i->cp.end(),this));cp.clear();}
void fresh() {
if(!bg) return;
bg=false;int sum=0;node* lt=nullptr;
for(node* i:cp)if(i->bg){lt=i;sum++;}
if(sum==1){lt->mx=lt->sz;lt->bg=false;lt->cln();}
}
~node(){cln();}
};
int prevAns;
pair<int,int> fa[1002][1002];
pair<int,int> getfa(pair<int,int> x) {
if(fa[x.first][x.second]==x) return x;
return fa[x.first][x.second]=getfa(fa[x.first][x.second]);
}
void merge(pair<int,int> x,pair<int,int> y) {
pair<int,int> t=getfa(x);
fa[t.first][t.second]=getfa(y);
}
int n,q;
node* bk[1002][1002];
bool vis[1002][1002];
vector<pair<int,int>> dxy={{-1,-1},{-1,0},{-1,1},{0,1},{1,1},{1,0},{1,-1},{0,-1}},xy={{-1,0},{0,1},{1,0},{0,-1}};
void Delta() {
cin >> n >> q;
bk[1][1]=new node{n*n,n*n,false,{0,0},{}};
for(int i=0;i<=n+1;++i)
for(int j=0;j<=n+1;++j) {
fa[i][j]={i,j};
if(i==0||j==0||i==n+1||j==n+1) {
fa[i][j]={0,0};
vis[i][j]=true;
bk[i][j]=nullptr;
} else {
bk[i][j]=bk[1][1];
vis[i][j]=false;
}
}
prevAns=0;
while(q--) {
int x,y,cnt=1;cin >> x >> y;
x^=prevAns;
y^=prevAns;
pair<int,int> Q[8];
int P[4]={0,0,0,0};
for(int i=0;i<8;++i)
Q[i]=getfa({x+dxy[i].first,y+dxy[i].second});
for(int i=0;i<8;++i)
for(int j=1;j<8;++j)
if(Q[i]==Q[(i+j)%8]) {
cnt++;
for(int k=(i+1)%8;k!=(i+j)%8;k=(k+1)%8)
if(k%2==1)
P[k/2]+=1ll<<cnt;
break;
}
vis[x][y]=true;
for(pair<int,int> i:dxy)
if(vis[x+i.first][y+i.second])
merge({x,y},{x+i.first,y+i.second});
bk[x][y]->fresh();
if((P[0]&P[1]&P[2]&P[3])==max({P[0],P[1],P[2],P[3]})) {
prevAns=bk[x][y]->mx;
cout << prevAns << ' ';
bk[x][y]->mx--;bk[x][y]->sz--;
for(node* i:bk[x][y]->cp) i->mx--;
if(bk[x][y]->sz==0) delete bk[x][y];
} else {
vector<pair<int,int>> s[4];
queue<pair<int,int>> q[4];
pair<int,int> id[4];
int cnt,dc=0;
{
vector<int> R;
for(int i=0;i<4;++i) R.push_back(P[i]);
sort(R.begin(),R.end());
R.resize(unique(R.begin(),R.end())-R.begin());
cnt=R.size();
for(int i=0;i<4;++i)
P[i]=lower_bound(R.begin(),R.end(),P[i])-R.begin();
}
for(int i=0;i<cnt;++i) {
for(int j=0;j<4;++j)
if(P[j]==i&&!vis[x+xy[j].first][y+xy[j].second]) {
id[i]={x+xy[j].first,y+xy[j].second};
if(!vis[id[i].first][id[i].second]) {
q[i].push(id[i]);
s[i].push_back(id[i]);
vis[id[i].first][id[i].second]=true;
dc++;
}
break;
}
}
while(dc>1)
for(int i=0;i<4;++i)
if(q[i].size()!=0) {
pair<int,int> t=q[i].front();q[i].pop();
for(int j=0;j<4;++j) {
pair<int,int> p={t.first+xy[j].first,t.second+xy[j].second};
if(!vis[p.first][p.second]) {
q[i].push(p);s[i].push_back(p);
vis[p.first][p.second]=true;
}
}
if(q[i].empty()) --dc;
}
vector<int> sm,bg;node* tp[4];
if(bk[x][y]->mx==bk[x][y]->sz) {
if(dc==1) {
for(int i=0;i<4;++i)
if(!q[i].empty()) bg.push_back(i);
else if(!s[i].empty()) sm.push_back(i);
for(int i:sm) {
tp[i]=new node{bk[x][y]->mx,(int)s[i].size(),false,{x,y},{}};
for(pair<int,int> j:s[i])
bk[j.first][j.second]=tp[i];
}
for(int i:sm) {
for(int j:sm)
if(i!=j) tp[i]->cp.push_back(tp[j]);
bk[x][y]->sz-=s[i].size();
}
prevAns=bk[x][y]->sz;
cout<< prevAns << ' ';
bk[x][y]->sz--;bk[x][y]->mx=bk[x][y]->sz;
} else {
int mxz=0;
for(int i=0;i<4;++i)
if(!s[i].empty()) {
sm.push_back(i);
mxz=max(mxz,(int)s[i].size());
}
prevAns=mxz+1;
cout << prevAns << ' ';
for(int i:sm) {
tp[i]=new node{bk[x][y]->mx,(int)s[i].size(),(int)s[i].size()==mxz,{x,y},{}};
for(pair<int,int> j:s[i])
bk[j.first][j.second]=tp[i];
}
for(int i:sm)
for(int j:sm)
if(i!=j) tp[i]->cp.push_back(tp[j]);
delete bk[x][y];
}
} else {
vector<node*> ar;vector<int> lt,ult;
if(dc==1) {
int sult=1,ty=bk[x][y]->mx;
pair<int,int> pmn=bk[x][y]->mn;
bk[x][y]->mn={x,y};bk[x][y]->sz--;
for(int i=0;i<4;++i)
if(!s[i].empty()) {
if(!q[i].empty()) {
bg.push_back(i);
tp[i]=bk[x][y];
}
else {
tp[i]=new node{bk[x][y]->mx,(int)s[i].size(),false,{x,y},{}};
sm.push_back(i);
bk[x][y]->sz-=(int)s[i].size();
for(pair<int,int> j:s[i])
bk[j.first][j.second]=tp[i];
}
}
pair<int,int> tmp=pmn;
for(pair<int,int> i:xy) {
node* t=bk[i.first+tmp.first][i.second+tmp.second];
if(t!=nullptr&&pair<int,int>{i.first+tmp.first,i.second+tmp.second}!=pair<int,int>{x,y}) {
ar.push_back(t);
}
}
vector<node*> cp=bk[x][y]->cp;
for(node* i:cp) i->cp.erase(find(i->cp.begin(),i->cp.end(),bk[x][y]));
bk[x][y]->cp.clear();
for(int i=0;i<4;++i) {
if(!s[i].empty()) {
if(id[i]==tmp||find(ar.begin(),ar.end(),bk[id[i].first][id[i].second])!=ar.end()) {
tp[i]->mn=pmn;
lt.push_back(i);
} else {
ult.push_back(i);
sult+=tp[i]->sz;
}
}
}
for(int i:ult)
for(int j:ult)
if(i!=j) tp[i]->cp.push_back(tp[j]);
for(node* i:cp) {
for(int j:lt) {
i->cp.push_back(tp[j]);
tp[j]->cp.push_back(i);
}
i->mx-=sult;
}
prevAns=ty-sult+1;
cout << prevAns << ' ';
for(int i:lt) {
for(int j:lt)
if(i!=j) tp[i]->cp.push_back(tp[j]);
tp[i]->mx-=sult;
}
} else {
pair<int,int> pmn=bk[x][y]->mn;
int sult=1;
for(int i=0;i<4;++i)
if(!s[i].empty()) {
tp[i]=new node{bk[x][y]->mx,(int)s[i].size(),false,{x,y},{}};
for(pair<int,int> j:s[i])
bk[j.first][j.second]=tp[i];
}
pair<int,int> tmp=bk[x][y]->mn;
for(pair<int,int> i:xy) {
node* t=bk[i.first+tmp.first][i.second+tmp.second];
if(t!=nullptr&&pair<int,int>{i.first+tmp.first,i.second+tmp.second}!=pair<int,int>{x,y})
ar.push_back(t);
}
for(int i=0;i<4;++i)
if(!s[i].empty()) {
if(id[i]==tmp||find(ar.begin(),ar.end(),bk[id[i].first][id[i].second])!=ar.end()) {
tp[i]->mn=pmn;
lt.push_back(i);
} else {
ult.push_back(i);
sult+=(int)s[i].size();
}
}
for(int i:ult)
for(int j:ult)
if(i!=j) tp[i]->cp.push_back(tp[j]);
for(node* i:bk[x][y]->cp) {
for(int j:lt) {
i->cp.push_back(tp[j]);
tp[j]->cp.push_back(i);
}
i->mx-=sult;
}
for(int i:lt) {
for(int j:lt)
if(i!=j) tp[i]->cp.push_back(tp[j]);
tp[i]->mx-=sult;
}
prevAns=bk[x][y]->mx-sult+1;
cout << prevAns << ' ';
delete bk[x][y];
}
}
for(int i=0;i<4;++i)
for(pair<int,int> j:s[i])
vis[j.first][j.second]=false;
}
bk[x][y]=nullptr;
}
set<node*> _;
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
_.insert(bk[i][j]);
for(node* i:_)
if(i!=nullptr) delete i;
cout << endl;
}
signed main() {
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin >> T;
while(T--) Delta();
}
Feel free to ask if you have any questions! (*╹▽╹*)










Is there any mathematical solution for A ?
For example : I tried to figure out whether the gap=y-x-1 is >= required_gap. Where required_gap = ((n-2)*(n-1))/2 ( n-2 because nth and 1st element are already set ) I tried this way but failed pretest 2.
check my A
Why do people downvote even for a fair question?
Yes, I solved it somewhat mathematically.
You can check my solution here https://codeforces.me/contest/1864/submission/220530206
Try to get better
lol you have less rating than him
OK
unrelated
I'm so sorry
thats rude
I have no idea what the editorial is talking about for H. I thought it was a "berlekamp massey go brrrr" problem.
Can you elaborate on your solution?
Short version:
By linearity of expected value, we can sum up the probability of reaching each state with value < N and that's the answer
dp[i][j] = probability of reaching a state that sum operations summed up to at most j and there were exactly i operations of multiply by 2. In other words, exactly i multiply by 2 operations and the number is <= 2^i + j.
dp[i][j] = (dp[i][j-2^i] + dp[i-1][j]) / 2
The answer is sum dp[i][N-2^i] for every i.
Define F_i[n] = dp[i][N % (2^i) + n * 2^i]. F_0 is a recurrence (F_0[n] = F_0[n-1] / 2 + 1).
F_i[n] = (F_i[n-1] + dp[i-1][N % (2^i) + n * 2^i]) / 2 = (F_i[n-1] + F_(i-1)[a_i + 2 * n]) / 2 for some a_i that is 1 or 0, because N % 2^i is either N % 2^(i-1) or N % 2^(i-1) + 2^(i-1).
Hope that the following works:
R'[n] = R[a + b * n] for constant a, b. If R is a recurrence of degree D, R' is also a recurrence of degree D.
R'[n] = R'[n-1] + R[n]. If R is a recurrence of degree D, R' is a recurrence of degree D+1.
it shouldn't be hard to prove that. I think I'm able to prove it using generating functions.
then the solution is: compute the first 2*i values of F_i using the first 4*i values of F_(i-1) then interpolate the recurrence using berlekamp massey.
Video tutorial for problems A&B&C explained: https://youtu.be/y5QoCUF7hpQ IN ENGLISH Thought would be useful
fast editorial. very thank you.
Another way to understand problem C :
If we are faced with number $$$2n$$$, take a sequence of operations that takes $$$n$$$ to $$$1$$$, multiply every factor by $$$2$$$ so that you get a sequence that takes $$$2n$$$ to $$$2$$$, then decrease by $$$1$$$. If we have number $$$2n + 1$$$, just decrease by $$$1$$$.
We can see that no divisor will appear more than twice because of the multiplications by $$$2$$$ that make them bigger as it goes.
It in fact creates the same sequence as the one in the editorial, but that's how I found it anyway
Sir I had applied the same but there is a wrong answer..
Here's my submission if you want to compare :
https://codeforces.me/contest/1864/submission/220544686
In problem B, is there a proof that after some series of these 2 transformations any two adjacent elements will be swapped?
Notice that every element with the same indices modulo $$$2$$$ are already "congruent" (i.e. can be swapped over freely). Now, lets say the original string was $$$abcdefghij$$$. If we apply the same operations with the editorial, the string becomes $$$fedcbaghij$$$, and then $$$fgabcdehij$$$. See how $$$f$$$ originally had an even index, but now an odd index. Now after we swap things over, we can make $$$abcdegfhij$$$, only leaving this pair of $$$f$$$ and $$$g$$$ swapped. We can generalize this to swap any two adjacent indices. The rest of the proof is left for the reader.
Really cool round, enjoyed every problem C-F! Thank you very much authors!
Why TLE for problem D?
Submission
It gets AC in 64-bit C++, or if you add the fast-IO line which is unfortunate :/. See 220609340, you should keep that line in pretty much all submissions. (
ios_base::sync_with_stdio(false); cin.tie(NULL);)thanks
Anyone solving problem D with $$$O(n^2logn)$$$ segtree solution? Got TLE but it should pass n = 3000... Perhaps my segtree template sucks.
You can check my sumbission 220585884 It passed all the tests however very close to TLE. At first, I thought it should work without any problems, but now I understand I'm lucky it didn't fail
Removing the lazy part of this template is enough to make it work 220620036 (this works because you are only adding to ranges of length 1, so no actual lazy propagation takes place).
It is also storing / updating node lengths everywhere, which is also not needed, and removing it would probably speed it up even further.
It's was a great round! Thanks for editorial. Problem C was pretty nice
I got TLE on test 49 in F(220571360), I can pass in less than 1000ms by using fread(220608103). But test 48 need to read more things than test 49. What's the reason?
So do I. Should I stop using cin/cout from now on?
I got the same TLE due to using std::sort. It might be the first time I'm seeing a NlogN intended solution not allowing std::sort.
I don't think your TLE is due to std::sort. Your code passes with a small change (seems to be the same thing as here).
using GNU C++14 can pass in 1560ms(220632696), using GNU C++20 (64) got TLE in 4 seconds(220632734)?
bruh sounds so weird
When im upsolving problems i think that cpp20 is much faster that cpp14? See my submissions on 1265E ^^
Hay, I also met the same issue. And I also tested different IO methods and different implementations of segment tree. The result is on this blog. I don't know the reason, but you could have a look if you are interested.
Can someone share their O(sqrt(x)) solution for problem C? I had no clue that bit manipulation was to be used here.
I think I was able to get a very readable solution: https://codeforces.me/contest/1864/submission/220570492
https://codeforces.me/contest/1864/submission/220567377
my idea seems stupid ,but it's right.
I've rewritten your solution in a more straightforward way: https://codeforces.me/contest/1864/submission/220633771
though, anyone has any ideas/intuitions why it works?
$$$O(T \sqrt A)$$$
Why does this submission for B fails,i was doin, exactly same as of tutorial,
https://codeforces.me/contest/1864/submission/220591195
if(n & 1) u print new line
but u don't print new line in other case, where next query solution merges with that query
If $$$k$$$ is odd and $$$n$$$ is even, you don't print a newline character at the end:
Does anything change in problem B with n=k? I couldn't think of a difference
For odd $$$k$$$ nothing indeed changes: one can sort even and odd parts separately and nothing more can be done.
For even $$$k$$$ the method, provided in the editorial, fails. There don't exist two segments of kind $$$[i; i + k - 1]$$$ and $$$[i + 1; i + k]$$$. Now it's not always possible to change parity of two characters (to move one from odd to even position, and another in the opposite direction). The only possible option is to do it in bulk, i. e. change parities of many characters at once. That could fail to lead to totally sorted string.
One can consider a string like $$$\texttt{cdba}$$$ and $$$k = 4$$$. It is possible to change it to $$$\texttt{cabd}$$$, $$$\texttt{bdca}$$$, or $$$\texttt{bacd}$$$ using only swaps. Now you see that $$$\texttt{abcd}$$$ is unreachable (and so is $$$\texttt{dcba}$$$), though $$$k$$$ is even.
Thanks, you're right. I should've tried to observe with a small example.
The odd and even positions could be swapped altogether in that case, but not completely mixed. Interesting!
Maybe my solution for D using bitsets would be easier to understand for some people
I'm not really getting the solution to D. I don't understand why prefix sums are mentioned and how they are used. The code did not clarify anything, it just confused me more. It would be very helpful if someone could give a more detailed explanation.
See https://codeforces.me/blog/entry/119772?#comment-1062644
Thank you very much, now it's clearer.
A more understandable solution to H, and didn't require too much knowledge or math.
First, we can consider subtracting $$$1$$$ from $$$n$$$ or dividing $$$n$$$ by $$$2$$$, and compute the expected step to make $$$n$$$ be $$$0$$$. We can build a recurrence $$$f(n) = 1 + \frac{1}{2} (f(n - 1) + f(\lfloor n/ 2 \rfloor))$$$. And the answer to the original problem is $$$f(n - 1)$$$.
It seems it's hard to compute $$$f(n)$$$ by some matrix or the linear recurrence trick. But here is the magic, you can maintain $$$b_{n} = [f(n), f(\lfloor n/2 \rfloor), f(\lfloor n/4 \rfloor), \dots, 1]^T$$$. So we can build the transition from $$$b_{n-1}$$$ to $$$b_n$$$. And it's not hard to see, that the transition matrix only depends on the number of trailing zeros of $$$n$$$ in its binary representation. The answer is $$$\prod_{i=1}^n M_{ctz(i)}$$$.
We can precompute $$$\prod_{i=1}^{2^k} M_{ctz(i)}$$$ in $$$O(\log^4 n)$$$, and solve each query in $$$O(\log^3 n)$$$.
Submission: 220569504
Wow, very cool! Thank you for sharing.
I think my solution is very similar to yours, though I do not 100% understand your sol. My solution represents the dp like this: $$$f(x + 1) = 1 + \frac{1}{2}(f(x) + f(\left \lceil{\frac{x}{2}}\right \rceil)$$$ (exactly the same as yours essentially) with a restriction of I will assume that $$$x \equiv 0 \;(\bmod\; 2)$$$. Then I calculate a new function $$$f(x + 2) = 1 + \frac{1}{2}(f(x + 1) + f(\left \lceil{\frac{x + 1}{2}}\right \rceil).$$$ Then I will assume that $$$x \equiv 0 \;(\bmod\; 4)$$$ and rewrite the formula like this: $$$f(x + 2) = 1 + \frac{1}{2}(f(x + 1) + f(\left \lceil{\frac{x}{2}}\right \rceil + 1).$$$ Note that now both of the recurrences can be substituted with the first function, and when all simplified it leads to $$$f(x + 2) = 2 + \frac{1}{4}(f(\left \lceil{\frac{x}{4}}\right \rceil) + 2f(\left \lceil{\frac{x}{2}}\right \rceil) + f(x))$$$. Then again I will assume that $$$x \equiv 0 \;(\bmod\; 8)$$$ and re-expand the formula and repeat. This leads to log n different functions that can jump from $$$f(x) \rightarrow f(x + 2^{k})$$$ when $$$x \equiv 0 \;(\bmod\; 2^{k})$$$ (given that you know $$$f(\left \lceil{\frac{x}{2^{i}}}\right \rceil)$$$ for all i <= k).
Submission: 220629661
It really took me a long time to wrap my head around the pattern between expansion and how to code it up but I think it is quite beautiful how apply somewhat arbitrary modulo restrictions onto the equation allows for kind of a "binary exponentiation" trick.
why your f(n) = 1 + (1/2) * (f(n — 1) + f(n / 2)) ? why do not you consider the case which n is a add number ?
He shifted all the numbers down by one, so the floor division actually becomes ceil diving.
The method of undetermined coefficients (待定系数法) also works: https://codeforces.me/blog/entry/119850
Why is $$$f(n-1)$$$ equal to the answer? I still can't prove this after few months :(
Problem C is Preety Good. I didn't get any approach during contest I solved A, not able to B , C then i got D :) Though rank is very bad but solved D :)
I have another solution to E
Instead of creating a bit trie I create an array a[n][logA], where a[i][0] = v[i] for each i and a[i][j] = a[i][j — 1] >> 1 for each j 0 < j < logA, so lets look at number of such elements a[k][j] that a[i][j]=a[k][j] and a[i][j-1] != a[k][j — 1]: these elements have the same highest elements (and same number of '1' on the same places). So we can calculate the answer easier in O(nlogA) time and memory
How do we sort ACBDE TO ABCDE with k as 4?
An alternative solution of 1864E - Guess Game
From the very beginning let us sort our sequence $$$s$$$.
For two integers $$$a$$$ and $$$b$$$ denote by $$$f(a, b)$$$ the number of $$$1$$$-s in the largest common prefix of $$$a$$$ and $$$b$$$. Then the answer is
Denote
The key step is to note that since $s$ is sorted, then for $$$i < j$$$ we have
Therefore, we obtain
We can compute the sum of minimums of all subsegments of $a$ with $$$O(n)$$$ time complexity (for each element $$$a_i$$$ we should just find the nearest elements from left and right that are less then $$$a_i$$$). The both remaining terms are obviously also linear.
Code: 220611319
I solved D using the data structures. Let's consider that we have already found all the cells that will have the value $$$1$$$ and will have row index smaller than $$$x$$$. Let's denote the number of that cells as $$$currentCount$$$. Now, we want to find all the cells equal to $$$1$$$ in the row $$$x$$$.
Let's consider the cell $$$(x, y)$$$, and understand which cells can force the cell $$$(x, y)$$$ to flip its value. The value in the cell $$$(x, y)$$$ will be equal to the initial value in the cell $$$(x, y)$$$ plus the number of cells $$$(i, j)$$$ (mod 2) satisfying the following condition:
For the second condition, we can note that the equation is met either for $$$x - i \geq y - j$$$ or for $$$x - i \geq j - y$$$, since we know that $$$x - i > 0$$$ and $$$min(y - j, j - y) \leq 0$$$. So we need to find the number of cells, for which both equations are met:
So we can keep two Fenwick trees, and for each cell in the first Fenwick tree add $$$1$$$ in position $$$i - j$$$ and for the second one in position $$$i + j$$$.
Now, the new value for the position $$$(x, y)$$$ will be equal to the following:
where $$$get1(x)$$$ is equal to the sum of values in the first Fenwick tree, for which the indices are smaller than or equal to $$$x$$$. $$$get2(x)$$$ is the same for the second Fenwick tree.
Yaa I do the same. You can still improve it like instead of 4 values in the expression use diagonals to get the value.I do it this way. By seeing as diagonal we remain with just 2 values
Why should we subtract currentCount?
Because for each cell we may count it twice, and we guarantee know that we count each cell at least once. Our goal is to calculate only the cells for which both equations are met, because of it we subtract $$$currentCount$$$.
Shouldn't currentCount count the answer so far above the current row, which may contain flipped cells not affecting cell (x, y)? Why remove cells not even flipping current one?
Because for each cell we know that at least one of these equations is true:
$$$x - i$$$ is always greater than 0, while the minimum of $$$y - j$$$ and $$$j - y$$$ is always smaller than or equal to 0.
Oh, got it now, that's smart, thanks for the explanation
Tutorial of F: Consider all adjacent equal pairs $$$(l, r)$$$, and $$$m$$$ is the minimum element between $$$(l, r)$$$.
$$$m$$$ should be the maximum element between $$$(l, r)$$$ satisfying $$$m < a_l$$$
That confused me as well
Sorry for the mistake! Fixed. Thank you (〃'▽'〃)o
It seems like you didn't fully fix it. Now the tutorial says:
... and $$$m$$$ is the maximum element between $$$(l, r)$$$
You changed minimum to maximum, but didn't add the constraint $$$m < a_l$$$
Oh thank you! Fixed (〃•ω‹〃)
An O(nlog(max(ai)) solution for E, without tries.
shouldn't 30*N*log(N) pass the time limit? can someone check the solution
for prefixes i am converting them to number and storing in map
I didn't read the code too carefully but you can try to check whether
mp[x]exists before doing operations like+= mp[x]. This prevents the map from creating extra elements. I also had TLE with map and this helped.Yep that worked for me too.
The word "graph" appears only once in this tutorial, for 9 problem
How can I "Reduce $$$x$$$ to $$$2L$$$." in problem C?
for some x, say 19 whose binary representation is 10011 = 2^4 + 2^1 + 2^0. You can see that 2^1 divide 2^4, 2^0 divide 2^4, 2^0 divide 2^4. So the answer is you just minus the rightmost bit to x, in this case, is 2^0 and 2^1 until x has only one bit in binary representation.
P/S: Sorry for my bad English. Hope you understand this explanation
In F,
Can someone explain how sweeping lines are used here? A link would also be appreciated.
I think my solution implements that 220623962. sweepline used for dectime.
The first part of the solution is finding $$$m$$$ (the maximum value in $$$(l, r)$$$ that is less than $$$a_l = a_r$$$) for all adjacent equal pairs $$$(a_l, a_r)$$$. I did this using a segment tree and stored the pairs $$$(m, a_l)$$$. Now, you need to count the number of pairs that satisfy $$$m < L \leq a_l = a_r \leq R$$$ for each query.
Sort the queries by increasing the left endpoint and also sort the pairs found earlier. Now, you can do sweepline and add the values of $$$a_l = a_r$$$ to an ordered set once $$$m$$$ is less than the current query's $$$l$$$. The answer for each query is the position of the upper bound of $$$r$$$ in the set.
220616946 sorry if the code is a bit messy.
I think I see it, thank you.
Another implement for D whose time complexity is O(n^2) but only O(n) space 220627524. The logic in this code may cause you confused, in this case, ask me(and vote)
O(n) space? It takes O(n^2) memory just to store the matrix lol.
Sorry for my mistake. I had to fix it and now this code uses only 156KB of memory 220627524
Why we need to store the minus and the add in different arrays. Should that not be possible using a single prefix sum array like what I have done in this solution. It is giving WA but I am not able to understand why it is wrong. Can you please help me?
I don't know how to explain this clearly. But the key is the minus and the add extend in a different direction
Hey, can you explain your solution? It really would be helpful. Thanks
Problem F is somewhat similar to this: http://www.usaco.org/index.php?page=viewproblem2&cpid=1116 (It is the same problem but [l, r] matters on position rather than value. The basic idea (incrementing R and maintaining L in a fenwick tree / segment tree) persists in this problem too which I find to be pretty cool (The only addition is that you need to use a min segment tree to determine the ranges to add).
Feedback on the problems:
A and B: Fine easy problems. Not especially interesting, but not too bad (and quick enough that I was able to move on to the more exciting problems without too much delay).
C: Good easy problem. In some sense, the observation to use powers of two wasn't especially motivated, but for problems like this I often find it helpful to try to reduce the problem to some special case I know how to handle easily, so in that sense reducing $$$n$$$ to the next lower power of two felt like a reasonable thing to do.
D: Not terrible, but not my favorite problem ever. The idea to go top to bottom and flip cells that needed to be flipped along the way was fairly intuitive, and so it felt like most of the task was just working out details.
E: Good problem. I always enjoy this kind of logic puzzle, and I found both solving the problem and implementing the solution to be fairly satisfying.
F: Nice DS problem. The idea is both well-motivated and elegant, and all in all the implementation isn't too bad.
G: I enjoyed this problem very much, with the reservation that I think the statement was very contrived. It felt like the conditions in the problem basically came from having the solution in mind and trying to stretch the setting of the problem to fit it. Once I parsed the task, though, I really enjoyed the process of working on it (even though I wasted time in contest implementing a completely incorrect idea, then failed to debug my correct solution before the end of the round :p). It was very satisfying to gradually understand the setup of the problem better until I was finally able to make the observations necessary to solve the problem.
H: Decent problem. The setup is nice, but I wasn't a huge fan of the main observation (realizing that the relevant sequence can be expressed as sums of geometric sequences) because it didn't feel like I was unlocking some deep structure of the problem--instead, it felt as though I was doing the bare minimum to get the problem to fit into some high-powered technology (e.g. Berlekamp-Massey as other commenters have noticed; I was able to use Gauss-Jordan elimination to achieve essentially equivalent effect).
I haven't paid close attention to the preparation (e.g. I didn't check to see how many FSTs there were), and there was obviously an issue with the original test data in D, but overall I enjoyed the problems (especially EFG) and the round as a whole (despite performing below my standards and taking a substantial rating loss). Thanks to the authors!
Thanks for your precious feedback.
F constraints are too large for seemingly no reason imo. Too many people had trouble because of obscure differences between the 64bit compiler and 32bit one. I've still not seen a decent explanation about what's happening.
https://codeforces.me/blog/entry/119512?#comment-1062631
What about it? That blog doesn't contain sufficient explanation about what's happening, just some guesses of what might cause it.
Actually, I'm not the author of problem F, so maybe AquaMoon can help you ...
I thought C was fairly motivated if you reach the solution recursively such as a commenter did above: https://codeforces.me/blog/entry/119772?#comment-1062597
If only the constraint for k in C was 64, I would've done it faster. Anyways, nice problems!
Can someone explain me D?
How are we achieving the required conditions? And it is my request to authors to please be consistent. It is easier to understand the code when it is based on tutorial.
Let me explain a bit informally.
We greedily look from above, inverting every cell with $$$1$$$ by using the operation right on that cell. This is because, if we do not use the operation on this cell, we cannot affect this cell at all afterwards, therefore we must use the operation on this cell.
Now for how we will simulate the operations. Try rotating the matrix by $$$45$$$ degrees, and now the range of the operations will be a rectangle (though clipped out due to the borders), which is a very good situation to use a 2D prefix sum on. This should help you to understand the rest of the solution.
Still not able to understand the simulation. I am finding it difficult to imagine it. Can you explain me what the editorial code is trying to do? I will try understanding it using dry testing.
you can look at my code which does the same thing but in a less contrived way https://codeforces.me/blog/entry/119772?#comment-1062644
Great contest!~ qwq i love the problem D and i think the expectation problem E is also great. by the way congratulate to le0n for getting to grandmaster~
I have a different solution for D. Suppose I am at (x,y) and I want to check the parity of the number of cells before it which have affected this cell. Observe that, if a cell "covers" (x-1, y) (a cell covers a cell (a,b) if the diagonal lines coming out of it enclose (a,b)), then it also covers (x,y). Now, what are those points which cover only (x,y) but do not cover (x-1,y)? They are precisely those whose right diagonal (line with slope -1) passes through (x-1,y-1) and (x,y), and those whose left diagonal (line with slope 1) passes through (x-1, y+1) and (x,y). So, we need to store and do the following updates: For the previous row, store how many times (x-1, y) was operated upon, add its parity, and also add the parity of the number of operated cells which are diagonal to (x,y), which can be stored in a map using the fact that the sum/difference of the indices on the diagonals remains constant. https://codeforces.me/contest/1864/submission/220595343
I loved problem D proposed by AquaMoon and obviously the problem H proposed by you buddy amenotiomoi, and the Editorial justifies it <3
I am so delighted that you love my problem!~o(〃'▽'〃)o
Its obvious for me to like ヽ(´▽`)ノ <3
can anyone tell me this why https://codeforces.me/contest/1864/submission/220617780 solution of b is giving time complexity?
Use fast IO, add this
ios :: sync_with_stdio(0), cin.tie(0), cout.tie(0);in your main, then you'll pass, read more about it here : https://www.geeksforgeeks.org/fast-io-for-competitive-programming/I was having fun solving those problems. Enjoyable round.
I thought about B's bonus and came out with a solution:
Solve the problem with $$$k=3$$$. Then flip the string. Solve the problem again. Then find the minimum among the two.
If $$$n\le 2$$$, then you can just sort the string.
how tf can people have negative rating when in this contest i didn't solve a single problem but got +112 and got to +875 ?
https://codeforces.me/blog/entry/77890?locale=en
So you actually got 112-250 = -138.
By mistake, I solved F for index range queries, instead of value range. Does anyone have link to that kind of a problem ?
Problem linked here: https://codeforces.me/blog/entry/119772?#comment-1062685.
Thanks man!
i know how D works but i dont understand the prefix sum part, i have been tried for many hours and i couldn't figure it out, please give me some help :(
A
1in the current line can result in111in the next line, and11111in the line after next. Since these number of1s are O(n), we can try to reduce it to O(1) by using prefix sums.i understood the 11111 part, but struggling with O(1) prefix sum update :(, ill try my best to figure it out, thanks for paying attention
F Why the maximum element between (l,r) and max<L (I guess it's value L) can counted
in problem B what is the proof that with even K it is always possible to sort the elements in order? can any one help me with that...
Swap $$$(s_{i}, s_{i+2})$$$ means we can sort all the chars in odd and even positions. If $$$k$$$ is even we can change the parity of any char we want (i.e. from odd to even and from even to odd) thus we can sort all string.
but why does size of k does not matter suppose if n=6 and k=4 then how can we sort them
I was trying explaining it by myself, but editorial is better. In the first pic the red is what have changed, blue is what remaining the same. So we can just swap the modulo 2 of two adj. indexes we want, and with swap $$$(s_{i}, s_{i+2})$$$ we can place any chars we want. For you i made the same with $$$n = 6$$$ and $$$k = 4$$$.
I still don't get that, I tried to apply this to dfcbea using k=4 but didn't get abcdef. How can I?
1pic 2pic
I understand how to prepare and utilize 2D prefix sums for range queries, as well as how to prepare and utilize 1D difference arrays for range updates. However, Problem D here seems to require 2D difference arrays, which I haven't quite figured out yet, and the editorial seems to be rather vague. Can anyone please provide any resources to learn about 2D difference arrays and/or elaborate on the details for it?
Well, 2D prefix sums and 2D difference arrays are essentially the exact same. Let's say you add 1 to p[x][y]. When computing the prefix sum of p, you would have added 1 to all a[i][j] where i >= x and j >= y. Using this in a similar method to how 2d prefix sums allows you to do rectangular updates.
Example:
p[0][0]++;
p[2][0]--;
p[2][2]++;
p[0][2]--;
if you compute the prefix sum of p, you will end up with
1 1 0
1 1 0
0 0 0
(top-left is (0, 0))
Bonus for F: try to solve it as if it were an interactive problem, i.e. you must answer a query in order to read the next one.
Just like in the editorial, we iterate through all $$$i$$$ from $$$1$$$ to $$$n$$$ and for all adjacent pairs $$$(l, r)$$$ where $$$a_l=a_r=i$$$, we shall find the maximum element $$$m$$$ between $$$(l, r)$$$ that satisfies $$$m<i$$$. We then add the value $$$m$$$ to a vector $$$v$$$. As we do this, for each $$$i$$$ we can memorize $$$start_i$$$ = the index of the first number in $$$v$$$ that corresponds to a pair $$$(l, r)$$$ where $$$a_l=a_r=i$$$ and $$$last_i$$$ = the index of the last number in $$$v$$$ that corresponds to a pair $$$(l, r)$$$ where $$$a_l=a_r=i$$$.
Now, in order to answer a query $$$(l, r)$$$, we must find the number of values in $$$v$$$ between $$$start_l$$$ and $$$last_r$$$ that are greater than or equal to $$$l$$$. This can be done using a merge sort tree in $$$O(log^2\ n)$$$, and the final complexity is $$$O(n\ log\ n + q\ log^2\ n)$$$.
I'm sorry if my explanation sucked. Here is a link to my submission: https://codeforces.me/contest/1864/submission/220939560
Can someone suggest some more problems like E. I found the use of Trie to calculate the total number of turns very unintuitive.
I have another solution for problem E without tries:
Consider p/q — expected value. Let's sort an array. Taking s[i] as one of the element in the game we can calculate value added to p. We know that in sorted array going from the beginning the end-game bit (XOR == 1) is moving right. So, let's brute force a position of end-game bit from the most significant one. Consider _b as bit value of s[i]. We can easily precompute how many steps we have to do before reaching this bit or even do it greedily because common prefix of two numbers is getting bigger. As we don't want to have collisions and our left bound is going right we want to know how many numbers in [l,i) have (_b^1) value in the bit. Let's make prefix sums! pref[val][bit][i] (val — {0, 1}, bit — {0...31}) And after calculating update left bound using binary search (just make pos[val][bit] and push all required numbers positions). Time complexity — O(32*NlogN)
Submission 221065798
Can anyone help me in getting error in this submission for Problem E, it is failing on testcase 6.
I solved it using tries..
Hi, I submitted my solution to D in Java 8, it's giving TLE on testcase 8. But, when I submit the code in C++ using the same logic which I used in my Java solution, it's giving AC. Any insights on how can I pass it in Java ?
Java Solution
C++ solution
For D, Similar problem in 1D array Restaurant Customers
Problem C fails for the n=15 according to editorial the answer is 7 - 15 14 12 8 4 2 1
but the min answer is 6 ie 6 — 15 10 5 4 2 1
Then what about this??
In this problem you don't need to minimize the number of operations.
include
include<bits/stdc++.h>
include <ext/pb_ds/assoc_container.hpp> // Common file
include <ext/pb_ds/tree_policy.hpp> // Including tree_order_statistics_node_update
using namespace std;
typedef __gnu_pbds::tree<int, __gnu_pbds::null_type, less, __gnu_pbds::rb_tree_tag, __gnu_pbds::tree_order_statistics_node_update> ordered_set;
//#define int long long
using ll = long long; int MOD = 1e9+7, INF = 1e9+1;
//---------------------------------------------------------------------------------------------------------------------------// ll expo(ll a, ll b, ll mod) {ll res = 1; while (b > 0) {if (b & 1)res = (res * a) % mod; a = (a * a) % mod; b = b >> 1;} return res;} ll mminvprime(ll a, ll b) {return expo(a, b — 2, b);} ll mod_add(ll a, ll b, ll m = MOD) {a = a % m; b = b % m; return (((a + b) % m) + m) % m;} ll mod_mul(ll a, ll b, ll m = MOD) {a = a % m; b = b % m; return (((a * b) % m) + m) % m;} ll mod_sub(ll a, ll b, ll m = MOD) {a = a % m; b = b % m; return (((a — b) % m) + m) % m;} ll mod_div(ll a, ll b, ll m = MOD) {a = a % m; b = b % m; return (mod_mul(a, mminvprime(b, m), m) + m) % m;} //only for prime m //--------------------------------------------------------------------------------------------------------------------------//
int gcd(int a, int b) { while (b != 0) { int temp = b; b = a % b; a = temp; } return a; } vector findFactors(int n) { vector factors; for (int i = 1; i <= n; ++i) { if (n % i == 0) { factors.push_back(i); } } return factors; } int ceil_f(int b,int a) {return(b+a-1)/a;} void solve() { int n;
cin>>n; vector<string>v(n); for(int i=0;i<n;i++) cin>>v[i]; vector<vector<int>>l(n+1,vector<int>(n+1,0)); vector<vector<int>>r(n+1,vector<int>(n+1,0)); int cnt=0; for(int i=0;i<n;i++) { vector<int>p(n+1); p[0]=l[i][0]; for(int j=1;j<n;j++) { p[j]=p[j-1]^l[i][j]^r[i][j-1]; } for(int j=0;j<n;j++) cout<<p[j]<<" "; cout<<endl; for(int j=0;j<n;j++) { cnt+=p[j]^(v[i][j]-'0'); if(p[j]^(v[i][j]-'0')) {l[i][j]=1;r[i][j]=1;} } //updating l for(int j=0;j<n;j++) if(l[i][j]==1) l[i+1][max(j-1,0)]=1; //Updating r for(int j=0;j<n;j++) if(r[i][j]==1) r[i+1][min(n-1,j+1)]=1; } cout<<cnt<<endl;} int32_t main() { int tt; cin>>tt; while(tt--) { solve(); } } please someone help in my solution Problem D please please please please please
I have a solution of problem $$$D$$$ which exploites the properties of connection between pascal triangle and diagonal in the matrix ( sounds like you need to have heavy knowledge but no just simple observations) submission
could u please explain your approach
consider a row as an array and if I give you data on which subarrays inversion happen how do you calculate whether inversion happens in particular index / column using prefix sum?
yes I think I get that part.
The idea is to to first create markings(+1 at start of subarray and -1 after it ends) and then create a prefix array based on the marking of subarrays.
But In this problem, how do you get the markings on ith row
in a cell of a row has a count of marking +1 = the count of inverted cells in the diagonal to the right from it
My solution for problem D
Was there any trick for question B i was not able to find the pattern by myself or any suggestions??
the C is amazing for bitmask practising!
My submission for F is causing Denial Of Judgement, problem authors please take a look if possible, thanks.
https://codeforces.me/contest/1864/submission/306060520