Introduction
This blog contains well-known facts and techniques about Harmonic Numbers that are scattered all over editorials of some problems, comments, and some parts of blog posts. The place where I found most of the facts explained here is the brilliant blog by Nisiyama_Suzune about Möbius inversion. However, for the untrained eye, this blog may seem as if it's investigating something advanced and the facts explained inside will be missed. Moreover, there were some omitted proofs, so I thought it would be nice to collect all these facts/techniques in one place and add their proofs in (hopefully) an understandable but precise style, which would be useful for many.
For starters, the $$$n$$$th harmonic number, $$$H_n$$$, is the sequence $$$\displaystyle H_n = \sum_{i = 1}^{n}\frac{1}{i}$$$. We will investigate two techniques related to this sequence.
1. Upper bound for Harmonic Numbers
We begin by discussing the famous upper bound for Harmonic Numbers:
This can be noted by observing the graph of $$$f(x) = \frac{1}{x}$$$ and drawing rectangles of base length 1 and height $$$\frac{1}{i}$$$ to get areas that sum up to $$$H_n$$$, similar to this (the image is taken from Stewart Calculus):
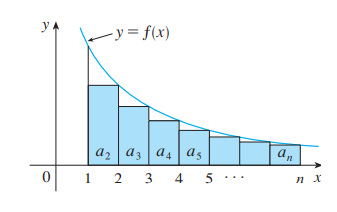
and so we have
(there is a known approximation using Euler-Mascheroni constant but I like this more simple proof).
This is why a loop like this:
for (int i = 1; i <= n; i++)
for (int j = i; j <= n; j += i) {
// some constant code
}
works in $$$O(n \log n)$$$, because $$$j$$$ iterates over all multiples of $$$i$$$ that are at most $$$n$$$, and there are $$$\displaystyle\left\lfloor \frac{n}{i} \right\rfloor$$$ such multiples, and so the complexity is just $$$\displaystyle\sum_{i = 1}^{n} \left\lfloor \frac{n}{i} \right\rfloor \le \sum_{i = 1}^{n} \frac{n}{i} = n H_n \in O(n \log n)$$$.
This is very useful whenever you want to brute force all divisors of numbers in a range $$$[1, N]$$$. This can be used to precompute the number, sum, product of divisors of all numbers in $$$[1, 10^6]$$$. You can even precompute the divisors themselves:
for (int i = 1; i <= n; i++)
for (int j = i; j <= n; j += i) divs[j].push_back(i);
This can also be used to calculate the Euler-Totient function $$$\varphi(n)$$$ and can be used in some inclusion-exclusion DP to precalculate the array $$$\text{dp}[x] = \sum_{i < j} [\gcd(a_i, a_j) = x]$$$ where $$$a_1, a_2, \dots, a_n$$$ is an array with $$$1 \le a_i \le 10^6$$$.
Example problems: (feel free to add more in the comments)
2. Distinct values of $$$\left\lfloor\frac{n}{i}\right\rfloor$$$
Now, let's get to even more interesting facts:
We will discuss why this is true and how to retrieve the exact values over the exact ranges in $$$O(\sqrt{n})$$$.
Now, note that these values are non-increasing as $$$i$$$ increases. For example, for $$$n = 10$$$, we get the values (starting from $$$i = 1$$$) $$$10, 5, 3, 2, 2, 1, 1, 1, 1, 1, 0, 0, \dots$$$. So, to find these values, we will prove the following fact:
(note that I will write a mathematical proof and it may not seem intuitive to see, and I will explain its intricacies afterwards, so don't get shocked :D)
Now, what this proof is trying to say (skip these two paragraphs if you understand and can imagine the proof) is that if you get that $$$\displaystyle \left\lfloor \frac{n}{i} \right\rfloor = q$$$ for some $$$i$$$ and $$$q$$$, and again $$$\displaystyle \left\lfloor \frac{n}{i + 1} \right\rfloor = q$$$ as well, then we know for sure that $$$n \text{ mod } (i + 1) = (n \text{ mod } i) - q$$$ by the division algorithm. (If $$$n = qi + r = q(i + 1) + r'$$$ then $$$r' = r - q$$$).
This means that with every step forward, the remainder decreases by exactly the value of the floor division. So, the remainder is maximal at the first time we reach some value $$$q$$$ (at $$$l$$$), and the remainder keeps decreasing by $$$q$$$ until we can't decrease anymore (decreasing will makes the remainder negative), and so the floor division value becomes $$$q - 1$$$ instead. So, to find the maximum point at which the floor value stays the same $$$q$$$, we find the maximum $$$k$$$ such that $$$qk \le n \text{ mod } l$$$, which is $$$\left\lfloor \frac{n \text{ mod } l}{q} \right\rfloor$$$, and we add that value to $$$l$$$ to get the same conclusion.
This fact is very useful in optimizing solutions to many problems, and I will demonstrate this by solving one example: CSES — Sum of Divisors. (The reader is encouraged to solve this on his/her own before reading on).
The problem wants to find the summation of divisors of all integers up to $$$n$$$, but with $$$n \le 10^{12}$$$. This means that at most $$$O(\sqrt{n})$$$ complexity is required. Now, the idea here is to fix a divisor and count how many times it will be a divisor. Well, for a divisor $$$d$$$, the number of multiples of $$$d$$$ up to $$$n$$$ is $$$\displaystyle \left\lfloor \frac{n}{d} \right\rfloor$$$, so the answer is just
Here, to optimize, we can fix the value of $$$\displaystyle \left\lfloor \frac{n}{d} \right\rfloor$$$ and sum all $$$d$$$ that has this value. But from what we've arrived at from the above claim, we can easily do this:
The code iterates over ranges that have the same value of floor division when $$$n$$$ is divided by them and multiplies the floor division value by the sum of elements in the range, modulo $$$10^9 + 7$$$. Each time we calculate $$$r$$$ (as defined in Fact 3) and at the end of the iteration, we make the next $$$l$$$ as $$$r + 1$$$, since $$$r$$$ is the maximum then $$$r + 1$$$ will get a new floor division value. So, the idea is always to get the ranges of the same floor value and process them however you like
for (ll l = 1, r = 1; (n/l); l = r + 1) {
r = (n/(n/l));
// q = (n/l), process the range [l, r]
}
This fact also turns out to be useful in optimizing some Möbius inversion formulas.
Example problems: (feel free to add more in the comments)










Excellent blog! I really liked the mathematical rigour of your proofs. Just a few corrections — In the first part of the blog, the code under 'Code for precomputing dp[x]' should have $$$i$$$ going from $$$N-1$$$ to $$$1$$$. Also, it will be better if you use long long to store the values of dp as many beginners make the mistake of overflow. The formula for the given dp also has a slight correction. It should be:
Thanks for the great feedback!
I read this in Gus's voice, lmfao.
There are problems, in which you need to compute $$$H_n$$$ with a certain precision. For example, PE #825. Of course,
is well-known, but sometimes it's not precise enough, so we need full expansion. Wikipedia suggests that it's
where $$$B_k$$$ are the Bernoulli numbers. I wonder what's the easiest way to derive it... Apparently, the most general case follows from Euler-MacLaurin formula, which also gives asymptotic expansion for
I saw this blog, where attempts were made to compute exactly $$$H_n$$$ with $$$n \le 10^{12}$$$ (modulo 998244353). I think the comments there may be relevant to computing $$$H_n$$$.
Edit: on second thought, the attempts in the comments can hardly be used to calculate $$$H_n$$$ as a real number with a certain precision.
I think this is a good place to advertise section 5 of my recent blog where harmonic numbers arise in the context of Stirling transformation.
In short, we have
1. $$$H_n = s(n+1,2)/n!$$$, where $$$s(n,k)$$$ denote first-kind Stirling number.
1'. By this MSE post, we have the following recursive formula for first-kind Stirling numbers involving generalised harmonic numbers:
2. Average number of cycles in a random permutation is $$$H_n$$$.
3. Harmonic numbers have a very nice OGF, namely $$$-\log(1-x)/(1-x)$$$.
I think that, in practice, we usually don't need much more than $$$H_n=O(\log n)$$$ (90% of cases), its relation with cycles in permutations and, sometimes, OGF.