Расскажите, как решается A, C, H?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
13:03:36
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
13:03:36
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 04:31:25 (g1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











И как кто решали G и I?
В G такое работает 1.5с на джаве на Я.Контесте. Найдем для каждой вершины ближайшие ~20 и оставим только эти ребра. Дальше запустим Крускала. Чтобы найти ближайшие точки, разобьем все на одинаковые квадраты так, чтобы в каждом квадрате в среднем было по ~6 точек. Для каждой точки рассмотрим все точки из 8 соседних, а также того квадрата, в котором она находится. Отсортируем по расстоянию, возьмем первые 20.
В I вроде бы все просто: при больших k ответ N, иначе узнаем вероятность того, что первый предмет будет потроган ровно k раз через Х ходов (динамикой, для X < MAGIC). Дальше для каждого Х ответ по линейности матожидиния что-то вроде N*(1-(1-p)^X).
В I можно было формулу вывести:
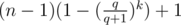 , где q = 1 - p.
, где q = 1 - p.
Чтобы вывести, переберем номер раунда, на котором все закончится и просуммируем матожидания.
В G можно написать алгоритм Прима со следующими оптимизациями:
Если в таком решении поиграться с BOUND то можно получить WA, TL на тестах в районе 25-30. Однако, при локальном тестировании оказывается, что если выбрать BOUND >= 1000, то алгоритм почти всегда находит правильный ответ. При этом, происходит порядка 5 миллионов добавлений в set и порядка 50 миллионов подсчета расстояний между парой точек.
Теперь улучшим приведенный алгоритм — на очередной итерации будем считать расстояние только до тех точек из интервала [v — BOUND, v + BOUND], для которых abs(p[i].y — p[v].y) <= LIMIT. Здесь под p[index].y обозначаем y-координату точки под номером index в отсортированном массиве. Такое отсечение позволяет существенно сократить количество подсчетов расстояний между парами точек, а также где-то в два раза уменьшает количество обращений в set и уже проходит. При этом следует отметить, что такое решение будет давать неправильный ответ, если точек слишком мало, но при n >= 10000 уже все в порядке (для маленьких n можно просматривать все точки в интервале [v — BOUND, v + BOUND]).
Мое решение получило ОК при BOUND = LIMIT = 1000.
как F?
Ответ на задачу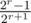 , где r — ранг матрицы. При больших значениях r ответ быстро стремится к 1/2, поэтому не нужно делать Гаусса до конца.
, где r — ранг матрицы. При больших значениях r ответ быстро стремится к 1/2, поэтому не нужно делать Гаусса до конца.
Can you please explain why such formula is correct?
Consider Ax. If it is not zero, than probability of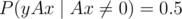 So answer equal P(Ax ≠ 0) / 2. Ax is linear combination of columns of A with coefficients from x. Consider r linear independent columns of A and corresponding coefficients from xi1, ..., xir: for every values of all other coefficients from x there are only one set coefficients xi1, ..., xir turning Ax to zero. So P(Ax ≠ 0) = 1 - 2 - r
So answer equal P(Ax ≠ 0) / 2. Ax is linear combination of columns of A with coefficients from x. Consider r linear independent columns of A and corresponding coefficients from xi1, ..., xir: for every values of all other coefficients from x there are only one set coefficients xi1, ..., xir turning Ax to zero. So P(Ax ≠ 0) = 1 - 2 - r
И про E расскажите, пожалуйста, кто как решил.
Do BFS from a random start cell, fill n/2 cells, then count the number of border cells (unvisited cells that have a visited neighbor, i.e. we have to remove the border cells in order to disconnect the region of visited cells from the rest). If the number of border cells is good ( <= 3/2sqrt(n)), done, if not, take another random starting cell and repeat.
блин, это первое что пришло в голову, неужели это ас...
Instead of random starting cell we used the leftmost cell. I don't know if it's correct, but we got an AC.
Другой подход — будем пилить фигуру пополам прямой случайного направления. Рассмотрим положение прямой, которое проходит через n/2-ую точку в порядке заметания, после этого надо непосредственно "распилить" рёбра, пересекающие нашу прямую. Для этого выкинем все левые и верхние, например, концы этих рёбер. Если их не больше чем сколько там надо, победа. Получается проверка одной прямой ровно за O(N).
100 случайных прямых хватает.
Разобъем всю фигуру на полосочки с одинаковым x. Будем вырезать только полосочки целиком. Понятно, что если мы удалим все клетки с фиксированной координатой x, то весь граф разобъется на части. Для начала попробуем вырезать только одну полоску. Если не получилось (то есть нужно вырезать слишком много клеток), напишем динамику по полоскам — сколько минимум клеток нужно вырезать, чтобы не было подряд идущих связных кусков содержащих более чем n/2 клеток.
После этого проделаем то же самое, но будем удалять полоски с фиксированным y.
В С заметим, что каждая операция первого типа либо сливает 2 цикла в один, либо разбивает один цикл на 2. Также заметим, что только операциями первого типа мы можем цикл длины K собрать за K — 1 операцию. По сравнению с использованием операций второго типа мы экономим 1 ход. Можно показать, что в таком случае нам никогда не выгодно сливать 2 цикла в 1, а также если мы уже трогаем какой-то цикл операцией первого типа, то должны разбить его до конца, причем на каждом ходу обязательно будем разбивать один цикл на 2.
Получаем следующее решение: выделим все циклы и оставим только такие, которые занимают последовательный отрезок в нашей перестановке. Для каждого такого цикла проверим, можем ли мы его полностью разобрать операциями первого типа. Все циклы, которые либо не лежат подряд, либо мы их не можем разобрать операциями первого типа, разбираем операциями второго типа.
Осталось научиться проверять, можем ли мы разобрать один цикл операциями первого типа. Для этого идем слева направо и смотрим, верно ли, что после того как мы поменяем элементы i и i + 1 местами, выйдет так, что все элементы от 1-го до i-го будут меньше всех элементов от i + 1 до конца. Если верно, то меняем местами i и i + 1 местами, после чего берем последнюю группу элементов, которая еще не разобрана и заканчивается в i и разбираем "с конца" (она обязательно должна иметь вид {a + 1, ..., a + k, a}). Сложность решения O(N).
А: захотим сделать так, чтобы из из любой ячейки памяти достигалась любая другая. По сути это найти гамильтонов цикл, но на самом деле это цикл де Бруина он ищется нахождением эйлерова пути в графе. Так мы найдём из какого состояние по какому ребру надо идти выводим это. Внезапно это работает. (Ну наверно оно должно работать так как вся память обходится)
На самом деле хватает достаточно большого цикла, к которому из остальных сходится. Мы рандомом построили цикл из порядка 37к вершин
Gassa говорил, что не любой большой цикл подходит, например 2 из 6 порядка обхода рёбер в построении цикла дают WA.
Значит нам повезло. Yay!
Мы построили цикл из 3000 вершин, сошлось.
Почему из того, что любая ячейка памяти посещается, следует, что робот посещает все клетки поля?
И как сделан чекер к задаче, кстати? Не за 3^20 же?
Я себе это объясняю тем, что мы построили так "достаточно случайное" блуждание длины почти 60к. Поле 20х20 уж должны успеть обойти. Но доказательства нет. Да и сама формулировка вопроса не совсем точная. Неправда, что любой такой цикл годится, верно что случайный из таких годится с большой вероятностью. Доказывать это никто не умеет, просто такой факт, который нужно было придумать.
Чекер мы писали, чтобы проверять свое решение, у нас было за 3^10*n*m*4 (состояние памяти, где стоим, в какую сторону смотрим) + (число циклов в этом графе)*n*m. В этом графе из каждой вершины исходит ровно одно ребро, т.е. нужно выделить циклы, к которым все сходится, и проверить, что в каждом из них есть все клетки доски.
Общие соображения о решении — от того, чего хочется, до того, что есть.
Пусть мы научились делать случайное блуждание. Тогда, чем дольше мы его делаем, тем больше вероятность посетить все клетки.
Пусть наше случайное блуждание — бесконечное, но периодическое. Тогда мы просто повторяем одну и ту же траекторию со сдвигом.
Значит, в нашем случайном блуждании основной критерий качества — длина периода: чем она больше, тем лучше.
В идеале замкнём в один период все 59 049 внутренних состояний робота, то есть построим цикл де Браана. Можно также просто построить просто какой-то длинный цикл, в который мы рано или поздно придём из любого другого состояния, как в решении Petr Team.
Важно построить именно случайное блуждание: слишком регулярное движение посетит меньше клеток. Например, если строить эйлеров цикл с фиксированным порядком рёбер
f,l,rиз вершины, не любой из шести возможных порядков подходит. С другой стороны, решение, которое выбирает порядок случайно в каждой вершине, при >400 запусках с разным randseed отработало правильно во всех случаях. То есть, если вы в решении не используете случайность, она сама может случиться с вами в виде Wrong Answer.Как работает проверка.
Есть множество внешних состояний робота S: тройки (x, y, d), их 20 × 20 × 4 = 1600.
Есть множество внутренних состояний робота T: — история из 10 команд, их 310 = 59 049.
Рассмотрим граф, вершины которого — элементы S × T. Всего вершин в графе 1600·59 049 = 94 478 400, меньше ста миллионов.
Из каждой вершины выходит ровно одно ребро, зависящее и от внутреннего состояния (что мы пытаемся сделать), и от внешнего (не упёрлись ли мы при этом в стенку).
Значит, этот граф состоит из циклов, в которые ведут хвостики. Хвостик добавляет посещённые состояния к нашему пути, а значит, разве что добавляет посещённые клетки. Значит, худший случай — хождение по циклу без хвостиков.
Важно, что цикл в нашем графе можно начать рассматривать из любого места, так как рёбра-переходы уже учитывают то, что мы иногда утыкаемся в стенки.
Будем искать циклы в этом графе. Начнём из произвольной вершины и будем отмечать посещённые вершины. Если мы пришли в вершину, посещённую в более ранних поисках, мы уже рассмотрели соответствующий цикл, просто в предыдущий раз пришли в него по другому (возможно, пустому) хвостику.
Если же мы нашли вершину, посещённую в этом же поиске — запустим из неё поиск ещё раз, уже точно зная, что она лежит на цикле, и отмечая по ходу клетки, которые мы посетили (это часть внешнего состояния в каждой вершине). Найдя нашу вершину в третий раз, проверим, что мы за время обхода цикла посетили все клетки.
В процессе поиска каждая вершина может находиться в одном из небольшого количества состояний. На одну вершину вполне хватает диапазона значений одного байта.
Из соображений симметрии работу можно сократить в несколько раз. На тесте 20 × 20 и правильном ответе чекер работает меньше секунды и делает примерно 90 000 000 переходов.
Где можно найти официальный разбор авторов? =)
Узнать у авторов в личном порядке, никаких официальных разборов нет ;)
Кто авторы? =)
Подписано снизу каждой страницы с условием задачи =)
Where can I get the problems? What about testing them? =)
(BTW Sorry I'm not good at Russian)
You can get the russian version of problem statements here and english version here.
Speaking about upsolving or solving opencup contest you can read this thread. Perhaps, it will be helpful.