Хеширование корневых деревьев

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Я обнаружил небольшую нехватку материалов на эту тему и хочу начать со статьи rationalex:

Задача

Хотим научиться сравнивать корневые деревья на изоморфизм (равенство с точностью до перенумерования вершин + корень одного дерева обязательно переходит в корень другого дерева).

Хеш вершины

Заметим, что поскольку мы не можем апеллировать к номерам вершин, единственная информация, которую мы можем оперировать — это структура нашего дерева.

Положим тогда хешем вершины без детей какую-нибудь константу (например, 179), а для вершины с детьми положим в качестве хеша некоторую функцию от отсортированного (поскольку мы не знаем истинного порядка, в котором дети должны идти, нужно привести их к одинаковому виду) списка хешей детей. Хешом корневого дерева будем считать хеш корня.

По построению, у изоморфных корневых деревьев хеши совпадают (доказательство индукцией по числу уровней в дереве автор оставляет читателю в качестве упражнения).

Полиномиальный хеш не подходит

Рассмотрим 2 дерева:

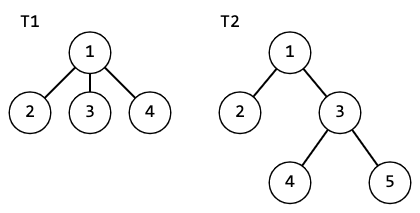
Если мы посчитаем для них в качестве функции от детей взять полиномиальный хеш, то получим: $$$h(T1)=179+179p+179p^2=179+p(179+179p)=h(T2)$$$

Какую же хеш-функцию взять?

В качестве хорошей хеш-функции подойдёт, например

$$$h(v)=42 + \sum_{u \in sorted\_by\_hash(child(v))} \log(h(u))$$$

Для этой хеш-функции может показаться, что можно не сортировать хеши детей, однако это не так, потому что при вычислении чисел с плавающей точкой у нас возникает погрешность, и чтобы это результат суммирования был одинаковый для изоморфных деревьев, суммировать детей надо тоже в одинаковом порядке.

Пример более complicated хеш-функции:

$$$h(v)= \big[\sum_{u \in sorted\_by\_hash(child(v))} h(u)^2+h(u)p^i+42\big]\mod2^{64}$$$

Асимптотика

Всё что нам нужно делать на каждом уровне — это сортировка вершин по значению хеша и суммирование, так что итоговая сложность: $$$O(|V| \log(|V|))$$$

Хочу продолжить от себя:

В реалиях Codeforces у данных подходов есть проблемы в виде взломов (что можно увидеть, например, по взломам этой задачи). Поэтому хочу рассказать о подходе, при котором не возникает коллизий.

Что же за хеш-функция?

Давайте для вершины отсортируем хеш-функции детей и сопоставим этому массиву номер, который и будем считать хешем вершины (если массив новый, то присвоим ему минимальный незанятый номер, иначе возьмём тот который уже дали).

Почему это работает быстро?

Легко заметить, что суммарный размер массивов, которые мы посчитали, равен $$$n - 1$$$ (каждое добавление это переход по ребру). Благодаря этому, даже используя для сопоставления treemap, на все обращения к нему потребуется суммарно $$$O(n \cdot \log(n))$$$. Сравнение ключа размера $$$sz$$$ с другим ключом работает за $$$O(sz)$$$ и таких сравнений для каждого ключа произойдёт $$$O(\log(n))$$$, а сумма всех $$$sz$$$ как мы помним равна $$$n-1$$$, так что получается суммарно $$$O(n \cdot \log(n))$$$. (Вы могли подумать что стоит использовать hashmap, но это не улучшает асимптотику и вызывает вероятность коллизии).

Комментарии (37)

Показать архивные | Написать комментарий?

EzikBro

21 месяц назад, # |

Это же просто копия статьи с алгоритмики? Хотя бы ссылку вставь в статью: https://ru.algorithmica.org/cs/hashing/isomorphism/#%d0%ba%d0%be%d1%80%d0%bd%d0%b5%d0%b2%d1%8b%d0%b5-%d0%b4%d0%b5%d1%80%d0%b5%d0%b2%d1%8c%d1%8f

→ Ответить

Vladosiya

21 месяц назад, # ^ |

← Rev. 2 →

Статья в основном скопирована, с разрешения Александра Гришутина (который упомянут в блоге и писал её для алгоритмики). От себя докинул только последний способ и перевод на английский, на котором не обнаружил подобных тем.

Golovanov399

← Rev. 3 →

+25

First of all, what do you call a "polynomial hash"? Is it something like sum of "take $$$i$$$-th child, multiply its hash by $$$p^i$$$"? If it is true, then this "hash" changes when we swap two children with different hashes, which shouldn't happen.

UPD: okay, I wasn't very observant and didn't read the whole paragraph with "hash of subtree is hash of sorted list of smth"

Second, I think that the last way you mentioned is the most popular and simple, but just out of theoretical interest one can read this ancient article by rng_58. It contains two pictures which seem to have expired, but I have the second of them:

the relevant pic

sakib.safwan

+11

I tried the approach mentioned in the rng_r8's blog (Multivariable polynomial hashing) but got wa on test case 7. Did I implement it in the wrong way or did the main case had the hack input for which it would give wa.

submission link

people_plus_plus

20 месяцев назад, # ^ |

You did something wrong. My solution got AC

Thanks people_plus_plus

I compared my code with yours and changed two things and it got accepted.

Firstly, for all vertex my code did....

hash[vertex] *= (depth[vertex] + hash[child]), but I didn't mutliply the hash of that vertex with its own depth. (I didn't multiply the hash of parent which of course was 0 during that time).

It still gave wa.

Then I used mod in the hash multiplication instead of just purely using unsigned long long which automatically mods any value greater than unsigned long long max with unsigned long long max.

However, In rng's blog, he didn't tell to multiply the hash with depth of that vertex itself.

Also, it would be really helpful if you can tell me what is the reason that using a smaller MOD (1e9 + 9) instead of a larged MOD (unsigned long long) avoided collision. Should I do that every time I use hashing?

Where is a reason why you should not use auto mod like you did in your first submission. Standart types use mod $$$2^x$$$ and it can be easily get collision even on small data! You can read about this here https://codeforces.me/blog/entry/4898?locale=ru

In simple words: dount use automatically mods, use your own mods like $$$10^9 + 7$$$. To be sure, use int64 mods. Be carefull when you use hash on codeforces, because there are hacks. You can avoid being hacked by choose a random prime-mod number.

Formatci

-150

Did you take any permission to publish my algorithm?

chenshi028

+31

There's a way to hash rooted trees which has a better time complexity and is also easy to implement, whose expected number of collisions doesn't exceed $$$O(\frac{n^2}{2^w})$$$. It is mentioned here.

To avoid being hacked, you can use random parameter instead of 1237123 in the article when solving Codeforces problems.

micho

Can you explain the proof of the expected number of collisions and the meaning of $$$w$$$ in $$$2^w$$$? Thank you.

dmkz

+32

Рекомендую также лекцию по изоморфизму деревьев от Сергея Копелиовича в сборнике с лекциями и разборами «Зимняя школа по программированию 2013», страница 264. Там есть крутые задачи, крутые хеш-функции и крутые идеи.

Деды узнавали об изоморфизме деревьев по этой лекции. Также там есть изоморфизм некорневых (неподвешенных) деревьев.

UPD. Пользуясь случаем рекомендую также раритетную лекцию по жадным алгоритмам в том же сборнике от того же автора чуть ниже, а ещё фулл контест по Warcraft 3 в сборнике за другой год (не помню год).

lemelisk

Там ещё описан способ докрутить метод с классами эквивалентности, описанный в конце блога, до $$$\mathcal{O}(n)$$$ (без логарифма). Если у кого-то с английским получше, чем у меня, можно его перевести.

Polynomial hash works fine, you just need to represent tree's euler tour as a correct bracket sequence — ( when you walk along an edge from parent to child and ) when you go backward from child to parent. So T1 will be ()()() and T2 will be ()(()()). Then hash it as usual string (of course, with sorting childs' hashes).

Doesn't it look like it's easier to create a collision with such hashing? (In context of hacks)

Every tree is just a string in such representation. If we use polynomial hashing for strings, why shouldn't we use it in this case?

Honeynutz

I solved https://codeforces.me/contest/1800/problem/G using your idea. It's nice

AndreyPavlov

Прикольно

Я сдал то же самое на контесте, что вы описали в своём комментарии. Ходят слухи, что этот детерминированный способ рассказывают на воркшопах МФТИ.

Доказательство упирается в асимптотику вставки и поиска $$$N$$$ векторов в мапе суммарной длины $$$N-1$$$? Может асимптотика будет такая же как просто сортировка набора из $$$N$$$ векторов суммарной длины $$$N-1$$$?

UPD. Увидел, что вы удалили свой коммент из-за того, что данный способ описан в самом конце блога, и доказательство к нему тоже.

teraqqq

ЧЕРТ ТОЖЕ САМОЕ НАПИСАНО В СТАТЬЕ А МНЕ БЫЛО ЛЕНЬ ЧИТАТЬ

sahaun

Can anybody suggest some problems on the topic?

UPD:

1800G - Симмеtreeя

763D - Тимофей и плоское дерево

Kattis — Two Charts Become One

Noble_Mushtak

I recently solved a problem from an ICPC regionals using this technique: Two Charts Become One

MikeMirzayanov

+111

It seems often a good idea to compute not hashes for subtrees, but simply numeric representations $$$val(u)$$$ — consecutive integers from $$$0$$$ and beyond, where $$$u$$$ is the root, which defines a subtree rooted at $$$u$$$. The values $$$val(u)$$$ and $$$val(v)$$$ will be equal if and only if the subtrees with roots $$$u$$$ and $$$v$$$ are equal (or isomorphic).

You can just use map<vector<int>, int> vals for memoization. Then if for $$$u$$$ you need to calculate the value of $$$val(u)$$$, then take all children $$$w_1, w_2, \dots, w_k$$$ of $$$u$$$ and make a vector $$$[val(w_1), val(w_2), \dots, val(w_k)]$$$. If it has a value in $$$vals$$$, then take the value from there, if not, enter the next integer (well, just use current $$$vals.size()$$$).

And just recursively calculate this for all subtrees. In total, it will work for $$$O(nlogn)$$$, apparently. And no issues with possible hash collisions. You can think of the resulting values as perfect hashes.

why_I

Thank you! i literally do not know about hashing at all. i just saw your comment and solved the problem 1800G - Симмеtreeя .

My submission if anyone want :- 195934874

aayushgupta023

Hey, may you please explain a little more on how this algorithm works? I am not able to understand... Please!

aqheev

+18

Here's how I understand it, and hopefully it helps you.

We want to assign a number for every node $$$u$$$ (we write this as $$$val(u)$$$) based on the structure of its children (by looking at $$$childrenInfo(u) = [val(w_1), val(w_2), ..., val(w_k)]$$$ where $$$w_1, w_2, \dots, w_k$$$ are children of $$$u$$$). So, two nodes with the same $$$childrenInfo$$$ will have the same value in $$$val$$$ and have the same subtree structure (or isomorphic). For example, in this tree:

tree example

Nodes $$$4$$$, $$$5$$$, $$$6$$$, $$$9$$$, and $$$12$$$ have no children (so each $$$childrenInfo$$$ is $$$[$$$ $$$]$$$), so we assign $$$val(4)$$$, $$$val(5)$$$, $$$val(6)$$$, $$$val(9)$$$, and $$$val(12)$$$ the same number, say 0.
Nodes $$$3$$$, $$$8$$$, and $$$11$$$ have the same children info, since $$$childrenInfo(3) = [val(5)] = [0]$$$, $$$childrenInfo(8) = [val(9)] = [0]$$$, and $$$childrenInfo(11) = [val(12)] = [0]$$$. That means we assign $$$val(3)$$$, $$$val(8)$$$, and $$$val(12)$$$ the same number but different from the previous one, say 1.
Nodes $$$2$$$ and $$$7$$$ have the same children info, since $$$childrenInfo(2) = [val(4), val(3)] = [0,1]$$$ and $$$childrenInfo(7) = [val(8), val(6)] = [1,0]$$$. Note that the order of children does not matter in $$$childrenInfo$$$, so $$$[0,1]$$$ and $$$[1,0]$$$ are the same (we can sort them first before comparing). So we assign $$$val(2)$$$ and $$$val(7)$$$ the same number, say 2.
Node $$$10$$$ has $$$childrenInfo(10) = [val(11)] = [1]$$$. Let's assign $$$val(10) = 3$$$.
Node $$$1$$$ has $$$childrenInfo(1) = [val(2), val(7), val(10)] = [2,2,3]$$$. Let's assign $$$val(1) = 4$$$.

The algorithm works like DFS. So to calculate for $$$val(u)$$$, we want to first get $$$childrenInfo(u)$$$. Notice that to get $$$childrenInfo(u)$$$, we have to know $$$val(w_i)$$$ for all of its children $$$w_i$$$ first. So do the DFS like the following code snippet. Note that we use vals to store/remember what number to assign to $$$val(node)$$$ with certain $$$childrenInfo$$$.

Code

vector<int> val(n, -1);
map<vector<int>, int> vals;

void dfs(int node, int parent) {
  // we run DFS for all child first (so that val for children is calculated),
  // then we add the val of the child to childrenInfo after.
  vector<int> childrenInfo;
  for (int child : adj[node]) {
    if (child != parent) {
      dfs(child, node);
      childrenInfo.push_back(val[child]);
    }
  }
  sort(childrenInfo.begin(), childrenInfo.end());

  if (vals.count(childrenInfo) == 0) {
    // if it is the first time we encounter a node with
    // this childrenInfo, then we assign it a new number (like vals.size()).
    vals[childrenInfo] = vals.size();
  }
  val[node] = vals[childrenInfo];
}

// then run dfs(root, -1)