Обратите внимание на бонусы в некоторых задачах, и если вы умеете их решать, пожалуйста, напишите об этом в комментариях.
В задаче нужно было найти время ожидания для каждой очереди, просуммировав покупки по всем людям, и найти минимум.
В задаче нужно было найти максимально длинную гирлянду, которую можно составить из тех элементов, что у нас есть.
Во-первых, если какой-то цвет нужен, но его нет, то ответ — -1.
Иначе, ответ всегда существует, и является целым числом.
Просуммируем ответы по всем цветам по отдельности.
Пусть у нас есть a кусков бумаги некоторого цвета, а нужно — b. Тогда если a > = b, то к ответу можно прибавить b — повесить b кусков по одному метру, а если a < b, то к ответу можно прибавить a, использовав все куски, что есть в наличии. Итого, каждый цвет дает к ответу min(a, b).
В задаче требовалось расположить прямоугольный треугольник с катетами a, b на плоскости с вершинами в целых точках.
Если искомое расположение существует, то катет a всегда можно представить как вектор с целыми координатами A{x;y}, при чем a2 = x2 + y2. Переберем все возможные x (1 ≤ x ≤ a - 1), проверим, что y получается целым числом.
Вектор, перпендикулярный вектору {x;y} — { - y;x}. Возьмем вектор B{ - y / g;x / g}, где g = gcd(x, y). Треугольник можно уложить на плоскость лишь тогда, когда b делится нацело на |B|, где |B| — длина вектора B. Кандидат на ответ — треугольник (0;0)(x;y)( - y / g * b / |B|;x / g * b / |B|), нужно лишь не забыть проверку на то, что гипотенуза не параллельна осям координат.
Сложность решения — O(n).
В задаче требовалось промоделировать путь персонажа по графу.
Заметим, что если мы пришли в вершину i, то ребра во всех вершинах с номерами меньшими, чем i, повернуты в pi. Это дает нам возможность заметить рекуррентную формулу: пусть dpi — число шагов, необходимое, чтобы добраться из вершины 1 в вершину i, если все ребра изначально повернуты назад, в pi. тогда dpi + 1 = 2dpi + 2 - dppi. Ответом будет dpn + 1.
Сложность решения — O(n).
BONUS: Умеете ли вы решать задачу, если нет ограничения, что pi ≤ i? В такой формулировке задача становится более интересной, но я пока не знаю решения.
В задаче требовалось научиться прибавлять в оффлайне на отрезке числа сочетаний.
Будем смотреть, как изменяется задача при увеличении k от малых чисел к большим.
1) Все запросы имеют K = 0
Прибавляется каждый раз единица на отрезке.
Для решения задачи нужно прибавить на некотором массиве b[] в ячейку b[L] единицу, вычесть из b[R + 1] единицу, а после выполнения всех операций построить массив a как массив сумм на префиксах массива b.
2) Все запросы имеют K = 1
Прибавляется арифметическая прогрессия 1 2 3 4 ...
Для решения задачи нужно прибавить на некотором массиве c[] в ячейку c[L] единицу, вычесть из с[R + 1] единицу. После выполнения всех операций можно построить массив b как массив сумм на префиксах массива c. В таком массиве мы на каждом отрезке прибавили единицу. Если после этого для каждого запроса вычесть из b[R + 1] число C(R — L + 1, 1) = (R — L + 1), и построить массив а как массив префиксных сумм над массивом b, несложно увидеть, что массив а будет ответом.
3) Все запросы имеют произвольное k
Пускай у нас есть массив a[N][K].
обобщая предыдущие случаи, можно понять, что если поступает запрос L, R, K, нужно сделать операции
a[L][K + 1] += 1
a[R + 1][j] -= C(k + 1 — j + r — l, k + 1 — j) для всех 1 <= j <= K + 1
после чего построить необходимые суммы на префиксах для всех значений K спускаясь от больших K к меньшим.
Доказать, что нужно отнимать именно такое число сочетаний, проще всего, если посмотреть, как расположены эти числа в треугольнике Паскаля — легко увидеть, что это число является суммой всего ряда чисел перед ним.
Сложность решения — O((n + m)k).
407D - Наибольшая подматрица 3
В задаче требовалось найти наибольшую по площади подматрицу, состоящую из различных чисел.
Будем идти от медленных решений к более быстрым.
1) Решение за O(n6): Перебираем две противоположные вершины прямоугольника-ответа и проверяем, что все числа внутри различны.
2) Решение за O(n4): Фиксируем верхнюю и нижнюю границы прямоугольника-ответа (O(n2)).
Используем метод двух указателей при переборе левой и правой границы: пока в прямоугольнике нет одинаковых чисел, двигаем правую границу, пока есть — двигаем левую границу. Проверка при сдвиге границы — O(n), сдвигов — O(n).
3) Решение за O(n3logn): Введем функцию maxR(Left): наибольшее значение Right, такое, что при фиксированных Up и Down в прямоугольнике (Up, Down, Left, Right) нет одинаковых чисел. Заметим, что для всех i выполняется maxR(i) <= maxR(i + 1).
Как изменяются значения этой функции при сдвиге Down вниз? Каждое значение maxR(Left) может либо остаться таким же (если отрезок(Down, Down, Left, maxR(Left)) добавил лишь новые числа), либо уменьшиться.
Когда maxR(Left) уменьшается? Лишь тогда, когда одно из чисел с только что добавленного отрезка уже было в прямоугольнике.
Сдвигая Down вниз рассмотрим все числа в ряду Down. Для каждого числа в столбце j найдем индексы i и k такие, что i <= j, в столбце j есть вхождение числа a[Down][j] между строками Up и Down-1, i — максимально; k >= j, в столбце k есть вхождение числа a[Down][j] между строками Up и Down-1, k — минимально. Найдя такие индексы i и k (для этого удобно использовать set, для каждого цвета храня столбцы, где он встречался на данный момент между строками Up и Down), можно обновить maxR[i] = j — 1, maxR[j] = k — 1. Этого будет достаточно. Несложно заметить, что после описанных действий, если мы прокинем по всем i = m..1 maxR[i] = min(maxR[i], maxR[i + 1]), то мы вновь будем иметь корректные значения функции maxR(Left), и можно пересчитать ответ для данных Up и Down за O(n).
4) Решение за O(n3):
Предыдущее решение, несмотря на хорошую асимптотику, требует хранения большого количества set'ов. Это работает очень медленно даже на небольших тестах.
Избавимся от логарифма. Set используется лишь при поиске ближайших слева и справа чисел, равных данному, лежащих в строках с номерами от Up до Down. Заметим, что при сдвиге границы Up ближайший сверху элемент для данного a[i][j] отдаляется. Это наводит на мысль, что, двигая Up снизу вверх, можно заставить ближайший к a[i][j] элемент приближаться к столбцу j, и теперь, сдвигая Up вверх, мы можем, взяв число с верхнего ряда, быстро (за O(n)) определить все числа такие, что он будет для них ближайшим, и обновить для них ближайшее число.
Такое решение использует O(n2) памяти и O(n3) времени.
BONUS: Умеете ли вы решать эту задачу быстрее, чем за O(n3)? У меня не получилось, но никаких предпосылок того, что решения нет, я не нашел.
На контесте задачу, к сожалению, никто не решил, но в дорешивании первым оказался hza, с чем мы его и поздравляем.
В задаче требовалось найти наидлиннейший подотрезок, удовлетворяющий условию.
Сведем задачу к d = 1.
Если d = 0, то ответ — наидлиннейший подотрезок из равных чисел, этот случай обрабатываем отдельно.
Если d ≠ 0, то заметим, что если на некотором отрезке есть два числа ai, aj таких, что ai % d ≠ aj % d, то этот отрезок не может быть хорошим.
Разобьем исходную подпоследовательность на отрезки подряд идущих чисел, дающих равные остатки от деления на d, поделим каждое число на d, будем решать для каждого отрезка задачу отдельно, сказав, что d = 1.
Заметим, что отрезок [L, R] является хорошим тогда и только тогда, когда max(L, R) — min(L, R) — (R — L) <= k, и на отрезке с L по R нет одинаковых чисел. Объясняется это просто — если на отрезке нет повторяющихся чисел, то max(L, R) — min(L, R) — (R — L) — именно количество чисел, которые необходимо добавить, чтобы отрезок состоял из всех чисел с min(L, R) по max(L, R).
Для каждого L найдем такое maxR[L], что на отрезке с L по maxR[L] нет повторяющихся чисел, а maxR[L] — максимально. Это делается за O(nlogn) любым способом, например, проходом с map'ом.
Научимся для каждого фиксированного L поддерживать массив a[R] = max(L, R) — min(L, R) — (R — L). Если у нас есть такой массив, то для того, чтбы найти ответ, необходимо быстро найти такое наибольшее R, что a[R] <= k.
Нам потребуются два стека и дерево отрезков с операциями "Прибавить число на отрезке", "Найти минимальный элемент на отрезке" и "Найти самое правое число, такое, что оно не превышает k". Будем перебирать L справа налево (от n до 1). Как выглядит функция max(L, R) при фиксированном L? Ее значения представляют собой набор отрезков, на которых максимумом является первый элемент отрезка. (пример: для массива 6 4 8 0 7 9 функция max(1, R) будет иметь вид 6 6 8 8 8 9) Как изменяется функция при сдвиге L влево? Некоторые отрезки поглощаются новым элементом, если новый элемент больше значения на отрезке. Заметив, что все значения массива не убывают, будем хранить все такие отрезки в стеке, а при добавлении нового элемента a[L] вытаскивать отрезки из стека, пока значение на вершине меньше нового, и добавим на стек новый отрезок, который покроет L и все, что мы вытащили. Если каждую операцию со стеком сопровождать запросом "Прибавить число на отрезке", то мы уже можем получить массив a[R] = max(L, R).
Функция min(L, R) ведет себя абсолютно аналогично, и используя второй стек мы получаем a[R] = max(L, R) — min(L, R). Для того, чтобы получить член (R — L) достаточно просто каждый раз при сдвиге L влево отнимать единицу на отрезке [L, n].
Теперь запрос "Найти самое правое число, такое, что оно не превышает k". Сначала дерево отрезков разбивает отрезок запроса L..R на log(n) отрезков длиной степени двойки. Разобьем запрос на такие отрезки и выберем самый правый отрезок, минимум на котором <= k. Теперь будем спускаться по этому отрезку вниз в дереве отрезков — если в правом сыне min <= k, то в правого, иначе в левого. Так мы найдем искомый элемент.
Итак, для каждого фиксированного L делаем запрос на отрезке L..maxR(L) о самом правом числе, не превышающем k. Это один из кандидатов на ответ. Все. Раз мы делаем запрос на отрезке, на котором нет различных чисел, то любое число на этом отрезке неотрицательно, и min работает корректно.
Суммарное время работы — O(nlogn).
BONUS: Задача и сама по себе не из простых, но умеет ли кто-нибудь решать ее по методу "навороти побольше"? Интересно, как решать хотя бы на дереве.
BONUS2: Есть очень быстрое решение за O(n2). Давайте для отрезка [L; R] так же посмотрим на значение f(L, R) = max(L..R) — min(L..R) — (R — L) — K. f(L, R) можно считать для отрезка за O(1). Если f(L, R) <= 0, то отрезок — кандидат на ответ. Если f(L, R) > 0, то следующий отрезок, который стоит рассмотреть — [L; R + f(L, R)], потому что для всех r: R < r < R + f(L, R) отрезок [L; r] не будет k-d последовательностью, поскольку при добавлении одного числа в отрезок f(L, R) может либо возрасти на произвольное число, либо уменьшиться на единицу. Если так написать решение за квадрат, используя для начального R при фиксированном L значение L + curAns, то решение в среднем работает очень быстро, и получает ТЛ лишь на специальных тестов. Вполне возможно, что это решение можно оптимизациями довести до такого, что оно пройдет все тесты.











А можно добавить авторские решения?
Да, можно, скоро постараюсь добавить.
Получается циклическая реккуррентная система. Как такое решать?
Unable to understand 407A — Triangle.
Proof for this???
I can't understand this solution too. But you may use solution with O(n^2). Like my solution,
http://codeforces.me/contest/408/submission/6183126
Fixing the point (0,0) to be the vertex of the triangle that has the right angle, you need to find 2 other points. first, we find the gcd of the given 2 distances. We try to find a point in the first quadrant such that the distance from (0,0) is the gcd. If we find one, we multiply the coordinates, to get one of the required distances. Let this point be (x,y). The slope of the line joining (0,0) and (x,y) is y/x. the slope of a line perpendicular to this line is -x/y ( -1/slope of other line). now multiply (-x,y) to get the other point. Now, we have to check if the line joining the 2 points, are parallel to the x axis/ y axis. If they are, swap the distances you used to locate the first point in the first quadrant and recalculate the second point. If they are still parallel, print NO, else print the points.
To locate a integer point, simply iterate from 1, and check if (let the distance be a) a * a — i * i is a perfect square.
Please forgive me, if its not clear. Hope it helps.
why this output incorrect ?
input 5 5
my output YES 0 0 3 4 4 3
checker log says that : wrong answer incorrect triangle
it's not a right triangle
Ok. I didn't see it must be a right triangle. Thanks.
Why can you fix that (0,0) is a vertex?
Translation doesn't change a parallelity..
The inner product of (x1,y1)、(x2,y2) is zero, which means x1*x2+y1*y2=0. Thus, x2:y2=-y1:x1.
I can't understand this solution too.
There is O(n) soln for this
my solution > 13779488
Весь контест думал над тем, умею ли я такое решать :( А ты умеешь?
P. S. Задачи очень клевые!
Нет, я тоже не умею.
Рад, что понравились)
I think many people are waiting for the Tutorial of other problems!!!please!!!!!
Sorry, I am running out of time, I'll translate that part of editorial as soon as I can. If you want to see editorial right now, you can try view russian version with Google Translate.
what kind of black magic is this?!!
15ms.31ms.The time is reported witn an error of tens of miliseconds. This is well within the error margin (it's well possible that the first algorithm ran in 40 ms and the other in 0 ms).
JuanMata don't forget that there are other factors that makes O(N) requires more runtime than O(N^2) in reality , like function calls , unexpected jumps to some far locations in memory, and the data structure you use , how you manage your code , and how your code tampers the memory ...... :)
That shouldn't be it in this case. Even if the constant factor's 10 times worse, the runtime is still 100 times better on the largest inputs. What you say usually matters when comparing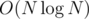 ,
, 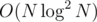 and
and 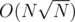 solutions, but hardly here.
solutions, but hardly here.
You could be in the same situation if you submit one source code several times.
Because there is no right triangle with such parametres.
Oh, sorry, my reply was for another comment.
??
http://codeforces.me/contest/408/problem/C http://codeforces.me/contest/408/problem/C
why does it is showing wrong answer for input : 15 20 my output: YES 0 0 9 12 -12 16
Because there is no right triangle with such parametres.
I think there's a problem with this test-problem B.garland-DIV2: input : (yqfqfp/ tttwtqq) Answer is 2,right? but Checker log says: -1. Can anybody expain why?
You dont have any 't' and 'w' and you can't make 'tttwtqq' with only 'y','q' and 'f' letters
That was really a detail that you have n SHEETS and you supposed to make m PIECES completely!!
Well ......
Can someone explain the solution to problem 407C please?
I already did
How to solve the problem 407C — Curious Array. I think it is so difficult.
I already did
And I'm posting the same comment as an answer to 2 successive ones because I have bad experience with people not reading other comments before asking...
I don't care what you do! I just express my mood! Don't brainlessly deduct! ok!!!
Someone that explains 407B better)?:)
let us assume that
dp[i]be the number of moves required to start at room i and come back to i.now when we move from room i to p[i], we would have odd number of crosses on room p[i], therefore we would need
dp[p[i]]more moves to come back to p[i] and make it have even number of crosses. so afterdp[p[i]]+1moves, we would be at position p[i] + 1.solving similarly for other rooms, we can get
dp[i] = 1 + (dp[p[i]]+1) + (dp[p[i]+1]+1) + ... + (dp[i-1]+1)(the first1is the initial move from i to p[i]).now u should be able to see that the final answer would be
(dp[1]+1) + (dp[2]+1) + (dp[3]+1) + ... + (dp[n]+1).the above solution works in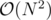 . it can be reduced to
. it can be reduced to 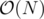 by using prefix sums.
by using prefix sums.
well with memo solution above still running in O(N)
same idea with me, sorry I have clicked the button of "I do not like it" by mistake ,
Thanks for the detailed explanation :)
suppose that you are in room
kthe 1st time (aka the number of crosses is odd), and the number in roomkisp[k].let
s[k]the steps you need to go from roomkto roomk+1.in order to do that:
you need
1step to go from roomkto roomp;you need
s[p[k]]+s[p[k]+1]+s[p[k]+2]+...+s[k-1]steps to go from roompto roomk. now the number of crosses is even;1step to go from roomkto roomk+1.so
s[k]=2+s[p[k]]+s[p[k]+1]+s[p[k]+2]+..+s[k-1]and of course
answer=s[1]+s[2]+..+s[n]with
n=1000solving time is30ms:)Can you explain the really short solution?
"In this problem you had to simulate route of character in graph. Note that if you are in vertice i, then edges in all vertices with numbers less than i are turned to pi. It gives us opportunity to see a recurrence formula: let dpi be number of steps, needed to get from vertice 1 to vertice i, if all edges are rotated back, into pi. Then dpi + 1 = 2dpi + 2 - dppi. Answer will be dpn + 1."
I don't really understand; what is a "rotated back" edge? What does it mean "numbers less than i are turned to pi"
Hello AkshajK, think of it this way.
dp[i+1] is composed of three sums.
dp[i+1] = S1 + S2 + S3
S1 := dp[i], since we need to get to point i first.
S2 := 2, one for the move back to p[i] and one for the jump from i to i+1
S3 is more interesting. Once, we've jumped back to p[i], how many jumps does it take to get back to i?
Jumps to reach (p[i]+1) := dp[p[i] + 1] — dp[ p[i] ] . Why? Because it's just the total number of moves to reach p[i] + 1 minus the number of jumps we needed originally to get to p[i] i.e dp[p[i]].
Thus S3 := (dp[p[i] +1] — dp[p[i]]) + (dp[p[i] +2] — dp[p[i]+1]) + ... (dp[i] — dp[i-1])
This reduces to, S3 := dp[i] — dp[p[i]]
Adding the three sums should give you the final answer.
I understood the solution. I had a simple doubt.
Let's say the input is:
2
2 2
In this case according to me, the answer should be 3 (1->2->2->3). He only used the portal three times, but according to the solution it'll give the answer as 4.
Am I missing something? Or is there an explanation?
Thanks!
what about pi<=i, here you have 2>1
6 days have passed and there are still no solutions to C-E. I can hardly call it soon...
Для каждого числа в столбце j найдем индексы i и k такие, что i <= j, в столбце j есть вхождение числа a[Down][j] между строками Up и Down-1, i — максимально ? По моему тут ошибка.
There are no solutions for the last 3 challenging challenges, please speedup, we are waiting for that.
Why aren't there any solutions for the last 3 problems? Do the authors forget this blog???
so many statement mistakes in this tutorial!!
Anyone solving the 'Bonus' Section of Div1 B — Long Path?
I'm trying to solve 407A — Triangle, I'm not able to understand the tutorial above. Why GCD is used? Also, how did we end up taking those points?
Can someone tell me any prereq. reading that I need to do before I'll be able to understand the concepts mentioned in tutorial above?
Thanks!!
Let point where base and perpendicular meet be {x,y}. Then we can write other two points in form of the angle which line connecting them with {x,y} make with x-axes and radial distance. Let these points be {x1,y1} and {x2,y2}. Then,
x1 = x + a*cos(theta) ; y1 = y + a*sin(theta)
x2 = x — b*sin(theta) ; y2 = y + b*cos(theta)
where theta is angle between line connecting {x,y} and {x1,y1} and horizontal axes.
Now since x, x1 are integers therefore a*cos(theta) should also be integer.
Let cos(theta) = p/q. Then q should be multiple of both a and b. Smallest such q will be lcm(a,b). Now , a*cos(theta) = a*(p/lcm(a,b)) = (p/(b/g)) = (p*g)/b which can only be integer between [-a,a] since, -1 <= cos(theta) <= 1.
Other way to optimize D:
Instead of using set use bitset of size maxn initially filled with zeros. Anytime we insert value at point i just set ith bit to 1. To find next filled element we can just use _Find_next on bitset, sadly bitset has no _Find_prev, but we can use #define private public to bypass it and implement our own _Find_prev
Code: 55948192
For those struggling in problem Div2D, here's an alternative DP formulation, which is more aligned to the definition given in the statement
Let
dp[i] = the number of steps needed to move from room i to room (i + 1).Base case: dp[0] = 0 (we start in room 1)
For room i (1 ≤ i ≤ n):
Therefore, the recurrence relation is:
dp[i] = 2 + sum(dp[j]) for j in [p[i], i)The final answer is the
sum(dp[i]) for (1 ≤ i ≤ n).Time Complexity:
O(n^2)Optimization: While not necessary for the given constraints, we can optimize this to O(n) time complexity using prefix sums. This is the idea behind the editorial solution.