Hi Codeforces! If you calculate midpoint like
int get_midpoint(int l, int r) {//[l, r)
int pow_2 = 1 << __lg(r-l);//bit_floor(unsigned(r-l));
return min(l + pow_2, r - pow_2/2);
}
then your segment tree requires only $$$2 \times n$$$ memory.
#include <bits/stdc++.h>
using namespace std;
int get_midpoint(int l, int r) {//[l, r)
int pow_2 = 1 << __lg(r-l);//bit_floor(unsigned(r-l));
return min(l + pow_2, r - pow_2/2);
}
int n;
set<int> internal_nodes, leaf_nodes;
map<int, int> depth_of_segments_not_pow2;
void build(int v, int l, int r) {//[l, r)
if(r-l == 1) {
const int depth_leaf = __lg(v), max_depth = __lg(2*n-1);
if(l == 0) {//left-most leaf
assert(v == int(bit_ceil(unsigned(n))));
assert(depth_leaf == max_depth);
}
assert(depth_leaf == max_depth || depth_leaf == max_depth - 1);
if((n&(n-1)) == 0) assert(depth_leaf == max_depth);
assert(n <= v && v < 2*n);
assert(!leaf_nodes.count(v));
leaf_nodes.insert(v);
return;
}
if(((r-l)&(r-l-1)) == 0) assert(get_midpoint(l,r) == (l+r)/2);
else depth_of_segments_not_pow2[__lg(v)]++;
assert(1 <= v && v < n);
assert(!internal_nodes.count(v));
internal_nodes.insert(v);
int m = get_midpoint(l, r);
build(2*v, l, m);
build(2*v+1, m, r);
}
int main() {
for(n = 1; n <= 520; n++) {
cout << "n: " << n << endl;
internal_nodes.clear();
leaf_nodes.clear();
depth_of_segments_not_pow2.clear();
build(1, 0, n);
assert(ssize(internal_nodes) == n-1);
assert(ssize(leaf_nodes) == n);
for(int i = 1; i < n; i++) assert(internal_nodes.count(i));
for(int i = n; i < 2*n; i++) assert(leaf_nodes.count(i));
//at most one "bad" segment per depth
//either left child or right child (or both) will have segment length
//a power of 2; then their subtrees are a perfect binary tree
for(auto [depth, cnt] : depth_of_segments_not_pow2) assert(cnt == 1);
assert(ssize(depth_of_segments_not_pow2) <= __lg(n));
}
return 0;
}
induction assumption: the segment tree with root segment $$$[0,n)$$$ turns into a complete binary tree which has $$$2 \times n - 1$$$ nodes and max depth = __lg(2*n-1).
observe:
0 = __lg(1)
1 = __lg(2) = __lg(3)
2 = __lg(4) = __lg(5) = __lg(6) = __lg(7)
...
so
__lg(v)= depth of node vmax depth of complete binary tree = depth of any node on lowest level
node
2*n-1is always on the lowest level
Also note: get_midpoint(l + x, r + x) = get_midpoint(l, r) + x so we can "shift" any segment $$$[l,r)$$$ to $$$[0,r-l)$$$ and the corresponding segment trees have the same structure, hint: min(a + x, b + x) = min(a, b) + x
Induction step
case 0: $$$r-l$$$ is a power of 2
get_midpoint(l,r) returns $$$\dfrac{r+l}{2}$$$, and we get a perfect binary tree (which is also complete).
case 1: $$$l + pow2 < r - \frac{pow2}{2}$$$
$$$[l,r)$$$ splits into:
left child with segment $$$[l,l+pow2)$$$, (from induction assumption and "shift"-ing) a complete binary tree with max depth =
__lg(2*pow2-1)right child with segment $$$[l+pow2, r)$$$, (from induction assumption and "shift"-ing) a complete binary tree with max depth =
__lg(2*((r-l) - pow2)-1)
steps:
$$$ \frac{pow2}{2} < (r-l) - pow2$$$ (rearange case assumption)
$$$\frac{1}{2} \times (r-l) < pow2$$$ ($$$pow2$$$ is defined/calculated as: largest power of 2 $$$ \le (r-l)$$$ )
$$$(r-l) - pow2 < pow2$$$ (from step 2, multiply by 2, then subtract $$$pow2$$$)
$$$\frac{pow2}{2} < (r-l) - pow2 < pow2$$$ (combine steps 1,3)
$$$pow2 \le 2 \times ((r-l) - pow2) - 1 < 2 \times pow2-1$$$ (from step 4, multiply by 2, then subtract 1)
__lg(pow2)=__lg(2*((r-l) - pow2) - 1)=__lg(2*pow2-1)(from step 5, take log2; think about their binary representation)
From this, the left and right childs have the same max depth; the left child is a perfect binary tree; the right child is a complete binary tree, so overall it's a complete binary tree.
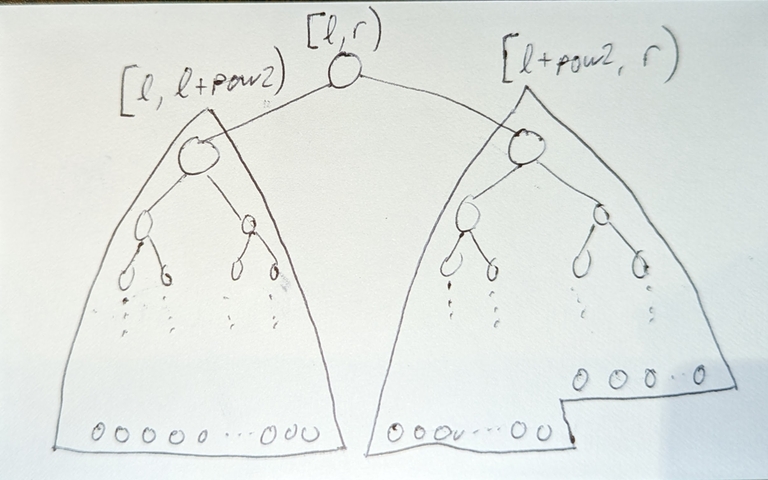
case 2: $$$l + pow2 \ge r - \frac{pow2}{2}$$$
$$$[l,r)$$$ splits into:
left child with segment $$$[l, r - \frac{pow2}{2})$$$, (from induction assumption and "shift"-ing) a complete binary tree with max depth =
__lg(2*((r-l) - pow2/2)-1)right child with segment $$$[r - \frac{pow2}{2}, r)$$$, (from induction assumption and "shift"-ing) a complete binary tree with max depth =
__lg(2*(pow2/2)-1)
steps:
$$$(r-l) - \frac{pow2}{2} \le pow2$$$ (rearange case assumption)
$$$pow2 < (r-l)$$$ ($$$pow2$$$ is defined/calculated as: largest power of $$$2 \le (r-l)$$$, see case 0 for when $$$(r-l)$$$ is a power of 2)
$$$\frac{pow2}{2} < (r-l) - \frac{pow2}{2}$$$ (from step 2, subtract $$$\frac{pow2}{2}$$$)
$$$\frac{pow2}{2} < (r-l) - \frac{pow2}{2} \le pow2$$$ (combine steps 1,3)
$$$pow2 \le 2 \times ((r-l) - \frac{pow2}{2}) - 1 \le 2 \times pow2-1$$$ (from step 4, multiply by 2, subtract 1)
__lg(pow2)=__lg(2*((r-l) - pow2/2) - 1)=__lg(2*pow2-1)(from step 5, take log2; think about their binary representation)__lg(2*((r-l) - pow2/2) - 1)=__lg(pow2)= 1 +__lg(pow2/2)= 1 +__lg(2*(pow2/2)-1)(from step 6, using log rules)
From this, the left child has max depth = 1 + right child max depth. The left child is a complete binary tree; the right child is a perfect binary tree, so overall, it's a complete binary tree.
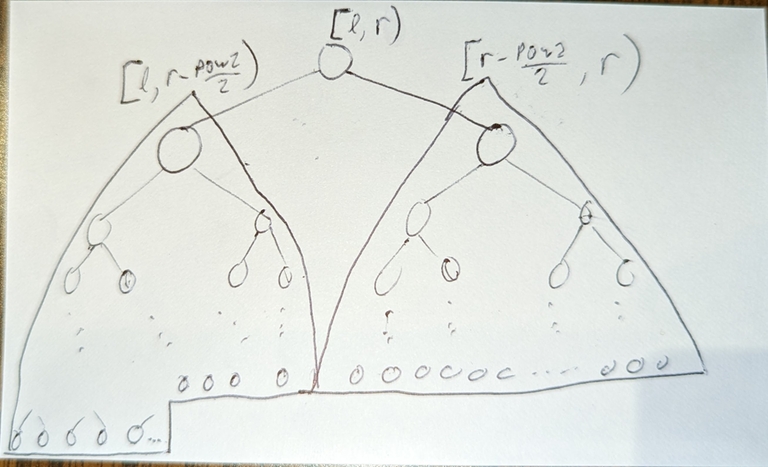
I was inspired by ecnerwala's in_order_layout https://github.com/ecnerwala/cp-book/blob/master/src/seg_tree.hpp
I'll be waiting for some comment "It's well known in china since 2007" 😂











It's well known in china since 2007
Thats cool, you're decomposing the segtree into perfect binary trees, not actually caring if the sizes are the same. It gives me some new intuition on the subject.
maybe you want this Efficient and easy segment trees
Segment tree is always 2n memory. I don't get what is new...
I think recursion makes it nlogn. Edit: why did I get downvoted? I'm probably wrong so can you point out my mistake instead of downvoting?
Most implementations take 4n memory.
In fact you can label [l, r] with (l + r | (l != r)), the labels also lay in [2, 2n]
You can do this also: let the root be the node $$$0$$$ and let the neighbors for any node $$$x$$$ be $$$x + 1$$$ for the left child, and $$$x + 2(m - l + 1)$$$ for the right child (where $$$[l, r] $$$ is the range which node $$$x$$$ is responsible for, and $$$m$$$ is $$$(l + r) / 2$$$). Also, this is exactly the DFS traversal order of the segment tree.
That's a really cool trick. It should also slightly improve cache hits when going to the left son (although not by a large amount). This is how tourist's segment tree is implemented, btw.
This trick is actually pretty cool. I played around with this for a while and got AC a sweepline problem that I got MLE weeks ago. With that said, is there any way, any more tricks that could make this thing faster? Like, I benchmark this method of choosing mid-point, versus the classic method and the latter is around 20% faster, despite consuming twice as much memory (probably because the old method divide the segment into half, making the $$$log$$$ constant per query smaller). Is there any kind of recursive segment tree implementation that is both fast and memory-efficient at the same time?