Предлагаю здесь обсудить задачи прошедшего Гран-При.
Интересно, как решать I? Мы дошли до того что, эта операция это умножение на простенькую матрицу в кольце по модулю 2. Но непонятно какой у нее период.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Предлагаю здесь обсудить задачи прошедшего Гран-При.
Интересно, как решать I? Мы дошли до того что, эта операция это умножение на простенькую матрицу в кольце по модулю 2. Но непонятно какой у нее период.
| Название |
|---|



I: Пусть есть бесконечная в обе стороны строка s0. Применяем к ней последовательно нашу операцию, получаем строки s1, s2, ... Легко доказать по индукции, что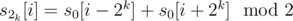 .
.
Сделаем из исходной строки t0 строку s0 как ... + t0 + 0 + reverse(t0) + 0 + t0 + .... Если из t0 данной операцией получаются строки t1, t2, ..., то si = ... + ti + 0 + reverse(ti) + 0 + ti + .... Теперь очевидно, как посчитать tk за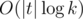 .
.
Посмотрим на матрицу, домножением на которую является это преобразование. По каким-то причинам, в ее степенях вида 2k в каждой строке и столбце не более, чем 2 не нуля. (видимо примерно по тем, которые ты описал). Значит, ее можно возводить в квадарт за линию. Перемножить получится за O(logT * n), если перемножать со столбцом, а не матрицы между собой и потом на столбец.
Ну, это какая-то магия вида "заметим, что". Можно ничего не замечать. =)
На самом деле там легко доказать по индукции, поэтому не магия
Добрый вечер всем. Может кто-нибудь рассказать правильное решение задачи F? Писали нахождение эйлерова пути влоб, получили мл16, убрали построение графа в явном виде — получили тл16, начали по-другому кодировать состояния — получили тл17, дооптимайзили до тл18. В запуске на КФ работает ~2.5 сек, тл на задачу — 5 сек. Пропихивается ли такое? или правильное решение другого плана ? За ранее спасибо.
Я думаю, все же речь идет о гамильтоновом пути, а не о эйлеровом. Мы сдали такое, напишем обычный перебор, только перебирая очередной переход, сначала пытаемся выбрать такие, которые добавляют в маску единичку, а потом только убирают. Как-то так
OOPS: Задачка оказалась проще, а мы находили гамильтонов путь, в графе, где ребра это вершины и наоборот =)
Обычный эйлеров путь заходит, если не перебирать в каждой вершине 18 исходящих ребер (что работает за 182 * 218), а сразу удалять использованные ребра. Наверное, еще возможны проблемы с большим выводом.
Можно еще для каждой вершины иметь глобальный указатель на следущее просматриваемое ребро
Вроде-бы так и делали. Тл18.
По своей глупости, для того что бы сделать переход из вершины — каждую итерацию декодировали текущую вершину, и потом уже переходили в другое состояние. Вынеся декодирование (5 итераций) за цикл переходов — получил ОК. В запуске на КФ это сэкономило 250 мс... С этой "оптимизацией" : Использовано: 1872 мс, 63604 КБ (ОК) без нее: Использовано: 2120 мс, 63600 КБ (ТЛ18) P.S. Всем спасибо за ответы!
Проще всего пройти все переключатели кодом Грея, затем идти по нему же назад, проходя в каждой вершине по всем ребрам, не принадлежащим коду Грея, вперед и назад.
Мы написали честный эйлеров цикл: обходим весь граф dfs'ом (218 вершин), при выходе из вершины добавляем ребро, по которому выходим, в ответ. Так как для каждого ребра есть симметричное, то всё равно, идти ли по обратным или по прямым.
У нас еще локально падал стэк, написали dfs на ручном стэке.
расскажите K
Мы писали следущее: Будем поддерживать точку в виде линейной комбинации x0,y0,1. Проецируем честно n раз. Далее решаем гаусса 3 на 3(условие того, что мы пришли в исходную точку и что точка лежит на исходной прямой)
Простой тернарный поиск проходит. Тернарный поиск запускаем по x-координате первой прямой. Если же первая прямая имеет вид x=C, то запускаем по y-координате.
В тернарке стараемся минимизировать расстояние от точки, в которую пришли, до точки, в которой начали?
Почему в такой ситуации не делать поиск по расстоянию от точки на первой прямой, которая лежит где-то на условной бесконечности?
Да, минимизируем расстояние от начальной точки до той, в которую пришли.
Второй вопрос немного не понял. Нам же важно, из какой точки мы стартуем и тернарный поиск именно по x-координате этой точки.
Задаем точку-ответ параметрически по первой прямой: At+B. Проецируем n раз, получаем уравнение A_n*t + B_n = A*t + B, оно линейно по t, решаем.
UPD: t = (B.x — B_n.x) / (A_n.x — A.x) если (A_n.x — A.x != 0)
А как в J адекватно поддерживать высоты при удалении вершины с одним ребенком?
Можно не удалять вершину, а помечать ее 0/1, и считать сумму на пути до корня.
Первым проходом сделаем все операции с деревом, не обращая внимания на глубины.
От полученного дерева построим структуру данных, которая за logn умеет изменять вес вершины и за те же logn искать сумму на пути до корня. Например изменить вес вершины: += к поддереву, а это += на отрезке.
Мы честно хранили эйлеров обход в декартовом дереве. Тогда высота — это сумма на префиксе. А все операции это какие-то доваления/удаления ребер.
Угу, я примерно о том же, только у меня offline, поэтому дерево отрезков.
My approach for M: lets have priority_queue PQ where we keep people we can buy their loyalty (considering current value of M) with the key r[i]-c[i] and multiset SET where we keep people who cannot be bought in this moment with the key c[i].
Then we remove and/or move elements from these data structures greedily.
Any better solution?
А как решалась задача A?
Напишем перебор =) Можно доказать, что есть всего два варианта перехода: взять предыдущий элемент, который мы уже взяли или взять 2S + 1, где S текущая набранная сумма. Ну и, естественно, мы отсекаемся, когда S становится больше N.
код
PS: Ну и первым всегда берем 1.
Вот так
Если подробнее. В отсортированном ответе каждое число равно либо предыдущему, либо удвоенной сумме предыдущих + 1.
Почему это так. Из чисел любого префикса можно получить все до суммы. По индукции. Почему не подходит другое. Если очередное число больше, то нельзя получить N — 2*sum — 1. Если меньше, то x — Sum можно получить двумя способами.
Перебор отрабатывает быстро, потому что написали и проверили.
Кстати даже отсечение по ответу не обязательно делать, это все равно залетает. На contest.yandex.ru с отсечением и без него отрабатывает за 26ms.
Каждое новое число, не равное предыдущему, равно 2S + 1, где S~--- сумма всех предыдущих. Это значит, что N = S + k(2S + 1), или 2N + 1 = (2k + 1)(2S + 1). Поскольку первые числа дают хорошее множество с суммой S, верно, что 2S + 1 = (2k' + 1)(2S' + 1), и т.д. В итоге 2N + 1 = (2k + 1)(2k' + 1)(2k" + 1)..., т.е. какое-то разложение 2N + 1 на нечетные множители. Поскольку длина ответа равна k + k' + k" + ..., и мы ее минимизируем, это разложение на простые множители в каком-то порядке.
Пример: N = 52, 2N + 1 = 105 = 3 × 5 × 7.
52 = 1 + 3 + 3 + 15 + 15 + 15
52 = 1 + 3 + 3 + 3 + 21 + 21
52 = 1 + 1 + 5 + 15 + 15 + 15
52 = 1 + 1 + 5 + 5 + 5 + 35
52 = 1 + 1 + 1 + 7 + 21 + 21
52 = 1 + 1 + 1 + 7 + 7 + 35
С задачей А меня больше всего убивает тот факт, что она решается абсолютно так же, как и задача про гирьки с прошлогоднего же ICL с точностью до косметических изменений.
Её вполне можно решить без перебора. Рассуждаем следующим образом. Упорядочим веса существующих гирек по возрастанию — w1, w2, ..., wk. Пусть гирек веса wi у нас ai штук. Тогда любое состояние весов описывается вектором (x1, x2, ..., xk), где - ai ≤ xi ≤ ai, причём по условию соответствие взаимно однозначное. С одной стороны мы должны уметь взвесить все веса от - N до N, которых 2N + 1 штук. С другой, всевозможных векторов — (2a1 + 1)(2a2 + 1)... (2ak + 1). Значит, 2N + 1 = (2a1 + 1)(2a2 + 1)... (2ak + 1).
Дальше замечаем, что при фиксированных a1, a2, ..., ak веса w1, w2, ..., wk восстанавливаются однозначно (w1 = 1, а каждый последующий должен быть на единицу больше удвоенного максимального веса, который можно получить предыдущими).
Значит, нам надо найти все разбиения, при которых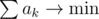 . С другой стороны, каждое разбиние — это какое-то разложение 2N + 1 на множители. Теперь надо понять, что для минимизации суммарного количества гирек множители в разложении должны быть простыми. Это следует из следующего неравенства: пусть у нас есть множитель (2ai + 1) = (2x + 1)(2y + 1). Заменим это ai на x и y — тогда
. С другой стороны, каждое разбиние — это какое-то разложение 2N + 1 на множители. Теперь надо понять, что для минимизации суммарного количества гирек множители в разложении должны быть простыми. Это следует из следующего неравенства: пусть у нас есть множитель (2ai + 1) = (2x + 1)(2y + 1). Заменим это ai на x и y — тогда 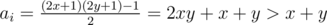 , т. е. выгодно разбить составной множитель на два простых.
, т. е. выгодно разбить составной множитель на два простых.
Ну и выходит, что каждое разбиение однозначно соответствует какой-то перестановке строки p1, p2, ... pu, состоящей из простых множителей 2N + 1 с учётом кратности. По перестановке ответ восстанавливается простым проходом за O(u). Получилось решение за факторизацию плюс перебор перестановок простых множителей.
Мне очень нравится эта красивая математическая конструкция, только не очень нравится тот факт, что я дословно те же рассуждения проводил год назад, писал дословно то же решение, и даже исправлял по ходу написания те же баги :-)
Кстати, как доказать, что хотя бы одна единица нужна? Почему ее нельзя представить как 3 - 2, например?
Если у нас есть набор с сумой S, и в нём нет 1, тогда мы не можем представить суму S — 1.
Да, действительно. Спасибо.
У меня вот был какой-то не совсем перебор.
Факт 1: Всегда нужно взять 1.
Док-во: Иначе мы не сможем взвесить N-1.
Факт 2: Если отсортировать гирьки по неубыванию веса, то первая гирька — 1, а (k+1)-ая либо равна k-ой, либо равна 2S+1, где S — сумма префикса длины k.
Док-во: Будем доказывать по индукции, попутно поддерживая тот факт (2*), что гирьками с префикса можно единственным образом взвесить все массы до S включительно.
База индукции верна (из факта 1). Пусть k-ая гирька была веса Х, мы хотим поставить гирьку веса Y. Нам нужно показать, что либо Y=X, либо Y=2S+1. Очевидно, Y>=X. Пусть Y>2S+1. Тогда мы не сможем взвесить N-(2S+1). Пусть X<Y<2S+1, тогда либо Y, либо Y-S представимо не одним способом. Док-во (2*) очевидно.
Теперь пусть мы поставили k единиц (а затем не единицу). Тогда по индукции очевидно, что далее на любом префиксе S = k (mod (2k+1) ), а так же любой последующий элемент делится на (2k+1). Если N-k не делится на (2k+1), то для такого k решений нет. Иначе выкинем все единицы, а так же разделим все на (2k+1).
Теперь нам нужно решить ту же самую задачу для (N-k)/(2k+1).
Напишем ленивую динамику, получим АС.
Может кто-нибудь поделиться своим подходом к решению задачи Д? Может есть какая-то красивая конструкция (как та, которую выше привел Endagorion)?
Я решал в общем виде, вычисляя операции, которые необходимо провести со списком бактерий, чтобы получить позицию через 2k секунд. Пример для пяти бактерий:
При этом каждая следующая операция вычисляется применением предыдущей операции к самой себе. Например, если мы применим a0+a2 (третья строка) к самой последовательности, то получим a0 + a2 + a0 + a4 = a2 + a4. Итоговый ответ получается последовательным применением операций для нужных степеней двойки к исходной последовательности бактерий.
M (каръера Джимми, Div. 2 only) — прошло всего 13/238 субмитов. Кто может поделиться решением? (Моё ошибается на первом тесте — ideone Perl)
C (динозавры) — решил так: 1) число перевел в 2-чную систему счисления, 2) приписал 0 к началу, 3) развернул, 4) искал и изменял подстроки из ноля и более чем одной еденицы (110, 111110) на подстроки из еденицы, нолей и минус еденицы (-101, -100001), 5) разбил по цифрам, развернул обратно. (Perl ideone).
В задаче M нами была обнаружена предположительная ошибка в тестах. В условии сказано, что до символа ':' цифр нет. Мы парсили через istringstream путем замены всех не цифр на пробелы. С правильным решением получали WA 2. После контеста мы считывали числа после ':' и получили OK. Проверили assert-ом наличие цифр до двоеточия и оказалось что они там есть. Подали апелляцию на эту задачу, надеюсь на rejudge.