Завтра в 19:00 по Москве состоится SRM #613. Не пропустите!
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
12:02:36
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
12:02:36
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 05:32:24 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











I almost solved 500. I realized my silly mistake too late to change it. Wait and see as I reach red by always solving just the easiest problem :D
My idea was pretty much DP + inclusion-exclusion principle. It's clear that if we replace low by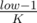 and high by
and high by 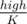 , then we just need to find the number of sequences with elements in (low, high] whose GCD=1.
, then we just need to find the number of sequences with elements in (low, high] whose GCD=1.
Let dp[d] be the number of sequences whose GCD equals d. We can transform low and high in a similar manner (except it's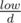 and
and 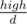 ) and find out the total number of such sequences: (high - low)N by modular exponentiation. Then, we just need to try all GCDs that are multiples of d (kd, at least 2d) and subtract dp[kd] from dp[d]. We can even afford to use
) and find out the total number of such sequences: (high - low)N by modular exponentiation. Then, we just need to try all GCDs that are multiples of d (kd, at least 2d) and subtract dp[kd] from dp[d]. We can even afford to use
map<>to store the DP.This is too slow, so let's just try divisors that aren't > high - low. For any other divisors, all the elements of any array with a suitable GCD are equal (there can't be 2 distinct elements in the corresponding range), so we can modify the DP to store (in dp[d]) just the number of sequences with at least 2 distinct elements; the total number of sequences also decreases by high - low. The answer now is dp[1], plus 1 if 1 can be an element of the array (an array of 1s also has GCD=1).
My mistake was not checking the sequences with distinct elements separately. Shit happens...
UPD: The time complexity of this approach is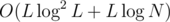 , where L = high - low after the initial transformation (taking K to 1). That's because we access the DP states
, where L = high - low after the initial transformation (taking K to 1). That's because we access the DP states 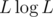 times in total, where each access costs
times in total, where each access costs 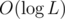 per
per
map<>access or insertion, plus run modular exponentiation once per each DP state.Since the DP states (as used here) take 1 parameter d ≤ L, we can use a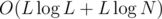 .
.
vector<>instead of amap<>, which gives a runtime ofcode
I think we can pass the slow approach by using unordered_set in c++.
The transition to vectors is a matter of less than a minute, and is faster and simpler than hash tables. But I used a map during the contest, because I wasn't sure about the form of the DP when I made that decision. I code first and see what I coded second.
Could you give more details about this ? I don't really understand it :(
Do you understand the part before this? If you do, then it's easy. Just think about the DP as computing "the number of sequences with at least 2 distinct elements and GCD equal to d" (when all elements that you can choose are multiples of d) and think how it has to work. You compute the total number of sequences (with GCD being any multiple of d), subtract the number of sequences with all elements identical, and then subtract the number of all sequences with at least 2 distinct elements but bad GCD. And those are counted in larger DP states.
The answer you'd get by this DP can be off by 1 — if you can make a sequence consisting of all 1s, this would also have GCD=1, and contributes +1 to the correct answer. Add it if necessary.