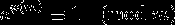Hi, I am having problem with solving this task from my math homework. If number p is prime and p^2+8 is also prime. Prove that p^3+4 is also prime number.
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3810 |
| 2 | Benq | 3676 |
| 3 | Kevin114514 | 3655 |
| 4 | maroonrk | 3463 |
| 5 | strapple | 3390 |
| 6 | Um_nik | 3387 |
| 7 | tourist | 3384 |
| 8 | heuristica | 3322 |
| 9 | turmax | 3319 |
| 10 | jiangbowen | 3291 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | Qingyu | 156 |
| 2 | nik_exists | 150 |
| 2 | maspy | 150 |
| 4 | Um_nik | 144 |
| 5 | Errichto | 139 |
| 6 | adamant | 137 |
| 6 | AmShZ | 137 |
| 8 | BledDest | 132 |
| 8 | maroonrk | 132 |
| 10 | qwexd | 129 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2026 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Sep/27/2026 08:05:11 (g2).
Desktop version, switch to mobile version.
Supported by
Suppose that p ≠ 3. Then
thus p2 + 8 is not prime and we were wrong in our assumption. Then p = 3 and p3 + 4 = 31 which is obviously prime.
How to prove that p2 = 1 mod 3?
Fermat's little theorem. If p is prime, then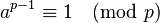
This is a special case of Euler's theorem, which is formulated like this for coprime a, m:
