Блог пользователя UltramanDecker

Need help for a tree problem
Автор UltramanDecker, история, 2 года назад, По-английски

Given a tree with $$$N$$$ nodes. The tree nodes are numbered from $$$1$$$ to $$$N$$$.

For each node $$$i$$$, please print how many paths that $$$i$$$ is the maximum node in this path.

For example in a tree

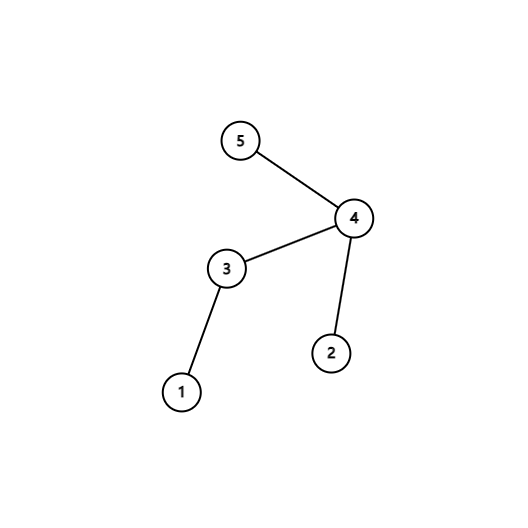
For node 4, in paths {2,4,3} {2,4,3,1} {4,3,1} {4,2} {4,3} {4}, 4 is the maximum node in these paths, so the answer for node 4 is 6.

I want to know is there any $$$O(n)$$$ or $$$O(NlogN)$$$ solutions and how to solve it.

Thank you all!

  • Проголосовать: нравится
  • +8
  • Проголосовать: не нравится

»
2 года назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

Assuming I've not misunderstood and {4,3,2} is a valid path and the answer should be 6:

Order the edges by the larger of the two end points and add them 1 at a time. Use DSU to keep track of size of connected components. Initialise all the answers to 1 (every node has a path with itself in).

Every adge would then join two connected components (possibly of size 1) and add the product of their sizes to the answer for the larger node on this edge.

eg on the above graph you get the following edges in order (3,1), (4, 2), (4,3), (5, 4)

Initial answer is (1,1,1,1,1)


Adding (3,1): Answer is (1,1,2,1,1) (connect components (3) and (1) for +1 to 3)
Adding (4,2): Answer is (1,1,2,2,1) (connect components (2) and (4) for +1 to 4)
Adding (4,3): Answer is (1,1,2,6,1) (connect components (4,2) and (1,3) for +4 to 4)
Adding (5,4): Answer is (1,1,2,6,5) (connect components (5) and (1,2,3,4) for +4 to 5)
→ Ответить
»
2 года назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Auto comment: topic has been updated by UltramanDecker (previous revision, new revision, compare).

→ Ответить