UltramanDecker's blog

Need help for a tree problem
By UltramanDecker, history, 2 years ago, In English

Given a tree with $$$N$$$ nodes. The tree nodes are numbered from $$$1$$$ to $$$N$$$.

For each node $$$i$$$, please print how many paths that $$$i$$$ is the maximum node in this path.

For example in a tree

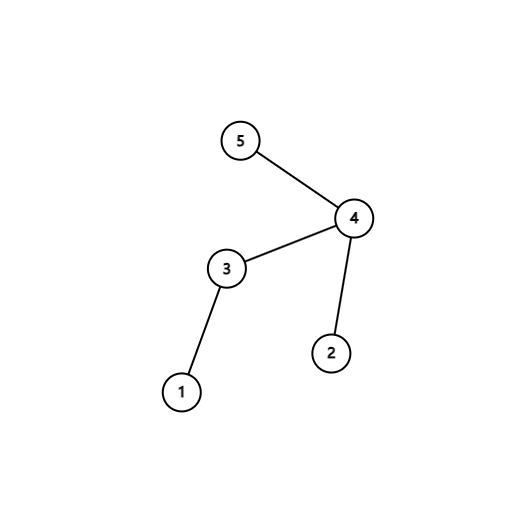
For node 4, in paths {2,4,3} {2,4,3,1} {4,3,1} {4,2} {4,3} {4}, 4 is the maximum node in these paths, so the answer for node 4 is 6.

I want to know is there any $$$O(n)$$$ or $$$O(NlogN)$$$ solutions and how to solve it.

Thank you all!

  • Vote: I like it
  • +8
  • Vote: I do not like it

»
2 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Assuming I've not misunderstood and {4,3,2} is a valid path and the answer should be 6:

Order the edges by the larger of the two end points and add them 1 at a time. Use DSU to keep track of size of connected components. Initialise all the answers to 1 (every node has a path with itself in).

Every adge would then join two connected components (possibly of size 1) and add the product of their sizes to the answer for the larger node on this edge.

eg on the above graph you get the following edges in order (3,1), (4, 2), (4,3), (5, 4)

Initial answer is (1,1,1,1,1)


Adding (3,1): Answer is (1,1,2,1,1) (connect components (3) and (1) for +1 to 3)
Adding (4,2): Answer is (1,1,2,2,1) (connect components (2) and (4) for +1 to 4)
Adding (4,3): Answer is (1,1,2,6,1) (connect components (4,2) and (1,3) for +4 to 4)
Adding (5,4): Answer is (1,1,2,6,5) (connect components (5) and (1,2,3,4) for +4 to 5)
→ Reply
  • »
    »
    2 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    my fault for path {2,4,3}, sorry

    and thank you very much for the solution, I think I finally got it!

    → Reply
»
2 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by UltramanDecker (previous revision, new revision, compare).

→ Reply