Benchmarks of different segment tree implementations

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
4	atcoder_official	161
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Sometimes I wonder, what implementation of a segment tree to use. Usually, I handwave that some will suit, and that works in most of the cases.

But today I decided to back up the choice with some data and I ran benchmarks against 4 implementations:

Simple recursive divide-and-conquer implementation

Code

struct SimpleRecursiveSegmentTree {
    unsigned size;

  private:
    std::vector<long long> t;

    void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {
        if (r == l + 1) {
            t[p] = v[l];
            return;
        }
        unsigned m = (l + r) / 2;
        _build(v, 2 * p + 1, l, m);
        _build(v, 2 * p + 2, m, r);
        t[p] = t[2 * p + 1] + t[2 * p + 2];
    }

    long long _get(unsigned p, unsigned l, unsigned r, unsigned a,
                   unsigned b) const {
        if (b <= l || r <= a) {
            return 0LL;
        }
        if (a <= l && r <= b) {
            return t[p];
        }
        unsigned m = (l + r) / 2;
        return _get(2 * p + 1, l, m, a, b) + _get(2 * p + 2, m, r, a, b);
    }

    void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {
        if (i < l || r <= i) {
            return;
        }
        if (r == l + 1) {
            t[p] += x;
            return;
        }
        unsigned m = (l + r) / 2;
        _add(2 * p + 1, l, m, i, x);
        _add(2 * p + 2, m, r, i, x);
        t[p] = t[2 * p + 1] + t[2 * p + 2];
    }

  public:
    SimpleRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {
        t.resize(4 * size);
    }

    SimpleRecursiveSegmentTree(const std::vector<int> &v) noexcept
        : size(v.size()) {
        t.resize(4 * size);
        _build(v, 0, 0, size);
    }

    void add(unsigned i, int x) { _add(0, 0, size, i, x); }

    long long get(unsigned l, unsigned r) const {
        return _get(0, 0, size, l, r);
    }
};

Optimized recursive divide-and-conquer, which does not descend into apriori useless branches

Code

struct OptimizedRecursiveSegmentTree {
    unsigned size;

  private:
    std::vector<long long> t;

    void _build(const std::vector<int> &v, unsigned p, unsigned l, unsigned r) {
        if (r == l + 1) {
            t[p] = v[l];
            return;
        }
        unsigned m = (l + r) / 2;
        _build(v, 2 * p + 1, l, m);
        _build(v, 2 * p + 2, m, r);
        t[p] = t[2 * p + 1] + t[2 * p + 2];
    }

    long long _get(unsigned p, unsigned l, unsigned r, unsigned a,
                   unsigned b) const {
        if (a <= l && r <= b) {
            return t[p];
        }
        unsigned m = (l + r) / 2;
        long long res = 0;
        if (a < m) {
            res += _get(2 * p + 1, l, m, a, b);
        }
        if (b > m) {
            res += _get(2 * p + 2, m, r, a, b);
        }
        return res;
    }

    void _add(unsigned p, unsigned l, unsigned r, unsigned i, int x) {
        if (r == l + 1) {
            t[p] += x;
            return;
        }
        unsigned m = (l + r) / 2;
        if (i < m) {
            _add(2 * p + 1, l, m, i, x);
        } else {
            _add(2 * p + 2, m, r, i, x);
        }
        t[p] = t[2 * p + 1] + t[2 * p + 2];
    }

  public:
    OptimizedRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {
        t.resize(4 * size);
    }

    OptimizedRecursiveSegmentTree(const std::vector<int> &v) noexcept
        : size(v.size()) {
        t.resize(4 * size);
        _build(v, 0, 0, size);
    }

    void add(unsigned i, int x) { _add(0, 0, size, i, x); }

    long long get(unsigned l, unsigned r) const {
        return _get(0, 0, size, l, r);
    }
};

Non-recursive implementation (credits: https://codeforces.me/blog/entry/18051)

Code

struct NonRecursiveSegmentTree {
    unsigned size;

  private:
    std::vector<long long> t;

    void _build(const std::vector<int> &v) {
        std::copy(v.begin(), v.end(), t.begin() + size);
        for (int i = size - 1; i > 0; --i) {
            t[i] = t[i * 2] + t[i * 2 ^ 1];
        }
    }

  public:
    NonRecursiveSegmentTree(unsigned _size) noexcept : size(_size) {
        t.resize(2 * size);
    }

    NonRecursiveSegmentTree(const std::vector<int> &v) noexcept
        : size(v.size()) {
        t.resize(2 * size);
        _build(v);
    }

    void add(unsigned i, int x) {
        i += size;
        for (t[i] += x; i > 1; i /= 2) {
            t[i / 2] = t[i] + t[i ^ 1];
        }
    }

    long long get(unsigned l, unsigned r) const {
        long long res = 0;
        for (l += size, r += size; l < r; l /= 2, r /= 2) {
            if (l & 1) {
                res += t[l++];
            }
            if (r & 1) {
                res += t[--r];
            }
        }
        return res;
    }
};

Fenwick Tree

Code

struct FenwickTree {
    unsigned size;

  private:
    std::vector<long long> t;

    long long get_prefix(int i) const {
        long long res = 0;
        while (i >= 0) {
            res += t[i];
            i = (i & (i + 1)) - 1;
        }
        return res;
    }

  public:
    void add(unsigned i, int x) {
        while (i < size) {
            t[i] += x;
            i = i | (i + 1);
        }
    }

    FenwickTree(unsigned _size) : size(_size) { t.resize(size); }

    FenwickTree(const std::vector<int> &v) : size(v.size()) {
        t.resize(size);
        for (unsigned i = 0; i < size; ++i) {
            add(i, v[i]);
        }
    }

    long long get(unsigned l, unsigned r) {
        return get_prefix((int)r - 1) - get_prefix((int)l - 1);
    }
};

All implementations are able to:

get(l, r): get sum on a segment (half-interval) $$$[l; r)$$$
add(i, x): add $$$x$$$ to the element by index $$$i$$$

Here are the results: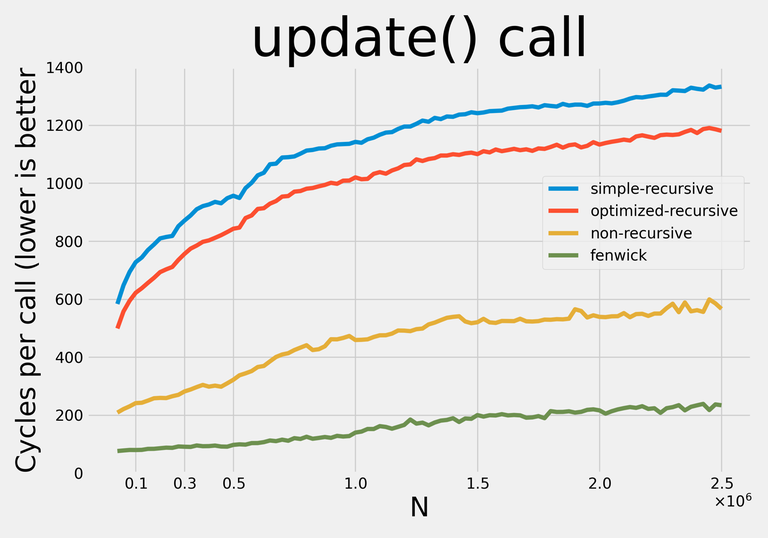

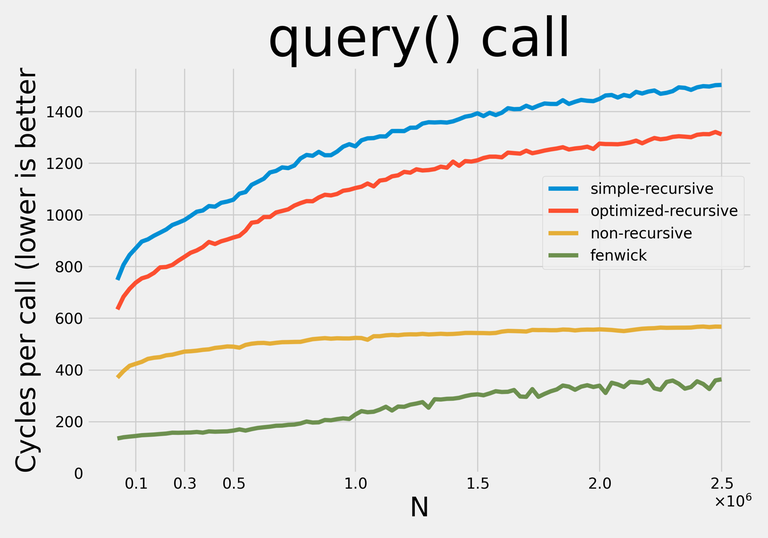
Note: I decided not to apply any addition-specific optimizations so that with minor modifications the data structures could be used for any supported operations.

I generated queries the following way:

Update: generate random index (rnd() % size) and number
Query: at first, generate random length (rnd() % size + 1), then generate a left border for that length

Benchmarking source code. Note that ideally you should disable frequency scaling, close any applications that might disrupt the benchmark (basically, the more you close — the better) and pin the benchmark process to a single CPU (core).

Plot-generating Python script

My benchmarking data in case you want to do some more plotting/comparing.

I compiled the benchmark with #pragma GCC optimize("O3") on GNU GCC 11.3.0, and ran it with the CPU fixed on 2.4 GHz, the process pinned on a single CPU core and the desktop environment closed.

This is probably my first useful contribution so any suggestions/improvements are welcome.

Comments (11)

Show archived | Write comment?

pavook

2 years ago, # |

Auto comment: topic has been updated by pavook (previous revision, new revision, compare).

→ Reply

AndreyPavlov

+17

All good, but benchmark have 1 error: Fenwick != Segment tree

2 years ago, # ^ |

Although it's technically true, Fenwick tree and non-recursive segment tree are similar both in structure and in performance. It's also a frequent "dilemma": implementing Fenwick tree or segment tree, so its addition felt appropriate.

I do not consider the Fenwick tree and the non-recursive segment tree to be similar in structure.

sslotin

+29

You can think of a Fenwick tree as a complete segment tree with all right children removed.

tiom4eg

Even if it's true, you still can't perform many types of complex operations using Fenwick tree, so imho Fenwick tree is quite useless for regular contests... Anyway, thanks for the blog, it was really interesting :)

lis05

Fenwick tree is useful when TL is tight or (if the task allows) if writing a Segment tree will be too long.

s-lissov

-12

I think a pointer-based segment tree is missing.

ftiasch

+14

Thanks for the job you have already done!

However, in my option, it doesn't provide any useful information. It's more a toy research project as you eventually learn different segment tree implementation than a serious benchmark because it simply says something like recursive > non-recursive > fenwick as expected with g glance.

To improve, I list several possible direction here:

The asymptotic complexity is $$$O(n \log n)$$$ with derivatives $$$\log n + 1 > 0$$$ which means the curve should be convex. However, the plot shows somehow counter-intuitively a concave curve. I suggest to plot against $$$\mathrm{time} / n \log n$$$ or use log-scaled $$$n$$$-axis which may end up with a plausible result or find serious drawdark of the existing plotting.
Try to generate more testsuits instead of simply randomly generated data. For example, is there any carefully crafted data point which causes significant performance downgrade, like to introduce unexpected high ratio of cache misses?
Try to compare different segment tree operations besides simple additions. How does the complexity of the basic operations affects the overall speed?
Simply fixing the cpu frequency and turning off graphical environment does not mean sufficient. First of all, what's your CPU model? and what's the instruction set? Did it run in the full-power mode? Did you pin cpu core to avoid context switching? And we know that segment tree presents large amount of memory access. So you should also provides the information about memory. I think it's better the breakdown the part into cpu computation and memory accessing, and carefully measure metrics like cache misses.

← Rev. 2 →

Thank you very much for the suggestions.

I think L2/L3 cache sizes had their impact on this result along with other things like branch misses. Here are the plots divided by $$$\log n$$$:
Plots

Notably, non-recursive query has a remarkably constant constant :).

The sudden jumps in update constant plot you can see (at $$$N \approx 275000$$$ for recursive implementations, at $$$N \approx 450000$$$ for non-recursive implementation) align quite nicely with tree sizes beginning not to fit in my 8M L3 Cache.

I couldn't figure anything else special about the plots, so any help/ideas would be appreciated.
I don't know even how to approach this suggestion. I'm sure it's very hard to figure out performance-intensive tests with pure random and I'm too stupid for evolution or simulated annealing approaches.
I think I will do this eventually. I'll try to post updates somewhere here.
CPU model: Intel(R) Core(TM) i5-1135g7. I did run it in full-power mode (perf-bias set to 0 and perf-policy set to performance). I reran the benchmark with pinning the process to a CPU core using taskset, thank you for this advice.

About cache misses and other advanced metrics: I feel like that information would be quite a pain in the butt to collect. I don't know how to measure those metrics except for tools like perf. But if I'm going use perf or something similar, I'll need to run all the instances separately and collect the results separately. That would really blow up the complexity of running the benchmark.

pavook's blog