We will hold AtCoder Beginner Contest 243.
- Contest URL: https://atcoder.jp/contests/abc243
- Start Time: http://www.timeanddate.com/worldclock/fixedtime.html?iso=20220312T2100&p1=248
- Duration: 100 minutes
- Number of Tasks: 8
- Writer: kyopro_friends,leaf1415, blackyuki,Nyaan
- Tester:math957963,sugarrr
- Rated range: ~ 1999
- The point values will be 100-200-300-400-500-500-600-600.
We are looking forward to your participation!










How to solve E ? I did floyd warshall and got WA.
you use floyd warshall, but most likely u didnt find shortest paths with as many edges as possible, cuz i didnt do that at first and i got wa as well. basically instead of if(dist[i][j]>dist[i][k]+dist[k][j]), you should have >=. If you have a graph like the one shown below, you won't delete any edges even though you can remove edge from 2-4 because fw will find that the shortest path is the edge of 2-4, when you want fw to find that the shortest path is 2->3, then 2->4 even though they are the same length.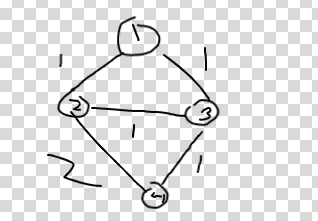 heres my code if it helps https://atcoder.jp/contests/abc243/submissions/30068875
heres my code if it helps https://atcoder.jp/contests/abc243/submissions/30068875
I do not get it.
I tried to do floyd-warshal, and counted edges that can be removed because there exists a shorter path.
But then had to realize that this does not work if there are alternative paths of equal cost. How/Why does this work with your code?
in the triple loop where you calculate distances i check if the intermediate path of i->k,k->j is equal to i->j, because you want floyd warshall to calculate the paths with as many edges as possible. I think this works because you want to use as few edges as possible, so its better to use the already predetermined path rather than new edges that havent been considered yet.
edit: sorry im really bad at explaining things :(
The intuition is that if there are 2 paths with equal cost, we should favor the one that has a greater number of edges because it consists of sub-paths that are themselves shortest paths and already retained from the original graph so this could save us from retaining an edge that we can remove as illustrated by the example omeganot provided. We can maintain the lengths of the paths and favor the "longest" shortest path. Submission
I did Floyd Warshall, but I modified the graph at first. We copy the graph 2 times, so we got 3 Levels of equal graphs. Level $$$1$$$ is our original level, Level $$$2$$$ and Level $$$3$$$ are below Level $$$1$$$. Now I added new Edges. Instead of moving from $$$u_1$$$ to $$$v_1$$$ you are allowed to move from $$$u_1$$$ to $$$v_2$$$ on the second level for the same cost. The same goes for moving from $$$u_2$$$ to $$$v_3$$$. So while moving to a neighbouring edge, you are allowed to go down exactly one level. You are not allowed to go from $$$u_1$$$ to $$$u_2$$$, the same node on a lower level.
Now we do Floyd Warshall. Now for each edge $$$u_1$$$ to $$$v_1$$$ from the original graph, I checked whether the distance from $$$u_1$$$ to $$$v_3$$$ is less or equal to the original distance. If it is less, then obviously we can delete it. If it is the same, then we can also delete it, since we had to use at least 2 edges to go down 2 levels.
My Submission
I used Floyd Warshall to calculate all pair minimum distance,then used the same idea to check if dist[i][k]+dist[k][j]<=dist[i][j] means there is a shorter or equal path present and removed the edge.Finally printed ans/2 as it was counted twice.Sadly finished implementing it 20 mins after the contest. Link
Does it makes sense to put such a question in a beginner round, which even Legends are not able to solve during the contest???
Seems you are new to ABCs lmao, Atcoder Beginner rounds are not for beginners :(
Or maybe their definition of beginners is different but I for sure face difficulties in this beginners contest
In problem E. I used Floyd warshall to find the necessary edges which help to get the minimum distance. then just printed m-important_edges.size().
Got WA on 7 test cases.
Can anyone tell the approach of D Moves on Binary Tree?
i used a stack to precompute only the important moves. Its important to notice that if theres a U following any L or R, its essentially doing nothing. So i just looped through the string and pushed all Ls and Rs into the stack, if theres ever a U and the stack is not empty, pop the top of the stack. The remaining elements will be the only important ones and you will be able to simulate them directly.
You can turn the current number into a binary string.
Can you explain in detail?
After the contest, I realized 'turn the current number into a binary string' is the easiest approach. It is easier than using a stack. Submission
I used a stack during contest though.
didnt think abt binary strings, thats pretty genius lol
one 'U' operation counters one(L/R) operation. lets the operations ar LRLU which is the same as
LR. let's say we are at x position then after 'L' we will be at 2*x but if we do a 'U' operation we will go back to x position. I used an additional vector v; so, you just go in the string from 0 to n-1 and check if s[i]=='U' then v.pop_back() if v is empty just divide x by 2 to go to the parent of x.
after this you will have a vector of L and R in it.
Now,
x is the final answer.
I used the fact that answer is always <=1e18 so whenever our current node goes more than 1e18 we just maintain a count that how much depth we have gone down and no matter what are the moves we will always come back as the answer <= 1e18 Code
Why is this submission for G failing on one test case, I couldn't figure it out https://atcoder.jp/contests/abc243/submissions/30071315
Because of the f*cking sqrt function
Why are you angry? It is well known that it is imprecise, and even if somebody didn't know about it, it makes perfect sense that they learn it in the Beginner contest.
I hate precision
The square root is imprecise for long longs. My square root function fixed your submission: 30080661
Using sqrtl function instead of sqrt Works . Or you can even remove precision error using
ABC is becoming more and more difficult.
Problems A through D are easy, and E through G are reasonable for their score. The only unreasonable problem I see based on the standings is H, which likely was more tedious than actually difficult (judging by the code size of ACs here). Also, it is likely that many people were tricked into thinking about flows after remembering the easier "version" from a recent ABC. Anyway, kenkoooo will soon tell us if there is an objective trend of increasing difficulty (which I don't see).
Upd: E is blue, F and G are yellow. H is the first silver problem in the history of ABC, but other than that nothing unusual. Perhaps the absence of green/cyan problems makes an impression of a big difficulty jump between A-D and E-G, but it already happened in ABC 225 and 227.
where to find the color of a problem?
Here and you can see problems that one user solved or tried but failed.
Thanks
(judging by the code size of ACs here)Is there any way to view other peoples submission?
https://atcoder.jp/contests/abc243/submissions and https://atcoder.jp/contests/abc243/submissions?f.Task=abc243_h&f.LanguageName=&f.Status=AC&f.User= for what I referenced
Indeed ABC is becoming more and more difficult. ABC 242 question C requires DP. In the past, no question Cs required DP. Not that the DP is difficult, but in the past question C used to be easier.
Solved G but couldn't solve E...
How to prove the correctness of Ex?
Ask a noob problem, are there any ways to get the test case for atcoder?
Link
Editorial for F seems too hard to read, Not able to get Why factorials even get in picture ? any one who can help me out here
Disclaimer: I didn't read the editorial.
My solution is
dp[prizes prefix][draws][different prizes]with transitions of the form "draw $$$i$$$-th prize $$$j$$$ times". To find the probability of such transition we have to(i) consider the probability of the prize appearing, which is $$$(w_i/\text{sum }w_i)^j$$$;
(ii) consider the arrangement of the draws (because drawing 1 2 is different from drawing 2 1).
Factorials account for (ii), as there are $$$\text{Binom}(j + l, j) = \frac{(j + l)!}{j! l!}$$$ ways to choose $$$j$$$ positions for the draws that yield $$$i$$$-th prize if there already were $$$l$$$ draws for prizes $$$< i$$$.
Submission link: 30059095
The factorial appears because if you have $$$K$$$ prizes and there are $$$c_i$$$ prizes of each type $$$i$$$, then the number of unique arrangements of these prizes is:
The solution is easier to understand in the language of polynomials. Let us say we have $$$m$$$ distinct prize types, and we want to know the number of ways to arrange $$$k$$$ prizes, such that we have at least one of each of the types. This is $$$k!$$$ times the coefficient of $$$x^k$$$ in the following product:
I think it is clear that the coefficient is the same as the formula for the number of arrangements above. Now let us take probabilities into account. The probability that we will get $$$k$$$ prizes such that we have at least one of each of the types is $$$k!$$$ times the coefficient of $$$x^k$$$ in the following product:
Again it should be possible to convince yourself about this — it's probably most intuitive to think of the coefficient of $$$x^i$$$ as the effect of taking $$$i$$$ of that prize type. With this knowledge, we can solve the problem using DP.
Let $$$dp[i][j]$$$ be a polynomial whose $$$k$$$th coefficient indicates the probability that we have $$$j$$$ distinct types after $$$k$$$ draws (divided by $$$K!$$$), when considering the first $$$i$$$ types of prizes. From this, we get the transition:
With this, we can solve the problem in $$$O(NMK^2)$$$ (or faster with NTT).
I read both two tutorials of problem F, but still find it difficult to understand. Would anyone who solved it share any other hints or ideas please. Thanks a lot.