So here's what I present: a structure for modular arithmetic operations which is short, reusable across static and dynamic moduli, supports 64-bit moduli and is as efficient as performing the operations manually. It requires the C++17 standard or newer.
Motivation
For the most part, there's obviously nothing novel about this idea: it was inspired by other blog posts (63903, 23365), as well as by various submissions to CF problems. On the other hand, I haven't come across a unified implementation like this one, so I believe you may find something of interest in it. I've been using it successfully, and I hope that it can be useful to others as well.
Features
The proposed structure provides the most common arithmetic operations:
- Addition — through the operators
+and+= - Subtraction — through the operators
-and-= - Multiplication — through the operators
*and*= - Division — through the operators
/and/= - Exponentiation — through the
powmethod
It also supports all comparison operations by means of an implicit cast operator. But more importantly, it supports dynamic moduli through a complementary structure (like an add-on).
Preliminaries
In this article I will be using the following aliases for integral types:
using namespace std;
using i64 = int64_t;
using u32 = uint32_t;
using u64 = uint64_t;
using u128 = __uint128_t; // available on 64-bit targets
The Structure
Here it is:
Although it's quite short (24 LOC), there are several things to consider about this structure. Let's investigate them line by line.
Template declaration
template <typename T, auto M> struct Mod {
The first line indicates the template parameters, of which there are two:
T— the type of the wrapped valueM— the modulus (non-type parameter)
T must be an integral type of up to 8 bytes. Its signedness is irrelevant, since we treat it as unsigned internally.
The modulus parameter usually has type T, but may be of any type than can be implicitly converted to it — we'll see how this supports dynamic moduli later on —. For completeness, the following C++20 constraint can be specified:
requires integral<T> && convertible_to<decltype(M), T>
The permissible range for $$$M$$$ is $$$[1,2^{8 \cdot sizeof(T)-1}]$$$. Were it not for the fact that we want to support dynamic moduli, we could add this constraint as well. Alas, the best we can do is append && (sizeof(T) == sizeof(+M)) to the line above.
We declare the structure as a struct so its members are public by default, and deliberately give it a short and memorable name, so it can be used directly (provided that it has default template arguments), making the client code less verbose.
Normally, one would define an alias for a specific combination of template arguments:
using Mint = Mod<int, 1000000007>;
Alternatively, you may assign default template arguments:
template <typename T = u32, auto M = 1000000007> ...
Multiplication type alias
using V = conditional_t<sizeof(T) <= 4, u64, u128>;
This type will be used for holding the result of multiplications and must be at least twice the size of T. Hence, if T is 4 bytes or less, V will be u64; else it will be u128.
We do not care about BigNumber, BigInt or anything of that sort, as these structures generally provide their own mechanism for computing remainders.
Multiplicative inverse
static V inv(V x, V m) { return x > 1 ? m - inv(m % x, x) * m / x : 1; }
This one-liner was borrowed from 23365 (credits to David Wärn). It is a recursive adaptation of the extended Euclidean algorithm which calculates the inverse of $$$x$$$ modulo $$$m$$$, with a time complexity of $$$O(\log^2 m)$$$. Note the use of type V in its definition.
This implementation allows us to compute the modular inverse of any $$$x$$$ coprime with $$$M$$$ (the latter not necessarily prime). It is called by both the division operator and by the exponentiation method (to compute negative powers), but can also serve as a standalone function.
As pointed out by lrvideckis in the comments, an alternative definition for this function would be an iterative one:
static V inv(V x, V m) { // O(log^2 m) | x and m coprime
for (V a = exchange(x, 1), b = exchange(m, 0); b; a = exchange(b, a % b)) {
x = exchange(m, x - (a / b) * m);
}
return x >= m ? x + m : x;
}
Member variable
make_unsigned_t<T> x;
Note that we declare $$$x$$$ as a public member. A more rigorous programmer would make it private, which in the context of a large project would be the correct choice. However, in CP, we will only ever use this for ourselves, so there is no harm in declaring it public (as long as we know what we are doing).
The reason why we interpret T as unsigned is to support values of $$$M$$$ up to $$$2^{8 \cdot sizeof(T)-1}$$$. Some implementations fall short of this limit by a factor of 2, either because they use a signed representation or because their normalization function does not take into account the operation that was performed (addition or subtraction).
We'll see shortly how the normalization can be done to support this requirement. Meanwhile, I invite you to try out this code with your own implementation to see if it works:
Default constructor
Mod() : x(0) {}
The default constructor is called whenever we instantiate the structure without arguments. This happens, for example, when we declare a variable in the stack with no initializer, or resize a vector, or try to access a non-existing map entry.
Since the default value is zero and we don't want to perform the modulo operation in this case, it's better to declare the default constructor separately from the main constructor.
Copy constructor
The copy constructor will be implicitly-declared and defined by the C++ compiler. It is called whenever we instantiate the structure with another Mod instance. This happens when the right-hand operand or value-to-be-assigned is already a Mod instance.
Main constructor
Mod(auto y) : x(y % M) { x >= M ? x += M : x; }
The main constructor is called whenever we instantiate the structure with a plain numeric value. This happens when converting a right-hand operand or assigning a value to an existing Mod instance. It will perform the modulo operation on its argument, store it in the member variable and normalize the result.
The reason why we declare the parameter type as auto is to support integral-valued arguments of any size and sign. Note that in the function body we check if $$$x$$$ is greater or equal to $$$M$$$. This is because $$$x$$$ is unsigned, so any "negative" value will be greater than $$$M$$$, given the constraints on the latter.
There's just one caveat: in order to accept negative arguments, M must be signed. In fact, earlier versions of the code converted it to i64, but this prevented the use of optimized code for dynamic moduli. As we'll see, when the M parameter represents a dynamic modulus it will be a class instance, so casting it would defeat its purpose.
An exception to the above rule is when $$$M$$$ is a power of two (e.g., $$$2^{8 \cdot sizeof(T)-1}$$$), in which case the unsigned modulus works for any $$$y$$$.
Cast operator
operator T() const { return x; }
The cast operator enables implicit conversion of Mods to their wrapped type, which allows them to be compared, passed as parameters to standard functions, etc.. Note that although the type of $$$x$$$ is unsigned, we cast it back to T because this is the "public" type preferred by client code.
It's a matter of personal preference, but I do enjoy being able to work with wrapper structures as transparently as possible. To do this properly, one must be aware of the C++ operator precedence and associativity.
In case you decide not to use this operator, but still want to be able to compare two Mods, you'll have to define the comparison operators explicitly. In C++20 this is simplified by the three-way comparison, which can be declared with a defaulted comparison operator:
auto operator<=>(const Mod &) const = default;
Arithmetic operators
Mod operator-() const { return Mod() -= *this; }
Mod operator+(auto rhs) const { return Mod(*this) += rhs; }
Mod operator-(auto rhs) const { return Mod(*this) -= rhs; }
Mod operator*(auto rhs) const { return Mod(*this) *= rhs; }
Mod operator/(auto rhs) const { return Mod(*this) /= rhs; }
The arithmetic operators are defined in terms of their assignment counterpart. Here we call the default or the copy constructor to create the result value, perform the corresponding assignment operation on it and return it. In theory, the return statement creates another copy, but this should be optimized away by the compiler.
The reason why we declare the parameter type as auto is that we want the right-hand operand to be implicitly converted to a Mod if it is not. Otherwise, we may get error: ambiguous overload for 'operator+' because of our cast operator.
Since the methods are defined entirely inside the structure, they are implicitly inline, i.e., a copy of their function body should be executed without generating the call. Whether they will actually be inlined depends on the compiler or compiler version. For example, here's the annotated assembly of an example program compiled with GCC 13.2. By specifying the -O1 flag, we can see that they do get inlined.
Assignment operators
Mod &operator+=(Mod rhs) { return (x += rhs.x) >= M ? x -= M : x, *this; }
Mod &operator-=(Mod rhs) { return (x -= rhs.x) >= M ? x += M : x, *this; }
Mod &operator*=(Mod rhs) { return x = x * V(rhs.x) % M, *this; }
Mod &operator/=(Mod rhs) { return x = x * inv(rhs.x, M) % M, *this; }
Here's the core functionality of our structure: the assignment operators. They are described below.
Addition: the right-hand operand is added to $$$x$$$ and the result normalized by subtracting $$$M$$$ if necessary, without performing a modulo operation. This works because we're handling two
Modinstances whose values are guaranteed to be within $$$[0,M)$$$, so adding them would yield a value in the range $$$[0,2M-1)$$$.Subtraction: works similarly to addition, except that the right-hand operand is subtracted from $$$x$$$. In this case, the resulting value would be in the range $$$(-M,M)$$$, so it is normalized by adding $$$M$$$ if necessary. For (1) and (2) to work, $$$M$$$ must be within the range $$$[1,2^{8 \cdot sizeof(T)-1}]$$$.
Multiplication: the right-hand operand is first promoted to
V, then multiplied by $$$x$$$ and divided by $$$M$$$ to obtain the remainder. Since both values are non-negative, the remainder will also be non-negative and there's no need to perform normalization.Division: works similarly to multiplication, except that the right-hand operand is first inverted with respect to $$$M$$$. This operator has the same complexity as the inversion function, so it should be used more sparingly than the others.
Exponentiation function
Mod pow(auto y) const { // O(log y) | 0^(-inf,0] -> 1
Mod ans(1), base(*this);
for (auto e = y < 0 ? ~y + u128(1) : +y; e; e >>= 1, base *= base) {
e & 1 ? ans *= base : ans;
}
return y < 0 ? Mod(1) /= ans : ans;
}
The pow method elevates (a copy of) $$$x$$$ to the $$$y$$$-th power using binary exponentiation, returning the result. Both negative and non-negative arguments are supported. In the special case of $$$x$$$ being zero, the result will be 0 if the exponent is positive, or 1 otherwise. It has a time complexity of $$$O(\log y)$$$ (assuming $$$y > 0$$$).
As you may have noticed, the initialization of the for loop uses a special construct to take the absolute value of $$$y$$$.
An alternative definition for this function would be a recursive one:
Mod pow(auto y) const {
return !y ? Mod(1) : y < 0 ? Mod(1) /= pow(-y) : _sqr(pow(y >> 1), y & 1);
}
Mod _sqr(Mod a, bool y) const { return a *= a, y ? a *= *this : a; }
However, it is less readable and less efficient because it produces a function call instead of being inlined.
Dynamic modulus
We finally reach the most anticipated section. In order to support dynamic moduli, we need to define a helper structure that implements the modulo operation in terms of a fast reduction method. For this, we'll be using the Barrett reduction — the reader is encouraged to learn more about this technique before proceeding —.
It can be implemented as follows:
As you can see, it contains the original modulus $$$m$$$ and the precomputed value of $$$\lfloor 2^s/m \rfloor$$$ (where $$$s$$$ is twice the number of bits in $$$m$$$), both of which are used in the Barrett's division and remainder operators to compute the reduction. It supports 32-bit and 64-bit moduli, as well as negative and non-negative arguments.
There are a few more things to note about this structure:
Except for the cast operator, its members are
static. This is because we want to change the value of the modulus at run-time, while still being able to use this structure with ourMod.The cast operator is what allows the
Modto perform value normalization transparently. This will take place in theMod's addition and subtraction operators, as well as in the main constructor.The remainder operator returns the remainder of the division of a signed or unsigned integer by a
Barrettinstance. This will happen in theMod's multiplication and division operators.If the argument's size exceeds that of the precomputed factor, we fall back to the default behavior of the corresponding operator, by relying on C++'s SFINAE.
We can now plug it into our Mod. Just remember to set the modulus before using it:
using Mint = Mod<int, Barrett<int>{}>;
int m; cin >> m;
Barrett<int>::set(m);
Note that Barrett reduction is never used in the Mod's inv method to perform the modulo operation. This is because the modulus changes at each step of the recursion, so it wouln't make sense to apply the reduction in that case.
Making it shorter
We can make the Mod structure shorter by eliminating some of its parts, according to preference and/or need. Here are a few examples:
- the
Vtype alias can be made into an additional template parameter - the
powmethod can be extracted to a derived class or standalone function - if we don't mind using only the assignment operators, the others can be removed
- if neither the
powmethod nor the division operator are needed, then theinvmethod is also not needed
The Barrett structure can also be made shorter:
- the division operator was included for completeness, but is not needed for modular arithmetic
- it can be split in two: one for 32-bit moduli and another for 64-bit moduli, each of them having less code
Pretty-printing in debug sessions
When we debug code that uses Mod instances, we want to be able to see the encapsulated value as if it were the real variable. Of course, this doesn't happen automatically. For example, you might visualize something like this on VS Code:
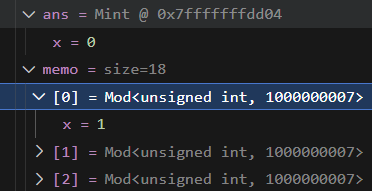
In order to address this issue, we need to customize the debugger. I will now show you how this can be done with LLDB.
LLDB has this concept of type summary, which is a string exhibited next to a frame's variable in the debugger output. You can customize the summary string for a specific type by issuing the following command:
type summary add --summary-string "${var.x}" "<type-name>"
This will display the value of the member variable x as a summary string for any variable of type <type-name>. However, this does not work when the type is enclosed in a container type (such as a vector). In order to make it work with containers, we have to use a regular expression, like so:
type summary add --summary-string "${var.x}" -x "<type-regex>"
Still, if we're not careful with our choice of regex, we might end up with this instead:
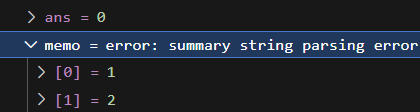
This happens because the regex is matching not only the requested type, but also that of its container. Of course, the summary expression should not be evaluated for the container variable. In our case, what we want is:
type summary add --summary-string "${var.x}" -x "^Mod<"
Notice the anchor character (^) at the start of the regex. This prevents it matching anything that does not start with Mod<. Now it will be displayed correctly:
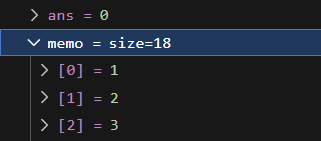
You can use this trick to customize the visualization of other structures as well, such as segment trees, sparse tables, etc.
Depending on your environment, you may be able to configure these commands to run at the beginning of every debug session. If, by some chance, you're using VS Code + CMake, here's the configuration:
For this to work, you'll need to have the LLDB DAP extension installed.
Benchmark
This article wouldn't be complete without a benchmark, so I'm putting here the result of a test adapted from this comment.
| Function | Time |
|---|---|
| run_with_int (static) | 1142.62ms |
| run_with_mod (static) | 691.02ms |
| run_with_mod (dynamic) | 861.67ms |
| Finished in | 2691ms |
As expected, the Mod structure with static modulus performs better compared to the dynamic one. But surprisingly, the latter seems better when compared with the static modulus using plain int.
I believe that the optimization performed by the compiler for constant moduli is similar to a Barrett reduction, in which case the tricks employed by our Mod end up outperforming it. In fact, if we inspect the assembly mentioned previously, produced with the -O1 flag, we'll see this:
This is exactly a reduction, i.e., a modulo operation being replaced with multiplication, division by a power of two and subtraction.
Practice problems
Here's the list of problems to which I have submitted a solution using these structures:
- 1984C2 — Magnitude (Hard Version)
- 1984F — Reconstruction
- 1984H — Tower Capturing
- 1985G — D-Function
- 1992G — Ultra-Meow
- 1996E — Decode
- 2001E1 — Deterministic Heap (Easy Version)
- 2008F — Sakurako's Box
- 2020E — Expected Power
- 2020F — Count Leaves
- 2025B — Binomial Coefficients, Kind Of
Final considerations
That's it! If you end up using these structures, I'd be happy to hear about your findings. Or, in case you encounter any mistakes in this article, please let me know in the comments. Also, if anyone needs help setting up LLDB, feel free to DM me. Thanks for reading!










