Здравствуйте! Пытаюсь сдать задачу "882. Губернатор" с сайта acmp.ru. Недавно я создавал аналогичный пост для другой задачи, под которым подсказали, что в задачах такого рода должен работать жадный алгоритм и нужно лишь определить предикат для сортировки.
В этой же задаче я понял, что ответ не зависит от K и необходимо минимизировать сумму: 
Здесь индексами обозначена последовательность взятия.
Я генерировал маленькие случайные тесты, для которых можно перебрать все n! перестановок и пробовал подобрать предикат, но все безрезультатно. Максимально близко к случайным тестам размера 10 подошел предикат 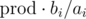 , где
, где 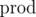 — произведение всех ai. На этом идеи кончились и нужна помощь. Может из-за маленького n решение предполагает динамику за O(n2) времени с памятью O(n), но с ней тоже не вяжется.
— произведение всех ai. На этом идеи кончились и нужна помощь. Может из-за маленького n решение предполагает динамику за O(n2) времени с памятью O(n), но с ней тоже не вяжется.








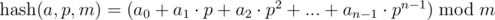
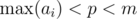 ,
, 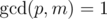 .
. 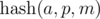 , не взятое по модулю, помещается в целочисленный тип данных (например, 64-битный тип), то можно каждой последовательности сопоставить это число. Тогда сравнение на больше / меньше / равно можно выполнять за
, не взятое по модулю, помещается в целочисленный тип данных (например, 64-битный тип), то можно каждой последовательности сопоставить это число. Тогда сравнение на больше / меньше / равно можно выполнять за 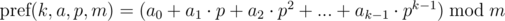
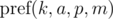 как
как 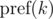 и будем иметь в виду, что итоговое значение берется по модулю
и будем иметь в виду, что итоговое значение берется по модулю 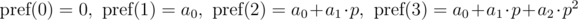
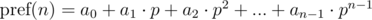
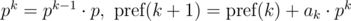
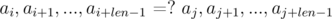
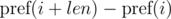 и
и 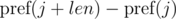 . Не трудно видеть, что:
. Не трудно видеть, что: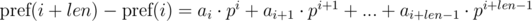
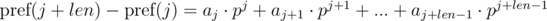
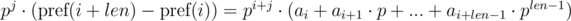
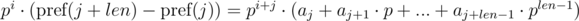
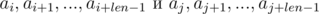
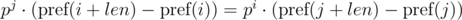
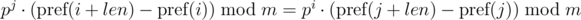
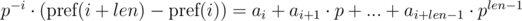
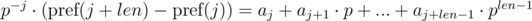
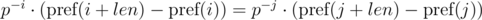
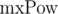 . Домножим 1-е уравнение на
. Домножим 1-е уравнение на 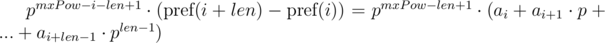
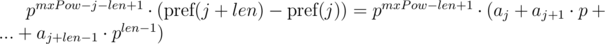
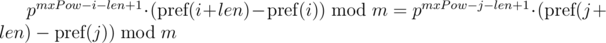
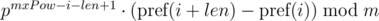 для подстроки длины
для подстроки длины 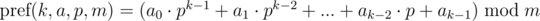
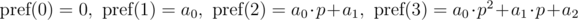
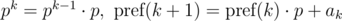
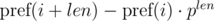 и
и 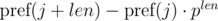 . Не трудно видеть, что:
. Не трудно видеть, что: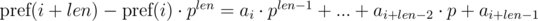
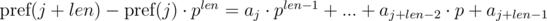
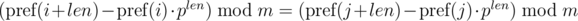
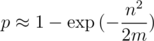
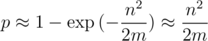
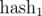 по модулю
по модулю 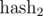 по модулю
по модулю 
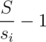 отрезков
отрезков 
