Последнее обновление: решение за O(n) динамическим программированием
Здравствуйте! Задача 736. Удаление с acmp.ru. Суть задачи: на каждой итерации из массива длины n до 5·106 удаляются элементы с индексами k, 2k, 3k и т.д. Затем все неудаленные элементы сдвигаются и операция повторяется до тех пор, пока длина массива не станет меньше k. Нужно для каждого элемента во вводе сообщить, каким по счету он уйдет.
UPD: Решено за O(q * sqrt(n)). Решение Wild_Hamster
UPD2: Так как задача находится в теме "структуры данных", то авторское решение использует некую хитрую структуру данных, которая укладывается и в предел по времени, и в предел по памяти. На это же и намекают лучшие попытки к задаче: там есть решения с 39 МБ и 59 МБ по памяти.
Попробовал сдать код деревом отрезков за O(n log(n)). На acmp.ru — Memory Limit Exceeded (на ideone.com 0.780 с, 84 MB)
UPD3: Написал код деревом Фенвика за O(n log(n)). На acmp.ru — Time Limit Exceeded на 19-м тесте. (на ideone.com 0.480 с, 40 MB).
UPD4: Решение динамическим программированием за O(n): можно решать задачу на префиксе количества итераций, совершенных алгоритмом. Для того, чтобы дать ответ, нам для каждого элемента нужно определить, на какой итерации алгоритма он будет удален, и какому элементу на предыдущей итерации он эквивалентен и использовать уже посчитанный ответ для этого элемента.











Можно фенвиком за NlogN. Запрос "найти минимальную позицию с суммой >= S" выполняется за logN.
Пусть фенвик 1-indexed (так удобнее объяснять и понимать). Пусть p — наибольшая степень двойки, не превышающая N. Тогда в элементе fenwick[p] лежит сумма a[1]+...+a[p]. Сравним ее c S. Если слишком много, повторяем процедуру для массива 1..p, если мало — для массива p+1..N, но уже ищем там S — fenwick[p]. Короче, как бинпоиск, только по степеням двойки, и из-за этого можно сумму не за логарифм считать, а просто в нужный элемент фенвика посмотреть.
Если я правильно Вас понял, то этот подход мне знаком, применял когда-то с деревом отрезков используя подъем и спуск по дереву в задаче с e-olymp: там нужно было выдать минимальный лексикографически отрезок, максимум на котором равен заданному числу. Я уже и забыл, что можно просто использовать свойства структур данных, спасибо.
Я попробовал деревом отрезков, получилось за
O(n log(n)), это работает, но очень много ест и не укладывается в Memory Limit. Код: 0.780 c, 84 MB.А теперь фенвиком попробуй.
https://petr-mitrichev.blogspot.com/2018/02/a-fenwick-bound-week.html
Написал деревом Фенвика за
O(n log(n)): TLE 19 тест на сервере acmp.ru, но памяти теперь ест 40 MB.На acmp.ru в лучших попытках к задаче есть люди, которые сдали с памятью 39 МБ и даже 59 МБ, значит, решение структурами данных все же есть.
Да, можно сдать ДО (и наверное и Фенвика) за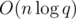
Можно заметить что в вашем решении оно долго работает только тогда, когда k слишком большое. Тогда можно для k <= sqrt(n) использовать ваше решение, а в противном случае рассмотрим, какие значения могут принимать (n - answ) / k и a / k. (n - answ) / k и a / k с каждой итерацией цикла не возрастают, а их начальные значения равны n / k и a / k соответственно. То есть количество возможных изменений в паре значений (n - answ) / k, a / k) будет не больше, чем n / k + a / k. А значит для k > sqrt(n) количество изменений не будет превышать 2·sqrt(n). Тогда мы можем с помощью несложных математических расчетов сделать цикл с не больше чем 2·sqrt(n) операций где в каждой итерации ((n - answ) / k, a / k) будет уменьшаться до ((n - answ) / k - 1, a / k), ((n - answ) / k, a / k - 1) или ((n - answ) / k - 1, a / k - 1).
Я как раз написал свое решение, но Ваше работает быстрее на 0.248. Ниже приведен код. Получается, сложность решения
O(q sqrt(n))?O(q·sqrt(n))
Да, исправил, спасибо. Есть такое ощущение, что эта задача должна решаться легче и заходить не на грани тайм лимита. В тегах к этой задаче на acmp.ru стоит тема "структуры данных", сложность 45%, а если отсортировать все задачи с acmp.ru по сложности (эта задача на 12-й странице расположена), то рядом с ней стоят задачи на сортировку, поиск в ширину, одномерные префикс-суммы, строковые алгоритмы (префикс-функция). Даже без дерева Фенвика, так как, для сравнения, задачи на отрезках начинаются со сложности ~60%.
Пост обновлен, добавлено решение динамическим программированием за линейное время