Submission Хочется рассказать о логике, использованной при решении задачи Е (которую я не успел дописать за отведенное время и засабмитил на дорешивании).
Для этого пригодится знание того, что такое числа Каталана, а также как умение выводить их формулу. Подробно про числа Каталана можно прочитать, например, на вики: тык, Можно по разному дать определение, мы определим число $$$C_n$$$ как количество правильных скобочных последовательностей длины $$$2n.$$$ Нас интересует следующий довольно известный и изящный метод найти это число.
Рассмотрим координатную сетку, по которой нам нужно дойти из угла $$$(0,0)$$$ в угол $$$(n,n)$$$. Мы можем идти только вправо или вверх. Шаг вправо соответствует открывающейся скобке, шаг вверх — закрывающейся. Тогда существует взаимно однозначное соответствие между правильной скобочной последовательностью длины $$$2n$$$ и путем из $$$(0,0)$$$ в $$$(n,n)$$$, не пересекающим диагональ $$$y=x$$$, так как точка выше этой диагонали означала бы что на данном префиксе закрывающихся скобок больше чем открывающихся. Как найти количество таких путей?
Количество всех путей равно $$$\binom{2n}{n}.$$$ Из этого числа мы вычтем количество неправильных путей. Неправильные пути — те, что пересекают $$$y=x$$$, или, что эквивалентно, имеют хотя бы одну общую точку с прямой $$$y=x+1.$$$ Возьмем первую (с наименьшим $$$x$$$) общую точку $$$(a, a+1)$$$ и отразим участок пути от $$$(0,0)$$$ до $$$(a, a+1)$$$ относительно прямой $$$y=x+1.$$$ Получим некоторый путь из $$$(-1,1)$$$ в $$$(n,n)$$$. Это — взаимно однозначное соответствие. Действительно, любой путь из $$$(0,0)$$$ имеющего общие точки с $$$y=x+1$$$ можно отразить до первой такой точки. В то же время любой путь из $$$(-1,1)$$$ в $$$(n,n)$$$ обязан иметь общие точки с $$$y=x+1$$$, так как начало и конец пути расположены по разные стороны от прямой, а значит мы также можем отразить кусок пути до первой такой точки. Количество таких неправильных путей — $$$\binom{2n}{n+1}.$$$ (или. эквивалентно $$$\binom{2n}{n-1}.$$$) А значит количество правильных путей $$$C_n = \binom{2n}{n} - \binom{2n}{n+1}.$$$ Это и есть число Каталана. Подробнее на картинке. 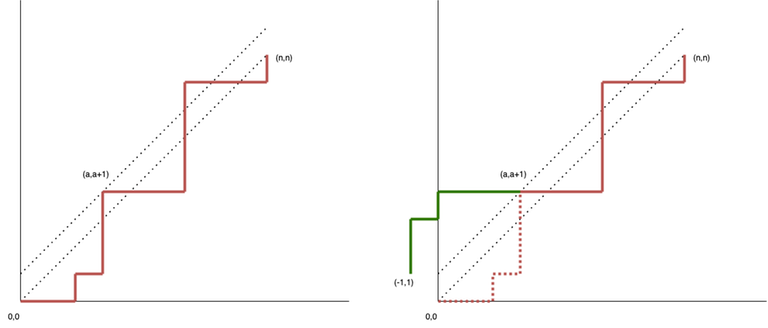
Если бы в задаче не было козырной масти, выигрышное распределение карт между игроками удовлетворяло бы условию что все карты одной масти распределены в порядке правильной скобочной последовательности, по $$$m/2$$$ карт у каждого игрока. Однако наличие козыря потребует от нас двух модификаций для формулу выше.
Во-первых, масть 1 по-прежнему должна удовлетворять условию префикса правильной скобочной последовательности, однако она не обязана быть оконченной. Любой путь из $$$(0,0)$$$ в $$$(a, m-a), a \ge m-a$$$, не пересекающий $$$y=x$$$ удовлетворяет условию. Количество таких путей $$$\binom{m}{a} - \binom{m}{a+1}$$$. Такое распределение мастей оставит нам $$$2a - m$$$ козырей, которые мы можем потратить на дальнейшие масти. Это будет базой нашего ДП. Пусть $$$dp_i[ta]$$$ — количество способов расположить выигрышным образным первые $$$i$$$ мастей, оставив в запасе $$$ta$$$ козырных карт. Тогда $$$dp_1[2a - m] = \binom{m}{a} - \binom{m}{a+1} \forall a \ge m/2.$$$
Во-вторых если мы тратим на масть $$$i \ne 1$$$ $$$k$$$ козырей (это число может быть только четным), это означает что игрок 1 выкладывает $$$(m - k)/2$$$ карт масти $$$i$$$ а игрок 2 — $$$(m+k)/2$$$ карт. При этом карты должны удовлетворять условию "не слишком неправильной" скобочной последовательности, а именно, на любом префиксе количество закрывающихся скобок не должно превышать количество открывающихся больше чем на $$$k.$$$
Соединив эти мысли, получаем что результат — количество путей из $$$(0,0)$$$ в $$$(\frac{m - k}{2}, \frac{m + k}{2})$$$, не пересекающих $$$y = x + k$$$. Плохие пути отражаются аналогичным образом, но относительно прямой $$$y = x + k + 1$$$, в пути стартующие в $$$( -(k+1), (k+1))$$$. Таким образом количество хороших путей $$$f(m,k) = \binom{m}{(m - k)/2} - \binom{m}{(m - k)/2 + k + 1}$$$. 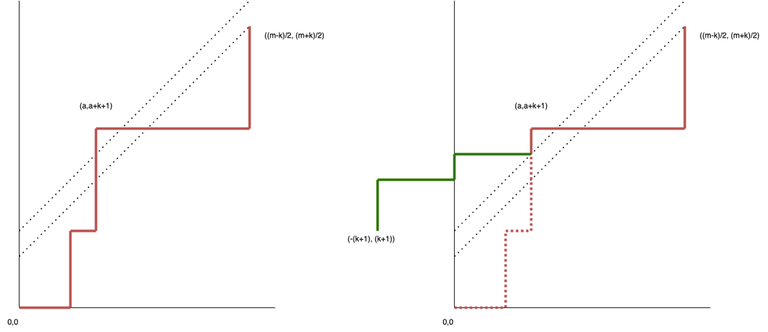
Сам переход ДП несложный: $$$\forall ta \le m, \forall k \le ta, dp_i[ta - k] += f(m,k)*dp_{i-1}[ta].$$$ Достаточно итерироваться только по четным $$$ta$$$ и $$$k$$$. Ответ $$$dp_n[0].$$$ Сложность $$$O(m^2n).$$$