Здравствуй, Codeforces!
Сегодня, 17 октября в 17:35 MSK состоится Codeforces Round #377 для участников второго дивизиона. Участники первого дивизиона, как обычно, смогут участвовать в соревновании вне рейтинга.
Задачи раунда взяты из комплекта задач регионального этапа Всероссийской командной олимпиады школьников, проходившем вчера в Саратове. Комплект задач для онсайта соревнования придумывали и готовили Михаил MikeMirzayanov Мирзаянов, Илья IlyaLos Лось, Данил danilka.pro Сагунов, Владимир vovuh Петров и Роман Roms Глазов. Благодарим многих участников команд Саратовского ГУ за прорешивание соревнования. Одна задача будет присутствовать на раунде в несколько усложненной версии.
С подготовкой задач и переводом к раунду нам помогали Николай KAN Калинин и Татьяна Tatiana_S Семенова — спасибо! Спасибо Михаилу MikeMirzayanov Мирзаянову за системы Codeforces и Polygon.
На раунде вам будут предоставлены 6 задач и 2 с половиной часа на их решение. Желаем удачи!
Если вы участвовали во вчерашнем соревновании в Саратове, пожалуйста, не регистрируйтесь на раунд и не участвуйте в нем, а также не обсуждайте его задачи до окончания раунда.
UPD Разбалловка: 500-1000-1500-2000-2000-2500
UPD2
Поздравляем победителей!
Div.2
Div.1
В связи с ранним временем регистрации на раунд в раунде могут присутствовать несколько участников первого дивизиона, участвовавшие наравне с участниками второго дивизиона. Так как таких не очень много, а исправить эту ошибку представляется технически сложным, все решено оставить как есть.
Так как в Саратове проводится Южный четвертьфинал, пересчет рейтинга будет осуществлен завтра.
UPD3 Разбор









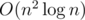 .
.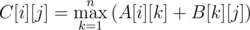
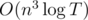 .
. .
.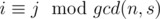 . Будем использовать этот факт и решать задачу для фиксированного
. Будем использовать этот факт и решать задачу для фиксированного 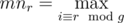 .
.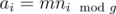 и только из них. Для нахождения количества таких подмассивов будем пользоваться методом двух указателей и для каждого подходящего
и только из них. Для нахождения количества таких подмассивов будем пользоваться методом двух указателей и для каждого подходящего 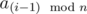 не является подходящим, найдем такое
не является подходящим, найдем такое 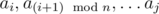 являются подходящими и
являются подходящими и 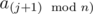 не является подходящим. Пусть
не является подходящим. Пусть 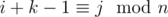 . Любой подотрезок этого подотрезка так же является превосходящим, поэтому к отрезкам длины
. Любой подотрезок этого подотрезка так же является превосходящим, поэтому к отрезкам длины 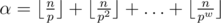 , где
, где 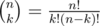 , максимальное
, максимальное 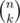 вычисляется по формуле
вычисляется по формуле 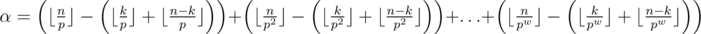 .
.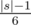 . Будем считать динамическое программирование для каждой вершины
. Будем считать динамическое программирование для каждой вершины 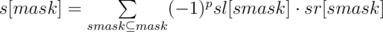 , где
, где 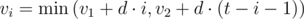 . Действительно, если бы значение
. Действительно, если бы значение  . Это легко объясняется тем, что если существует способ набрать сумму
. Это легко объясняется тем, что если существует способ набрать сумму 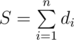 . Зафиксируем очередную кость
. Зафиксируем очередную кость  . Для построения такой последовательности можно воспользоваться следующим жадным алгоритмом: первым числом, очевидно, поставим 0, а среди всех возможных вариантов последующих чисел
. Для построения такой последовательности можно воспользоваться следующим жадным алгоритмом: первым числом, очевидно, поставим 0, а среди всех возможных вариантов последующих чисел  . Общая асимптотика такого решения —
. Общая асимптотика такого решения —  . Решение можно ускорить до линейного, воспользовавшись принципом сжатия путей.
. Решение можно ускорить до линейного, воспользовавшись принципом сжатия путей.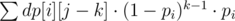 . Простое вычисление такой суммы для каждого состояния займет
. Простое вычисление такой суммы для каждого состояния займет 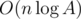 .
.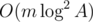 .
.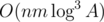 . Можно также заметить, что некоторые ребра лишние, и свести эту оценку к
. Можно также заметить, что некоторые ребра лишние, и свести эту оценку к 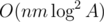 .
.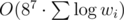
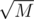 штук (таких блоков, очевидно, тоже
штук (таких блоков, очевидно, тоже 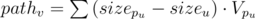 , где
, где 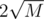 ). Теперь запустим поиск в глубину, который отметит вершины, являющиеся наименьшими общими предками каких-либо двух выделенных вершин. С помощью метода математической индукции нетрудно доказать, что в худшем случае таких вершин будет ровно
). Теперь запустим поиск в глубину, который отметит вершины, являющиеся наименьшими общими предками каких-либо двух выделенных вершин. С помощью метода математической индукции нетрудно доказать, что в худшем случае таких вершин будет ровно 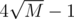 . Таким образом мы получили 'сжатое' дерево, содержащее только необходимые вершины. Предка вершины
. Таким образом мы получили 'сжатое' дерево, содержащее только необходимые вершины. Предка вершины 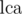 вершины, пунктиром — ребра
вершины, пунктиром — ребра 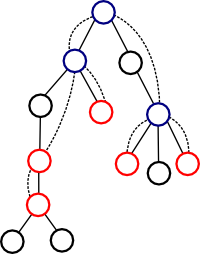
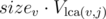 . Теперь мы получили сжатое дерево, в котором все величины посчитаны с учетом того, что поддерево вершины
. Теперь мы получили сжатое дерево, в котором все величины посчитаны с учетом того, что поддерево вершины 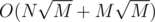 , что в случае
, что в случае 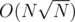 .
. 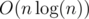 . Однако, этого не требовалось.
. Однако, этого не требовалось.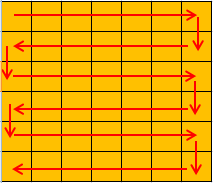
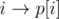 и
и 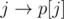 станут ребрами
станут ребрами 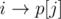 и
и 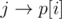 соответственно. Тогда, если
соответственно. Тогда, если 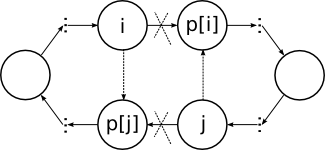
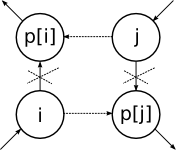
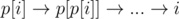 . Поскольку каждый цикл разрывается за линейную сложность, такое решение работает за
. Поскольку каждый цикл разрывается за линейную сложность, такое решение работает за  , можете подумать, как.
, можете подумать, как.
