Hello CF community, I was trying to solve this problem 584B - Kolya and Tanya , I saw that my logic gives wrong answers but I don't know why, my friends' solutions was like find the total cases, subtract the invalid cases but I was thinking of finding the valid cases immediately, here's how I think:
Let's take $$$n=2$$$ for example:
I can either make $$$a_0, a_2, a_4$$$ valid or $$$a_1, a_3, a_5$$$ valid, I know that for every $$$3$$$ vertexes (which are to be valid) I have $$$3^3 - 7 = 20$$$ valid cases, as the invalid cases are:
1. ($$$1, 2, 3$$$)
2. ($$$1, 3, 2$$$)
3. ($$$2, 1, 3$$$)
4. ($$$2, 3, 4$$$)
5. ($$$3, 1, 2$$$)
6. ($$$3, 2, 1$$$)
7. ($$$2, 2, 2$$$)
and for the rest of the vertexes the values I can take are either $$$1, 2,$$$ or $$$3$$$, which means $$$3^{3n-3}$$$ options, so I have $$$n$$$ options ($$$a_0$$$, $$$a_1$$$ in case $$$n=2$$$) with $$$20$$$ valid cases, and for every options of this I have $$$3^{3n-3}$$$ options $$$ \rightarrow $$$ $$$(20\times 3^{3n-3})\cdot n$$$.
Can anyone tell me what's wrong?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
11:08:06
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
11:08:06
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Hello CF community, I'm trying to solve this problem, the problem tells me that I have to calculate
in the numerator it will always be $$$\prod _{i = N-M+1}^{n} i$$$ and in the denominator will be $$$ \prod _{i=1}^{min(N, N-M)}i$$$ as the rest will cancel out
and this is my code: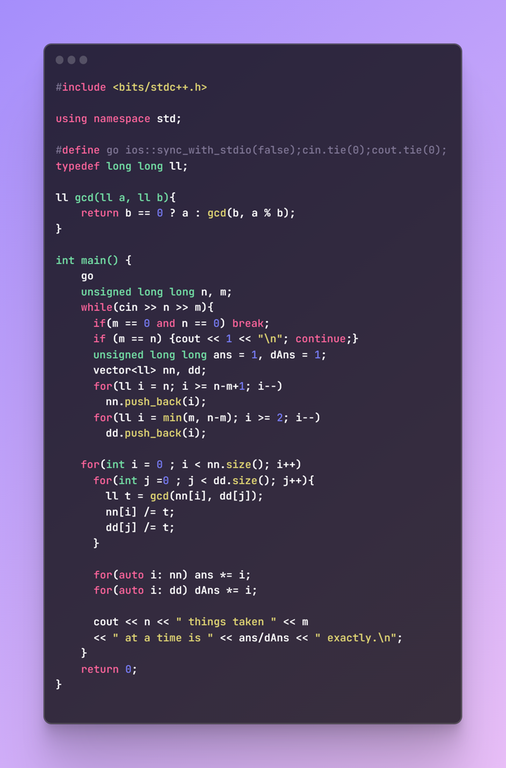
but it gives me WA, I'm not really sure why I'm getting this. Any ideas?
Hello CF community, I'm trying to solve this problem 810B - Summer sell-off, and here's my submission 216849580, Although the code gives AC for the first $$$15$$$ test, it gives a WA on the $$$16$$$-th test, I'm not able to identify the issue, any ideas?. I don't want another solution, I just want to know what's wrong in my solution.
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 06:26:54 (k3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|









