Всем привет!

Осенью на физтехе проходили сборы по программированию Moscow International Workshop ACM ICPC. На них мне довелось прочесть лекцию по суффиксным структурам (на самом деле, были затронуты только суффиксное дерево и суффиксный автомат). В связи с этим я хотел бы предоставить вашему вниманию конспект лекции. Собственно, вот русская и английская версии. Приятного просмотра и счастливого Нового года :)

P.S. любая критика, предложения, пожелания и вопросы всячески приветствуются.

P. P. S. Я попытался достаточно подробно описать доказательство линейности работы, но, скорее всего, оно до сих пор тяжело воспринимается. Вы получите +100 единиц кармы, если разберётесь в нём и предложите более простой для понимания вариант :)

UPD: Спасибо Burunduk1 за помощь в форматировании кода :)

UPD2: См. также статью на Википедии по этой теме. Я являюсь основным автором текущей (29 октября 2021) версии статьи.

Всем привет!

Вообще я думал воздержаться от дальнейших публикаций по палиндромам, так как многие посчитали их слишком навязчивыми. Но задача, о которой пойдёт речь слишком известна и интересна, чтобы не сказать о ней :)

Итак, сама задача: дана строка S. Разбейте её на минимально возможное число палиндромов. Довольно незатейливо, не так ли? Задача довольно популярна. Её можно найти, например, здесь или здесь. Однако, где бы вы её не нашли, ожидаемое решение в лучшем случае будет квадратичным (а то и кубическим). Здесь же будет описано решение этой задачи за в онлайне относительно приписывания символа в конец строки (т.е. ответ будет получен для каждого префикса). Также будет рассмотрена задача разбиения строки на 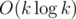k палиндромов и её сведение к разбиению на минимальное число палиндромов.

Можно сказать, что предыдущая часть. Даже если вы считаете, что знакомы с суффиксным деревом, рекомендую просмотреть код внизу.

Всем привет! Наконец, я до него добрался :)

В данной статье я хотел бы избежать длинных и сложных теоретических выкладок, которые долго отпугивали меня от данного алгоритма. Так что сразу к делу. Доказательств приводить не буду, а больше внимания уделю особенностям реализации. Доказательства поищите где-нибудь на stackoverflow (лично я черпал знания об алгоритме именно оттуда) или на wiki-конспектах ИТМО или в книге Гасфилда или в конспекте Юрия Лифшица... Или ещё где-нибудь, где таким любят заниматься.

Всем привет!

Недавно на тренировочных сборах MIPT: The Fall на контесте от Александра Milanin была задача с Petr Mitrichev Contest 7. Суть её заключалась в том, что нам был дан граф и множество запросов вида "допустим, мы удалили из графа k ≤ 4 рёбер. Остался ли он связным?" Я не знаю, какое решение предполагалось автором (буду благодарен, если кто-то расскажет или скажет, где его можно найти, говорят, там что-то красивое :), но далее я хочу рассказать о решении более общей задачи, когда рёбра произвольно добавляются и удаляются, за в оффлайне. Первый алгоритм с такой оценкой был получен Дэвидом Эппштейном в 1992 году сведением к fully dynamic minimum spanning tree problem, однако здесь речь пойдёт о более простом алгоритме, предложенном в 2012 году Сергеем Burunduk1 Копелиовичем.

Всем привет!

В этот раз я хотел бы написать про алгоритм Ахо-Корасик. Структура эта очень хорошо описана и многие о ней уже, должно быть, знают. Однако, я всё же постараюсь описать некоторые применения, которые не столь известны.

Всем привет!

Как некоторые уже знают, на этих летних сборах в Петрозаводске droptable презентовал новую структуру данных, а именно дерево палиндромов. Я имел честь поучаствовать в изучении структуры за полгода до этого, о чём и хочу теперь рассказать :)

Всем привет!

Сегодня начались летние петрозаводские сборы. Надеюсь, не нарушу никаких негласных запретов, написав о них :)

Если вы, как и я, входите в группу людей, которые не имеют возможности участвовать в этом празднике жизни, можете следить за ходом сборов и "болеть" за любимые команды, например, на SnarkNews или на acm.math.spbu.ru.

Всем привет!

Некоторые из вас могут помнить мою статью про policy based data structures. Кроме обзорной статьи на эти структуры, я также хотел написать про возможность использования самописного Node_Update в структуре. Тогда мне так и не удалось выделить на это достаточно времени, однако теперь я могу и хочу наверстать упущенное и поделиться с вами новыми знаниями.

Всем привет!

Недавно на хабрахабре была опубликована статья про такую структуру данных, как списки с пропусками. Как мне показалось, структура весьма интересна и при этом проста в использовании. Именно поэтому сейчас я решил поэкспериментировать со структурой на различных задачах и попробовать реализовать над ней различные модификации.

Всем привет!

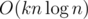Буду краток. Возможно ли искать число K-инверсий быстрее, чем за ? Если да, то как? Если нет, то почему?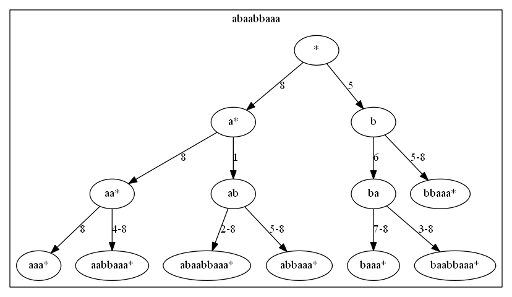

Всем привет!

Ни для кого не секрет, что в спортивном программировании достаточно часто приходится работать с графами^{[источник?]}. Зачастую нам для наглядности приходится эти графы ещё и рисовать. И, возможно, некоторые пользователи уже знают, что с этим делом необычайно хорошо справляется пакет утилит для визуализации графов GraphViz, который парсит код с уже упомянутого мной языка DOT в наглядную картинку с соответствующим графом.

Пример графа, который можно получить с помощью graphviz — сжатое суффиксное дерево для строки abaabbaaa. Да, граф содержит небольшую ошибку, но это не главное :)

Теперь, собственно, к теме. Как вы относитесь к тому, чтобы поддержка языка DOT была добавлена в редактор codeforces? Лично я считаю, что это было бы круто, а вы? :)

P.S. Полезные ссылки по теме:

• Статья, в которой описываются основные методы языка DOT, с примерами
• canviz — библиотека на javascript для рендера графов с языка DOT

Всем привет! Недавно меня заинтересовала такая задача: дано дерево с корнем в вершине 0. Поступают запросы двух видов.

1. Добавить к вершине k сына.
2. Выдать номер предка вершины k, у которого высота равна h.

Вершины пронумерованы в порядке добавления.

Пока что я знаю только два метода решения:

1. Двоичный подъём. Ну тут всё очевидно, времени и памяти.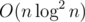
2. С помощью индексированного двоичного дерева поиска (например, неявная дерамида) поддерживаем эйлеров обход графа. Далее либо сводим к k-ой порядковой статистике на префиксе, либо храним для каждой высоты список вершин и находим нужную бинарным поиском. Это потребует O(n) памяти, но времени (возможно, при грамотной реализации можно и , но я точно не знаю), ещё и с большущей константой.

Интересно то, что оба метода подозрительно похожи на LCA. В связи с этим возникает вопрос — может, задачу можно как-то свести к LCA непосредственно? Ну и, конечно, интересно, какие ещё есть способы решения этой задачи, в том числе и в оффлайне.

Всем привет! 2 года назад Logvinov_Leon поинтересовался у сообщества о существовании способа перевести суффиксный автомат в суффиксный массив. Ответа, как ни странно, он не получил. Но, так как я, как вы, возможно, заметили, люблю переводить одни строковые структуры в другие, я решил эту тему добить.

И снова всем привет! Недавно, решая задачу 1937 с Timus'a (кстати, и вам советую! Отличная возможность отточить умения в строковых алгоритмах сразу в нескольких направлениях), я столкнулся с необходимостью нахождения всех подпалиндромов в строке. Опытные программисты уже знают, что одним из лучших алгоритмов для этого является алгоритм Манакера, позволяющий получить все подпалиндромы в сжатом виде без каких-либо дополнительных структур. Единственная проблема — алгоритм сравнительно сложен в реализации. То есть, его идея проста и понятна, а вот реализации обычно оказываются нагромождениями кода с повсеместным рассмотрением того, где написать +1, а где -1.

Всем привет! Осталось меньше суток до начала раунда 1B. Если вы, как и я, предпочли сон замечательному раунду 1А, то этот раунд именно для вас! 1000 участников, показавших лучший результат пройдут во второй раунд и не будут иметь возможности поучаствовать в следующем подраунде.

Напоминаю, что раунд пройдёт в субботу, 3 мая в 16:00 UTC на сайте, который и так все знают.

Всем привет! Меня всегда завораживало то, как хитро сплетены так называемые "строковые алгоритмы". Полгода назад я писал здесь статью о возможности быстрого перехода от Z-функции к префикс-функции и обратно. Некоторые опытные пользователи уже знают, что такие переходы возможны и между более сложными строковыми структурами — суффиксным деревом и суффиксным автоматом. Такой переход достаточно подробно описан на е-maxx.ru. Сейчас же я хотел бы в целом рассказать о такой структуре, как суффиксное дерево, а также поделиться достаточно простым (с теоретической точки зрения) способом его быстрого построения — получением суффиксного дерева из суффиксного массива.

Всем привет! Думаю, многие знают про такой тип данных, как множество. Он должен поддерживать следующие операции:

• Добавить элемент в множество;
• Узнать, есть ли элемент в множестве;
• Удалить элемент из множества.

Если речь идёт о множестве упорядоченном, то элементы также должны располагаться в нём в определённом порядке. Лично я считаю, что для упорядоченных множеств также очень важны следующие операции:

• Узнать, какой элемент является K-ым в множестве;
• Узнать, какой номер был бы у элемента, если бы он находился в этом множестве.

Чаще всего для реализации такого функционала используются двоичные сбалансированные деревья (AVL-дерево, красно-чёрное дерево, декартого дерево, etc). Однако в этой статье я бы хотел поговорить о некоторых особенностях в реализации упорядоченного множества на других структурах. В частности, в этой статье мною будут рассмотрены реализации на дереве Фенвика и на дереве отрезков. Сразу хочу отметить, что это позволяет воссоздать множество только над множеством натуральных чисел. Для любых прочих типов элементов в множестве такие методы не сработают :(

Основная идея такой схемы заключается в следующем:

Пускай индекс элемента в массиве (назовём его для удобства arr), над которым мы строим наше множество, будет соответствовать его значению, а значение — количеству таких элементов в множестве. Тогда легко заметить, что мы сможем выполнять все требуемые операции за время не хуже, чем логарифм, т.к. добавление элемента x в множество будет соответствовать инкрементированию ячейки arr[x] (или присвоению единицы, если множество уникальное), проверка элемента на наличие в множестве — это получение значения ячейки arr[x] (в дереве Фенвика не прокатит, там, судя по всему, прийдётся вычислить sum(x, x)), удаление элемента — декрементирование ячейки (присвоение 0, если множество уникальное), номер элемента в множестве — это sum(0, r - 1). Отдельно стоит отметить операцию нахождения K-ого элемента. Для этого прийдётся использовать технику двоичного подъёма. В дереве отрезков для этого потребуется поддерживать размеры поддеревьев, как в BST, а в дереве Фенвика мы можем, внимательно рассмотрев следующее изображение, показывающее принцип распределения элементов по частичным суммам, вывести такой алгоритм:

    int get(int x)
    {
        int sum=0;
        int ret=0; // Номер первого элемента в массиве, сумма в котором равна текущей
        for(int i=1<<MPOW;i && ret+(i-1)<N;i>>=1) // Перебираем степени двойки, начиная с максимально возможной
        {
            if(sum+arr[ret+(i-1)]<x) // Учитывая, что функция суммы монотонна, стараемся расширить текущий префикс
                sum+=arr[ret+(i-1)],
                ret+=i;
        }
        return ret;
    }

Легко заметить, что при таком подходе ret всегда имеет такое значение, что в следующий раз какое-то число из отрезка [0;ret] встретится не ранее, чем в точке ret+i, однако, в силу постояннного убывания i, мы никогда не достигнем такой точки, а значит, ни один элемент в префиксе не будет учтён дважды. Это даёт нам право полагать, что алгоритм правильный. И проверка на некоторых задачах это подтверждает :)

Основная идея изложена, теперь поговорим о достоинствах и недостатках такого подхода.

Достоинства:

• Быстро пишется;
• Интуитивно понятно (особенно, в случае с деревом отрезков);
• Быстро работает (на практике чаще всего обгоняет BST);

Недостатки:

• Ограниченная функциональность (поддерживает только натуральные числа в множестве);
• В самом простом виде занимает O(C) памяти, где C — максимальное возможное число в множестве;

Второй недостаток ОЧЕНЬ существенный. К счастью, его можно устранить. Сделать это можно двумя способами.

1. Сжатие координат. Если мы можем решать задачу в оффлайне, то мы считываем все запросы и узнаём все возможные индексы, к которым нам прийдётся обращаться. Сортируем их и ассоциируем с наименьшим из чисел единицу, со вторым — двойку и т.д. Это позволяет снизить расход памяти до O(M), где M — количество запросов. Однако, к сожалению, это не всегда работает.
2. Динамическое расширение дерева. Способ заключается в том, чтобы не хранить вершины в дереве, которые нам не нужны. Есть, как минимум, три способа. К сожалению, для дерева Фенвика подходит только один из них. Первый вариант — использовать хеш-мапы. Плохой, очень плохой вариант. Точнее, с ассимптотической точки зрения он хороший, но хеш-мапы обладают очень большими константами, поэтому я не рекомендую этот метод. К сожалению, именно он — тот единственный, что доступен для дерева Фенвика :). Второй — расширение указателями. Когда нам в дереве нужна новая вершина, мы просто создаём её. Дёшево и сердито. Однако, это всё ещё не самый быстрый вариант. Третий — статически выделить блок в MlogC вершин, после чего для каждой вершины хранить индексы её сыновей (как в боре). На практике именно этот способ оказывается наиболее быстрым. Расход памяти же во всех трёх способах снижается до O(MlogC), что уже, в целом, приемлемо.

Вновь надеюсь, что был интересен/полезен кому-нибудь. До новых встреч :)

Всем привет! Недавно на, думаю, известном многим вам ресурсе habrahabr.ru была выложена статья про структуру данных, именуемую link-cut tree. Это первая известная мне русскоязычная статья на эту тему, ни на e-maxx'e, ни на вики-конспектах ИТМО, насколько мне известно, эта структура не описана, поэтому, считаю уместным сообщить о статье здесь.

Итак, собственно, статья.

Всем привет! Многие видели статью пользователя Zlobober, в которой говорилось о том, что строка Туэ-Морса с ужасающей силой валит хеши по модулю 2^64. Одиночные же хэши оказались слишком небезопасными из-за парадокса Дней Рождения. Единственное оставшееся спасение от инфернальных суффиксных структур было двойное хэширование. Однако, скоро и ему прийдёт конец. Основательно изучив строку Туэ-Морса и её возможные модификации, я пришёл к выводу, что тест, ломающий даже решения с двойным хэшем возможен.

Здесь я подробнее описал построение теста, его использование против реальных решений с различных контестов и обоснование его работы.

Теперь же предлагаю пользователям codeforces обсудить, что следует делать в сложившейся ситуации. Неужели больше совсем не осталось способов решать задачи полиномиальными хэшами? У кого какие мысли по этому поводу?

Всем привет! После достаточно долгого затишья, я решил, что мой вклад растёт слишком медленно пришёл час порадовать вас ещё одной статьёй в блоге :)

2 месяца назад пользователь Perlik выложил статью, в которой описал очень интересную реализованную в STL структуру, которая позволяла очень быстро производить различные операции с подстроками. Некоторое время после этого я тестировал её на различных задачах и, к сожалению, как правило, получал негативный результат — rope оказалась слишком уж медленной, особенно когда речь шла о работе с отдельно взятыми элементами.

На некоторое время я позабыл о той статье. Однако всё чаще я сталкивался с задачами, в которых нужно было реализовать множество, да не простое, а золотое с возможностью узнавать порядковый номер элемента и, напротив, элемент по его порядковому номеру (т.е., порядковую статистику в множестве). Вопрос выполнения этих операций методами стандартной библиотеки достаточно тонкий и актуальный, подтверждением тому можно привести, например, этот и этот блоги. И тут я вспомнил о том, что в комментариях к той статье кто-то упомянул о загадочной структуре данных order statistics tree, которое как раз поддерживает эти две операции и которое как раз реализовано в STL (хотя и только для GNU C++). Тут и началось моё увлекательное знакомство со структурами данных, основанными на политике (policy based data structures), о которых я хочу поведать и вам :)

Серьёзно, всё ещё никто не написал об этом? Ну ладно. С Новым Годом, народ! Желаю всем в этом году новых свершений в олимпиадном программировании, высокого рейтинга на Codeforces, TopCoder и где он ещё вам может понадобиться, бескнонечно весёлого настроения и, конечно, здоровья и счастья и пусть все ваши мечты сбудутся =)

BTW, в Украине Новый Год наступил всего-навсего 10 минут назад =)

Всем доброго времени суток!

Сегодня мне захотелось написать статью о таких зачастую важных на олимпиадах элементах STL, как map и set, то есть, о множествах. Понимаю, что практически все участники div. 1, которые пишут на С++ с ними знакомы и для них статья будет малополезной. Однако, как мне кажется, многие участники div. 2 напротив, могут о них не знать. В первую очередь на них и ориентирована данная статья. Также хочу отметить, что буду рад всякой критике, если Вы сочтёте её необходимой.

Всем доброго времени суток!

Изучая столь часто применяемые к строкам Z- и префикс-функции, я задумался, а можно ли быстро (за О(n) ) переходить от одной к другой? По крайней мере, на e-maxx этого не было описано и я решил провести такой мини-анализ самостоятельно.

Всем доброго времени суток!

Начался отборочный (заочный) этап олимпиады, который продлится до 15 января. Опубликованы первые пять задач олимпиады (новые задачи будут добавлены позже), открыта регистрация и тестирующая система для сдачи задач. Весной 2014 года будет проведен очный финальный тур олимпиады, на который будут приглашены участники, показавшие высокие результаты в заочных турах. Страничка олимпиады — olympiads.ru/zaoch.