Сегодня вечером в 20:00 по Москве состоится SRM #608.
К слову, в это же время начинается церемония открытия зимней олимпиады в Сочи и её прямая трансляция.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Сегодня вечером в 20:00 по Москве состоится SRM #608.
К слову, в это же время начинается церемония открытия зимней олимпиады в Сочи и её прямая трансляция.
До раунда 15 минут, а анонса всё нет. Не пропустите!
Кажется, все, кому актуально, и так должны знать, но всё же напомню.
Сегодня в час ночи по Москве состоится третий раунд Facebook Hacker Cup. Топ-25 кулхацкеров выходят в финал.
Сегодня в 19:00 по Москве состоится Test SRM.
Что означает Test SRM? Он же все равно рейтинговый, правда?
Через полчаса (в 19:00 по Москве) состоится SRM #577.
Предлагаю обсудить задачи здесь по окончанию.
Всем привет!
Начался заочный этап VII Открытой олимпиады школьников по программированию! Он продлится ориентировочно до середины января 2013 года. В марте 2013 состоится финальный этап олимпиады, на который будут приглашены около трёхсот лучших школьников по итогам заочного этапа.
В течение трёх месяцев будет предложено около десяти-двенадцати задач. Они будут появляться порциями на сайте олимпиады. Вы найдёте задачи различного уровня сложности, как для только начинающих изучать основы программирования, так и для профессионалов, уже достигших успехов на опимпиадах выского уровня.
В этом соревновании ежегодно принимают участие школьники разных стран. Допускается участие вне конкурса всех желающих, не только школьников.
(05.11.12) UPD1: Добавлены задачи E — G.
(06.11.12) UPD2: Напоминаем, что данный пост также не является местом для какого-либо обсуждения содержательной части задач. Все вопросы задавайте жюри в тестирующую систему.
(15.11.12) UPD3: Произошёл реджадж по задаче C. Результаты могли измениться не в лучшую сторону :-)
(12.12.12) UPD4: Красивая дата. Тем временем постепенно были добавлены последние шесть задач. Обратите внимание: изменилось условие задачи L.
(19.12.12) UPD5: Сервер временно недоступен. В течение суток всё должно подняться.
(19.12.12) UPD6: Всё починилось.
(29.12.12) UPD7: Задача M была перетестирована. Обратите внимание, изменился порядок тестов и на некоторых тестах результаты ваших программ могли ухудшиться.
(05.01.13) UPD8: Как вы многие заметили, ночью прошёл полный реджадж всех посылок, который производился с целью тестирования возможностей новой версии ejudge. Также был удалён некорректный тест по задаче L. Результаты могли улучшиться :-)
(10.01.13) UPD9: Традиционным образом жюри олимпиады приняло решение продлить заочный тур аж до 23:59 26 января!
Принимайте участие и приглашайте всех знакомых :-)
Hello!
Does anyone have test data for BOI 2012? Links on official site are broken :-(
Also I didn't find any contacts there. Maybe somebody has e-mail, or any contact of jury of that olympiad?
UPD: there can be some type of misunderstanding. I mean Baltic Olympiad in Informatics, not Balkan.
Всем привет. Хочу поделиться с общественностью некоторым фактом, который позволяет ломать с гарантией почти любое решение, использующее полиномиальные хэши от строк, где в качестве модуля используется 264 тестом длины порядка нескольких тысяч. Причём, не важно, какое число берётся за точку в полиноме, важно лишь, что все вычисления производятся в типе int64 со стандартными переполнениями — а так пишут большинство олимпиадников.
Для привлечения внимания ключевые слова: не пишите, как написано у е-макса! И только сегодня, только для вас — ломаем решение Petr на задаче 7D - Палиндромность с Codeforces Beta Round #7!
Интересно? Прошу под кат.
Сейчас в Венгрии начинается CEOI 2012 — центральноевропейская олимпиада школьников по информатике. Олимпиада — очень интересная, задачки — крутые, непростые по школьным меркам. По этим же задачам будет проведена интернет-траснляция: первый тур — 09.07.12, второй — 11.07.12, оба тура будут идти с 12:00 до 17:00 по Москве.
Правила — старый IOI, с группировкой по тестам (баллы за группу начисляются только по прохождении всех тестов).
Регистрация закрывается завтра (08.07.12) в 22:00 по Москве!
Го участвовать?
UPD: (possibly) rules changed this year.
UPD2: you should have recieved e-mail wih password and instructions. Rules indeed were updated.
UPD3: Contest server is veeeery slow so here is the mirror for the tasks (thx to popoffka)
UPD4: Here is mirror for second day statements (thx to yeputons):
Делал тут для себя шпаргалку по хэштейблам в новой версии стандарта C++, и мне подумалось: а почему бы со всеми не поделиться?
Вообще в C++11 в STL появилось некоторое количество новых плюшек, большинство из которых вряд ли пригодятся программистам-олимпиадникам. Красивую схемку с их описанием можно найти здесь. Но две новых структуры данных, которые наконец были включены в стандарт, заслуживают внимания — это unordered_set и unordered_map.
Многие, наверное, знают, что из себя представляет хэш-тейбл. Это контейнер, позволяющий добавлять, удалять и искать элементы за O(1) в среднем. Принципиально бывают хэштейблы с цепочечной (не знаю, насколько принят в русскоязычной литературе такой термин?) и открытой адресацией. Вкратце напомню разницу.
В цепочечном варианте хэштейбл для каждого значения хэша хранит все элементы с таким хэшом в виде списка (под словом список следует понимать либо list, либо динамически расширяющийся массив, либо что-нибудь ещё такое, по чему можно тупо проитерироваться). Тем самым, в самом хэштейбле значения непосредственно не хранятся — хранятся лишь линки на контейнеры с ними, называемые также по-английски bucket'ами. Как правильно переводится такой термин на русский, кстати?
В варианте с открытой адресацией, в отличие от цепочечного хранения, значения хранятся непосредственно в самой таблице, однако не гарантируется, что элемент X гарантированно будет лежать в ячейке с номером Hash(X). На самом деле, обычно bucket'ы из предыдущего варианта просто укладываются сверху вних в самой таблице — то есть, если мы не нашли нужное нам значение в ячейке Hash(X), посмотрим в ячейку Hash(X) + 1, потом в Hash(X) + 2 и так далее. Возникает проблема, что если из ячейки 424243 растёт bucket размера 5, а из ячейки 424245 — bucket размера 6, они обязательно перекроются. Но на это мы забьём — нам просто придётся пройтись по всем значениям — в том числе и принадлежащим к чужому bucket'у — когда понадобится дойти до нужного в операции поиска.
STL реализует первый вариант хэш-таблицы. Идейно unordered_set реализует все те же самые методы и свойства, что и обычный set, то есть в первом приближении им можно точно так же пользоваться:
#include <unordered_set>
#include <iostream>
using namespace std;
int main()
{
unordered_set<int> S;
int n, m, t;
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> t;
S.insert(t);
}
cin >> m;
for (int i = 0; i < m; i++)
{
cin >> t;
if (S.find(t) != S.end())
cout << "YES" << endl;
else
cout << "NO" << endl;
}
return 0;
}
Разберём поподробнее все интересные методы и свойства. Какие есть шаблонные параметры у класса.
template<
class Key,
class Hash = std::hash<Key>,
class KeyEqual = std::equal_to<Key>,
class Allocator = std::allocator<Key>
> class unordered_set;
Первый параметр — единственный обязательный — это собственно тип того, что мы будем хранить.
Второй параметр — это хэш-функция. Это должен быть объект (структура или функция), у которой оператор (), выполненный от объекта типа Key, возвращает величину типа size_t, равную хэшу объекта. По умолчанию хэшером является std::hash — этот класс умеет хэшировать все стандартные числовые типы, стринги, битсеты и ещё пару C++-ных типов (здесь подробнее). Можно в качестве этого параметра написать свою структуру, а можно перегрузить std::hash под свой тип Key. Рекомендую пользоваться вторым способом — он идейно проще. Пример приведён ниже.
namespace std {
template<>
class hash<S> {
public:
size_t operator()(const S &s) const
{
size_t h1 = std::hash<std::string>()(s.first_name);
size_t h2 = std::hash<std::string>()(s.last_name);
return h1 ^ ( h2 << 1 );
}
};
}
Третий параметр — это функция сравнения. Так как в одном bucket'е все значения лежат вперемешку, структура должна как-то уметь проверять — очередное значение это то, что надо, или нет? По умолчанию это std::equal_to, который просто вызывает оператор ==, который стоит перегрузить для ваших типов.
Четвёртый параметр — это стандартный для всех STL'ных структур аллокатор. Про него ничего говорить не буду — его лучше отдельно не касаться, кому интересно — сами прочитаете :-)
Интересно, что в отличие от многих других STL'ных структур unordered_set даёт доступ к тому, как он реально устроен. То есть у него есть интерфесы для работы непосредственно с bucket'ами. Каждый bucket идентифицируется своим номером с нуля. Для очередного объекта номер bucket'а, куда он попадёт, вычисляется как Hash(x) % bucket_count(). Но более кошерно использовать метод bucket(Key), который вернёт номер bucket'а, куда попадёт ключ Key.
У хэштейбла есть такой параметр, как bucket_count() — он возвращает текущее количество bucket'ов. Верно следующее: автоматически происходит тотальный рехэш, когда количество элементов в хэш-таблице превзойдёт max_load_factor() * bucket_count(). Что это значит? max_load_factor() — это просто константа для хэш-таблицы, которая указывает пороговое значение среднего количества элементов на bucket для тотального рехэша. Поправить это значение, можно вызвав max_load_factor(f), это установит max_load_factor равным f. f должно иметь тип float.
Итераторы у хэш-тейбла проходят сначала по очереди по всем bucket'ам с нулевого по (bucket_count() - 1)-ый. Методы begin() и end() работают как обычно, но им можно передать параметр t, который даст итераторы на начало и конец t-ого bucket'а.
Есть интересный метод emplace(Args&&... args). Он вставляет в хэштаблицу значение, но не как обычный insert, которому надо готовое значение отдать, а он с помощью конструктора копирования его вставит. emplace же в нужном месте просто вызовет конструктор копирования (которому, например, для стрингов достаточно просто скопировать ссылки на расположение строки в памяти за O(1)).
Итераторы инвалидируются с каждой операцией перехэширования, которое происходит автоматически при достижени порогового фактора загрузки, либо которые можно вызвать методами reserve(n) (зарезервировать места под n элементов), либо rehash(n) (зарезервировать места под n bucket'ов).
Вот пожалуй и всё. Ещё бывает unordered_multiset, который отличается возможностью хранения нескольких идентичных ключей. Ещё бывают unordered_map и unordered_multimap, которые отличаются от unordered_set ровно тем же, чем map и multimap отличаются от set.
Полезная, в общем, структура. Но в отличие от set, который обгоняет большинство рукописных сбалансированных деревьев поиска, хэштаблица, во всяком случае в g++ 4.6.1, сделана так, чтобы применяться во всех мыслимых и немыслимых ситуациях, и это происходит в ущерб скорости. То есть естественно, что рукописная хэш-таблица с открытой адресацией, содержащая int'ы с хэшированием по модулю 2^16, делает STL'ную раза в три по скорости.
Думаю, такая шпаргалка кому-то окажется полезной — я не из тех, кто сильно любит писать структуры данных руками, был рад появлению хэштаблицы в C++11 :-)
Всем привет. Я для себя некоторое время назад написал простой юзерскриптик, который подсвечивает уже просмотренные посылки в табличках.

Паша Кунявский предложил поделиться со всеми.
В силу того, что нехорошо нагружать сервер дополнительными AJAX-запросами, функциональность, которую можно выдернуть из загруженной страницы очень небольшая. Просмотром посылки считается открытие ячейки с ней в таблице. Посылки хэшируются как (юзер, задача, время), поэтому сабмиты в течение одной минуты от одного пользователя по одной задаче посчитаются одинаковыми, ну да невелика потеря :-)
Если кто несогласен с моим внутренним чувством стиля, всегда можно подредактировать скриптик, а именно функцию color, поставив собственное правило отображения.
Скрипт работает в Firefox в Greasemonkey, в Chrome по умолчанию есть поддержка скриптов, про оперу, честно говоря, не знаю.
Могу чего-нибудь поправить. Пользуйтесь на здоровье!
Оно работает как во время текущих контестов, так и в прошедших — можете сегодня потестировать.
UPD1: теперь работает и по дабл-клику, и по ctrl-клику.
UPD2: теперь работает и в Opera.
Скажите, добавить фичу авто-обновления страницы? Или все её решают сторонними плагинами?
Однако лето наступило! И я хочу напомнить о таком замечательном летнем мероприятии как Internet Problem Solving Contest или IPSC. Это очень интересный интернет-контест, в котором допускается участие как в командном, так и в личном зачёте, причём школьники могут идти также в отдельном зачёте.
Среди задачи преобладают обычные output-only алгоритмические задачки, но наравне с ними встречаются мягко говоря необычные. Например, в прошлом году одна из задач была натуральным тамогочи — за правильные ответы из штрафного времени вычиталось по 20 минут, с неправильным ответом питомец помирал/убегал :-)
Сегодня, 1 июня, с 12:00 по Москве стартанёт пробный тур, который будет продолжаться сутки. Рекомендуется всем, кто не знаком с системой его написать — там тоже есть интересные и необычные задачи
Основной тур — 2 июня с 14:00 по Москве. Участвуйте, это интересно!
Наши команды:
SPbSU4 (Dmitry_Egorov, PavelKunyavskiy, yeputons)
Endeavour to Jump Together (tatyanakov, Goshish, Malinovsky239)
Ide (yarrr, caustique, ant.ermilov)
unusual (eduardische, nvilcins, gen)
Ponyville Coders (ivan.popelyshev, halyavin, iroro)
Unacceptable Solutions Inc (cmd, mastersobg, cheshire_cat)
krasprog unpredictable (oversolver, kormyshov)
Индивидуальные участники: Scorpy (Scorpy), Gerald (Gerald), homo_sapiens (Edvard), grey_wind (grey_wind)
UPD: Доступны решения.
Сегодня в 18:00 по Москве состоится GCJ Round 2. Напоминаю, что это шанс получить крутую футболочку — входите в число лучших 1000 участников и она ваша. 500 лучших участников проходят в Round 3.
Ололо.
Линк.
Я что-то пропустил? Это такой глюк? Или флешмоб организовался? :-)
Я не видел пока ни одно комментария рейтингом выше нескольких сотен, а тут аж две тысячи.
Завтра в 18:00 по Москве состоится первый из интернет-туров COCI - хорватской олимпиады по программированию. Как обычно - шесть задач на три часа. Система - как на старых IOI (без фидбека, каждый тест оценивается в отдельности). Никакой мегасложной регистрации не надо - всего лишь регистрируемся в тестирующей системе и логинимся в COCI Contest #1.
От себя: мне нравятся такие туры. Очень вкусные задачки вкупе с кошерной системой оценки :-)
Спасибо yeputons за незаметно поданную идею запостить про COCI на КФ.
Для тех кто ещё не знает, вчера утром из жизни ушёл Стив Джобс.
Трудно оценить вклад этого человека в IT. Жаль, что такие великие люди уходят.
Ошибка выполнения [TIME_LIMIT_EXCEEDED]
=====
Использовано: 1 мс, 1332 КБ
Специально по просьбе JKeeJ1e30.
Задачи второго дивизиона и A с B первого уже разбирались ранее, поэтому я опишу только решения C и D.
C. Петя и Пауки
Поначалу могло показаться, что это задача на конструктив, но такую мысль нужно сразу откидывать. Конструктивные решения ломались тестами 4 4, 7 4 и 5 6.
Если заметить, что nm ≤ 40, и понять, что доску можно вращать, то из простого рассуждения, что меньшая сторона доски не больше 6, становится ясно, что задача - на какую-то динамику по профилю.
Моё решение - такое. Будем считать не максимальное количество оставшихся клеток, а минимальное количество центров, в которые могут сбежаться все пауки. Повернём доску, чтобы количество строк было не больше шести.
Пусть D[k][pmsk][msk] - это минимальное количество центров, достаточное, чтобы собрать всех тараканов с первых k столбцов, причём k-ый столбец имеет маску pmsk, а k+1-ый - msk. Тогда за переход мы перебираем маску tmsk k-1-ого столбца, и среди тех, для которых k-ый столбец может целиком разбежаться по центрам, выбираем тот, для которого D[k - 1][tmsk][pmsk] минимально.
Получается решение за O(n * 23m), где n > m.
Другие варианты решения, которые я видел:
Можно как-то схлопнуть две двоичных маски в одну троичную, честно говоря, я не вникал, как именно.
Можно насчитать ответ для всех входных данных, благо тех совсем немного, каким-нибудь оптимизированным перебором. Например, перебирая маски центров в порядке возрастания количества бит.
D. Петя и раскраски.
Тут нужно посидеть, подумать, и вывести пару формул.
Во-первых, когда m = 1, ответ - kn, потому как подходит любая раскраска.
Когда m > 1, обратим наши взоры на два крайних столбца. Проведём прямую справа от левого крайнего столбца. Слева и справа от неё должно быть одинаковое количество цветов - пусть X. Теперь заметим, что если начать двигать эту прямую направо, количестов различных цветов слева будет неуменьшаться, а справа - неувеличиваться. А раз эти два количества должны оставаться одинаковыми, то ни одного увеличения/уменьшения происходить не должно. Значит все возможные цвета, которые могут оказаться слева от прямой должны присутствовать в крайнем левом столбце, а все возможные цвета, который могут оказаться справа от прямой - в крайнем правом столбце.
Иными словами, множество цветов на всей доске должно иметь вид 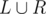 , где |L| = |R|, а множество цветов в левом и правом столбце - L и R соответственно. При этом заметим, что в оставшихся столбцах могут присутствовать только цвета из
, где |L| = |R|, а множество цветов в левом и правом столбце - L и R соответственно. При этом заметим, что в оставшихся столбцах могут присутствовать только цвета из  - иначе нам поломает всё условие.
- иначе нам поломает всё условие.
Что же, это даёт следующий алгоритм.
Зафиксируем 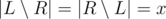 и
и 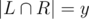 (должны выполняться условия 2x + y ≤ k и x + y ≤ n. Тогда во-первых, ответ нужно домножить на
(должны выполняться условия 2x + y ≤ k и x + y ≤ n. Тогда во-первых, ответ нужно домножить на 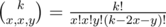 - это количество способов выбрать соответственно x, y и x цветов в множества
- это количество способов выбрать соответственно x, y и x цветов в множества  .
.
Далее, все клетки между крайними столбцами можно покрасить в произвольный из y цветов, значит ответ домножается на kn(m - 2).
Потом, нам надо покрасить крайние столбцы. Количество способов покрасить столбец в x цветов так, чтобы все цвета присутствовали, считается динамикой D[x] следующим образом: 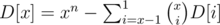 . Наконец, ответ домножается на вышепосчитанное D[x]2.
. Наконец, ответ домножается на вышепосчитанное D[x]2.
С реализацией этого решения может быть некоторое количество проблем. Я лично столкнулся с тем, что оно адски тормозило. Оказалось фатальным делать O(k) взятий обратного элемента за логарифм в лонг лонгах. Помогли следующие оптимизации - предподсчитываем все биномиальные коэффициенты до 2000, расписываем 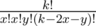 как
как 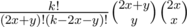 - последние два выражения у нас предподсчитаны. Можно было бы также просто предподсчитать обратные факториалы - у нас будет использоваться O(n) значений обратных факториалов.
- последние два выражения у нас предподсчитаны. Можно было бы также просто предподсчитать обратные факториалы - у нас будет использоваться O(n) значений обратных факториалов.
Конкретно реализацию можно посмотреть в моём, например, коде.
Присоединяюсь к общему вопросу: авторы, где разбор? А конкретно его часть, относящаяся к задаче E? :-)
Который год задумываюсь над таким вопросом. Вот мы заниемся алгоритмическим программированием в пределах одного потока - все олимпиадные задачи подразумевают решение без параллельного программирования.
А бывают ли контесты с задачами на параллельное программирование? Тема-то весьма интересная. Если кто знает, расскажите.
Сегодня утром листал хабр, натктнулся на интересный пост, жаль только, пока закрытый.
Там была ссылка на воспоминания советского программиста, начинавшего общение с компьютерами в середине шестидесятых годов. Что я могу сказать. Несмотря на то, что я опоздал родиться на полвека, я сегодня сидел и два часа зачитывался - так оно необычно.
Я так подумал, на Codeforces будет людям будет интересно почитать о другой стороне, о фундаменте и развитии всего того, чем мы сейчас занимаемся, причём с точки зрения советского человека.
Вот ссылки на две части этого чертовски интересного повествования.
[первая] [вторая]
Можно прокрутить пост до низу и прочитать доказательство корректности построения суммы Минковского, которе недавно обсуждалось на КФ.
Задача DIV1-A, DIV2-C Поезда.
К этой можно было подойти с двух сторон - как программист и как математик. Рассмотрим оба подхода.
Сначала запишем несколько общих суждений. Поставим на прямой все моменты времени, в которые приходят поезда. Будем относить отрезок между двумя соседними точками к той девушке, к которой идет поезд, соответствующий правому концу отрезка. Также заметим, что вся картина периодична с периодом lcm(a, b). Очевидно, что Вася будет чаще ездить к той девушке, суммарная длина отрезков которой больше.
Программистский подход заключается в моделировании процесса. Если нам надо сравнить длины двух множеств отрезков - давайте их посчитаем. Это делается с помощью двух указателей. Смотрим какой поезд поезд приедет следующим, прибавляем время до прихода этого поезда к одному из ответов, двигаем указатель и текущее время. Остановиться стоит либо когда два последних поезда пришли одновременно, либо когда пришло a+b поездов. Решение за O(a + b),что с запасом укладывается в ограничение по времени. Не забываем, при этом, что lcm(a,b) ~ 10^12, то есть нужен 64-битный тип данных.
Математический подход позволяет получить более изящное и короткое решение, однако придется больше подумать. Кажется очевидным, что чаще Вася будет ездить к той девушке, к которой чаще ходят поезда. Этот факт почти верен. Попробуем его доказать. Сократим периоды a и b на их gcd - от этого, очевидно, ничего не изменится. Пусть для определенности a ≤ b. Посчитаем суммарную длину отрезков, соответствующих второй девушке. Для этого заметим несколько фактов.
1) Все они не превосходят a
2) Все a отрезков различны (из-за взаимной простоты).
3) Все они хотя бы 1.
Но такое множество отрезков - единственное и его длина равна 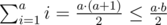 . Причем равенство достигается при b - a = 1. Значит верно следующее. Ответ равен Equal, когда |a - b| = 1, иначе чаще Вася ездит к девушке к которой чаще ходят поезда. Главное не забыть поделить a и b на их gcd.
. Причем равенство достигается при b - a = 1. Значит верно следующее. Ответ равен Equal, когда |a - b| = 1, иначе чаще Вася ездит к девушке к которой чаще ходят поезда. Главное не забыть поделить a и b на их gcd.
Задача Div1-B, Div2-D Вася и Типы.
В этой задаче нужно было написать ровно то, что написано в условии задачи, практически за любую сложность.
Предлагается делать это так. Для каждого типа данных будем хранить два значения – его имя и количество звездочек при его приведении к void. Тогда запрос typeof обрабатывается пробегом по массиву определений, в котором мы находим нужное нам имя типа, и количество звездочек в нем.
Тип errtype удобно хранить как void, к которому приписали - inf звездочек.
Таким образом, выполняя запрос typedef, мы находим количество звёздочек при типе A, добавляем к нему количество звездочек и вычитаем количество амперсандов. Не забываем заменять любое отрицательное число звездочек на - inf, и создавать новое определение типа B, удаляя старое.
Задача Div1-C, Div2-E Интересная игра.
В этой задаче нужно провести анализ игры. Однако, из-за того что каждым ходом игра распадается на несколько независимых, анализ можно провести с помощью функции Гранди (можно почитать здесь, здесь или здесь). Остается построить переходы для каждой позиции. Можно строить переходы отдельно для каждой вершины, решая O(sqrt(n)) несложных линейных уравнений. Можно построить все разбиения заранее, просто перебирая наименьший член и количество, и вылетая, когда сумма превосходит n. Второй способ лучше, потому что он работает за O(m + n), где m - количество рёбер, а первый - за O(nsqrt(n)), что побольше.
Оценим m в максимальном тесте. Рёбер - не более 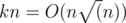 . Однако на практике их гораздо меньше - порядка 520 тысяч. Соответственно, рёбра вполне можно успеть построить за время O(nk).
. Однако на практике их гораздо меньше - порядка 520 тысяч. Соответственно, рёбра вполне можно успеть построить за время O(nk).
Можно попытаться посчитать функцию Гранди по определению - ксоря все нужные значения для каждой позиции. Но такое решение не проходит - слишком много длинных разбиений.
Научимся для длинного разбиения быстро считать ксор функций Гранди. Используем стандартный прием для подсчета функций на отрезке - xor[l, r] = xor[0, r] xor[0, l - 1]. По ходу алгоритма будем поддерживать в xor[i] ксор на префиксе до i. Тогда и ксор на отрезке можно посчитать за O(1). Решение получилось строго за количество рёбер, которое не очень велико.
Задача Div1-D. Красивая дорога.
В этой задаче надо для каждого ребра посчитать количество путей, на которых оно является максимальным. Так как для одного ребра отдельно не кажется возможным посчитать ответ быстрее, чем за линейное время, решение будет обрабатывать все ребра вместе.
Решим задачу сначала для двух крайних случаев, потом, объединив эти два, получим полное решение.
Первый случай - когда веса всех ребер одинаковы. В таком случае можно решить задачу обходом в глубину. Для каждого ребра нам просто нужно посчитать количество путей, которые проходят по этому ребру. Это количество есть произведение количеств вершин по разные стороны ребра. Если мы посчитаем количество вершин с одной стороны от него, тогда зная общее количество вершин в дереве, легко найти количество вершин по другую сторону от него, а значит и требуемое количество путей, на которых оно лежит.
Второй случай – когда веса всех ребер различны. Отсортируем ребра в порядке возрастания веса. Изначально возьмём граф, в котором нет рёбер. Будем добавлять по ребру в порядке возрастания веса, для каждого ребра объединяя компоненты связности, которые оно соединяет. Тогда ответ для каждого нового добавленного ребра – произведение размеров компонент, которые оно соединило.
Теперь надо объединить эти два случая. Будем добавлять ребра по возрастанию, но не по одному, а группами одинокого веса. Поймём, что является ответом для каждого из добавленных рёбер. После добавления наших рёбер образовалось некоторое количество компонент связности - для каждого ребра мы считаем то самое произведение количеств вершин по разные его стороны внутри его новообразовавшейся компоненты связности.
Для того, чтобы посчитать это самое количество рёбер по разные его стороны, поймём, что от старых компонент связности достаточно знать лишь их размеры, и связи между ними - то, как они были устроены нам не важно. Воспользуемся системой непересекающихся множеств: добавляя рёбра в наш лес мы объединяем старые компоненты связности по этим рёбрам. Заметим, что до объединения компонент мы должны посчитать ответ для наших рёбер - а это можно сделать обходом в глубину на нашем сжатом дереве как в первом случае, только вместо количества вершин по разные стороны от ребра мы берём сумму размеров компонент связности по разные стороны от ребра.
Как это аккуратно реализовать:
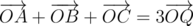 . Вполне логично, что надо понять какое множество точек задает это
. Вполне логично, что надо понять какое множество точек задает это 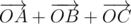 , научится его строить и проверять точку на принадлежность ему. Такое множество называется суммой Минковского. Из его свойств нам понадобится только одно: сумма двух выпуклых многоугольников - выпуклый многоугольник, причем стороны многоугольника совпадают, как вектора, со сторонами исходных многоугольников. Докажем это позже.
, научится его строить и проверять точку на принадлежность ему. Такое множество называется суммой Минковского. Из его свойств нам понадобится только одно: сумма двух выпуклых многоугольников - выпуклый многоугольник, причем стороны многоугольника совпадают, как вектора, со сторонами исходных многоугольников. Докажем это позже. 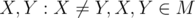 . По определению
. По определению 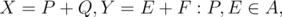 Q,
Q, 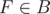 (здесь и далее точка отождествляется со своим радиус-вектором).
(здесь и далее точка отождествляется со своим радиус-вектором). 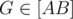 . Докажем, что
. Докажем, что 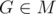 .
. 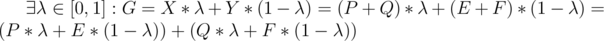 .
.  - в противном случае
- в противном случае 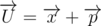 . Понятно, что x и p - самые нижние точки многоугольников A и B - в противном случае одну из них можно сдвинуть на малый вектор d, лежащий в нижней полуплоскости, так, что точка останется внутри своего многоугольника. При этом U сдвинется так же на d, что противоречит тому, что U - одна из нижних точек многоугольника.
. Понятно, что x и p - самые нижние точки многоугольников A и B - в противном случае одну из них можно сдвинуть на малый вектор d, лежащий в нижней полуплоскости, так, что точка останется внутри своего многоугольника. При этом U сдвинется так же на d, что противоречит тому, что U - одна из нижних точек многоугольника. 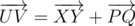 .
.| Название |
|---|


