Введение
Пусть нам дана следующая задача:
Вам необходимо найти $$$n$$$ — ное число Фибоначчи ($$$n$$$ — натуральное число, $$$n \leq 10^6$$$). Последовательность Фибоначчи задается следующим образом:
- $$$F_1 = 1$$$
- $$$F_2 = 1$$$
- $$$F_i = F_{i - 1} + F_{i - 2}$$$ $$$^{*1}$$$
Поскольку $$$n$$$ — ное число может быть очень большим, то выведите его по модулю $$$10^9 + 7$$$.
Сразу после прочтения данной задачи, всем в голову приходит очевидное решение задачи.
Очевидное решение задачи
Мы будем хранить массив $$$fib$$$, в котором будут наши числа Фибоначчи, а их индексы будут обозначать какими по порядку идут эти числа. Мы запишем для удобства первые два числа из последовательности в наш массив ($$$fib[1] = 1, fib[2] = 1$$$).
Далее, мы, начиная с 3 — его элемента, будем вычислять $$$i$$$ — ое число Фибоначчи как сумму двух предыдущих (см. пункт $$$^{*1}$$$ ). То есть $$$fib[i] = fib[i - 1] + fib[i - 2]$$$ (надо не забывать, что еще нужно смотреть вычисление по модулю, поэтому $$$fib[i] = (fib[i - 1] + fib[i - 2])$$$ $$$\%$$$ $$$mod$$$, где $$$mod = 10^9 + 7$$$ по условию). Будем мы делать такие вычисления до тех пор, пока не дойдем до $$$n$$$ — ного числа. И далее мы просто выведем $$$fib[n]$$$.
Нетрудно оценить время работы — оно будет $$$O(n)$$$, поскольку для каждого числа до $$$n$$$ мы вычисляем за $$$O(1)$$$ его значение. И казалось бы, мы решили задачу, но представим другую ситуацию. Пусть $$$n$$$ имеет значение до $$$10^9$$$, и ограничение по времени на задачу $$$1$$$ секунда, а по памяти такое, что не позволит хранить массив. Мы можем решать такую задачу и без массива, но и это сильно не повлияет на асимптотику кода по времени в $$$O(n)$$$, которое не сможет выполниться за $$$1$$$ секунду. Нам нужно более оптимальное решение, о котором я расскажу далее. Но чтобы его осознать, нам нужно познакомиться с поверхностной теорией о матрицах.
Немного о матрицах
Я буду использовать следующую небольшую терминологию.
Давайте научимся делать следующие три алгебраические операции: сложение, вычитание и умножение. Начнем со сложения и вычитания.
Сложение и вычитание матриц
Складывать и вычитать 2 матрицы мы можем только в том случае, когда они имеют одинаковый размер, то есть одинаковое количество строк и столбцов. Например, следующие две матрицы мы можем сложить:
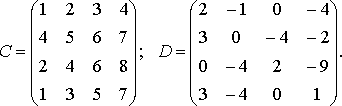
А если бы у какой-то из этих матриц отличалось количество строк или столбцов, то мы не смогли бы сложить.
Суммой матриц $$$A$$$ и $$$B$$$ с размерами $$$n$$$ x $$$m$$$ называется матрица $$$C$$$ с размером $$$n$$$ x $$$m$$$, все элементы которой равны попарной сумме всех соответствующих элементов матриц $$$A$$$ и $$$B$$$, то есть каждый элемент матрицы $$$C$$$ равен: $$$c_{ij} = a_{ij} + b_{ij}$$$, где $$$i$$$ обозначает строку, а $$$j$$$ — столбец ($$$1 \leq i \leq n, 1 \le j \leq m$$$).
Так как любое вычитание можно заменить сложением (напр. $$$7 - 5 = 7 + (-5)$$$), то вычитание матриц $$$A$$$ и $$$B$$$ можно также заменить суммой матрицы $$$A$$$ и противоположной матрицы $$$B$$$, то есть $$$A - B = A + (-B)$$$.
Пример суммы матриц:
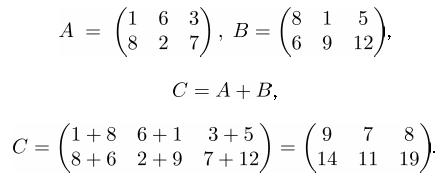
Пример разности матриц:

Также существуют некоторые свойства сложения матриц.
Умножение матриц
Умножать матрицу $$$A$$$ на $$$B$$$ можно только в том случае, если количество столбцов матрицы $$$A$$$ совпадает с количеством строк матрицы $$$B$$$. Например, следующие две матрицы можно умножить:
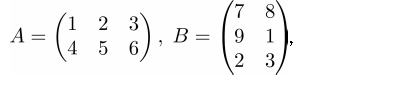
Умножение матриц (обозначается как $$$AB$$$, реже — $$$A$$$ x $$$B$$$) — это операция вычисления матрицы $$$C$$$, каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго, или по-другому:
$$$c_{ij} = \sum\limits_{k = 1}^n a_{ik} + b_{kj}$$$
Если матрица $$$A$$$ имеет размеры $$$n$$$ x $$$m$$$, а матрица $$$B$$$ — $$$m$$$ x $$$k$$$, то матрица $$$C$$$ будет иметь размер $$$n$$$ x $$$k$$$.
И для умножения матриц существует свои свойства.
Пример умножения матриц (на основе предыдущей картинки):

Теперь, когда мы познакомились с небольшой теорией о матрицах, мы можем приступить к оптимальному решению нашей задачи.
Оптимальное решение задачи
Давайте будем представлять два подряд идущих элемента последовательности Фибоначчи как вектор-строку с размерам $$$1$$$ x $$$2$$$, то есть:

Нам нужно научиться умножать нашу вектор-строку на какую-то матрицу $$$A$$$, чтобы мы смогли получить следующую вектор-строку, то есть:
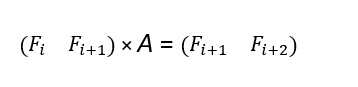
Так как количество строк первой матрицы такое же, как и у итоговой матрицы, то это означает, что мы можем подобрать некоторую матрицу $$$A$$$.
Поскольку мы знаем размеры первого множителя и того, что получилось в результате умножения, то мы сможем узнать размеры матрицы $$$A$$$ — это будет $$$2$$$ x $$$2$$$ (Поскольку количество строк у матрицы $$$A$$$ должно совпадать с количеством столбцов первой матрицы, а количество столбцов итоговой матрицы должно совпадать с количеством столбцов матрицы $$$A$$$). То есть матрица $$$A$$$ имеет вид:
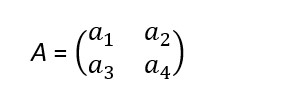
Давайте найдем произведение первой вектор-строки и матрицы $$$A$$$:

Нам надо, чтобы выполнилось следующее равенство:

А так как мы знаем, что $$$F_{i + 2} = F_{i + 1} + F_{i}$$$, то $$$a_2 = 1$$$, $$$a_4 = 1$$$. И поскольку очевидно, что $$$F_{i + 1} = F_{i + 1}$$$, то $$$a_1 = 0$$$, $$$a_3 = 1$$$. Получается, что матрица $$$A$$$ будет иметь вид:

Мы нашли такую матрицу $$$A$$$, что умножив на нее матрицу из двух чисел Фибоначчи с индексами $$$i$$$, $$$i + 1$$$, мы получаем новую матрицу из двух чисел Фибоначчи с индексами $$$i + 1$$$, $$$i + 2$$$. Поэтому следующее выражение будет верно:
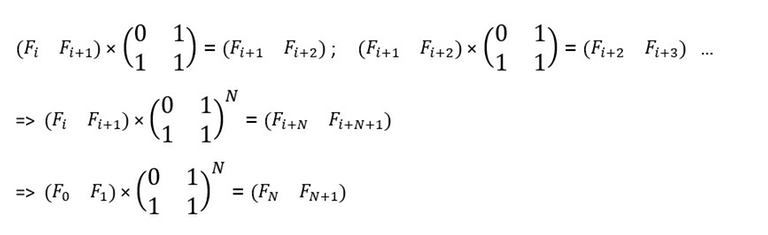
Наше решение будет заключаться в том, что мы вектор-строку с числами Фибоначчи с индексами $$$0$$$ и $$$1$$$ ($$$F_0 = 0$$$, $$$F_1 = 1$$$) будем умножать на матрицу $$$A$$$ в степени $$$n$$$, а затем из итоговой вектор-строки выведем первое число (то есть число, стоящее на пересечении $$$1$$$ — ой строки и $$$1$$$ — ого столбца).
И как многие уже догадались, мы будем возводить матрицу $$$A$$$ в степень $$$n$$$ при помощи быстрого возведения в степень. Для матрицы $$$A$$$ она будет выглядеть так:
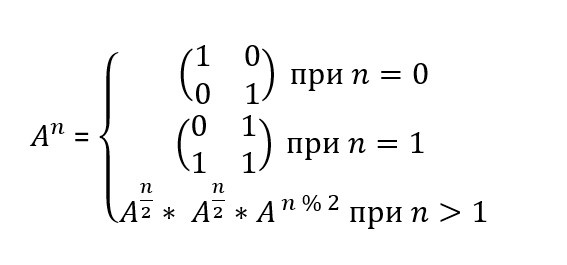
В данном случае, $$$\frac{n}{2}$$$ обозначает деление $$$n$$$ на $$$2$$$ с округлением вниз, а $$$n$$$ % $$$2$$$ — остаток при делении на $$$2$$$. Больше информации про быстрое возведение в степень можно найти в интернете.
Все! Мы научились решать данную задачу, осталось ее реализовать.
Асимптотика по времени данного кода будет составлять $$$O(log_2 n)$$$, поскольку мы вычисляем $$$F_n$$$ — ное число Фибоначчи при помощи быстрого возведения в степень, асимптотика которого как раз составляет $$$O(log_2 n)$$$. И поэтому время выполнения кода будет гораздо быстрее, чем $$$1$$$ секунда.









