The official implementations of all the problems are here.
(problems D', H', etc. were not used)
- Feb 19, 2022: I proposed problem D' to Codeforces Round 778 (Div. 1 + Div. 2, based on Technocup 2022 Final Round), but it was not used.
- Mar 13, 2023: I invented problem A.
- May 16: I invented problem H'.
- May 19: I realized problem G can be solved in $$$O(n)$$$ time and we used it in the Italian team selection test for IOI.
- Jul 04: I opened a Div. 1 proposal containing A, D', G, H' and other problems which are not going to be used.
- Aug 09: I invented problem I, with intended solution in $$$O(n^3)$$$.
- Sep 27: I invented problem C.
- Oct 14: errorgorn replied to my contest proposal.
- Nov 02: I invented problem D''. errorgorn solved problem I in $$$O(n^2 \log n)$$$.
- Nov 08: I invented problems E and F. I didn't propose problem F because I thought it was too easy.
- Nov 10: I invented problem H with $$$O(n \log n)$$$ operations. We had a preliminary problemset, with problems A, D', C, D'', E, H1, G, H', I. I started preparing the problems.
- Nov 14: I finished preparing the problems, and the round was ready for testing. dario2994 tested and didn't solve problem D''. I realized the official solution of problem D'' was wrong (and now I don't have any solution).
- Nov 15: I removed problem D'' from the contest and replaced it with problem F.
- Nov 17: I invented problem E'.
- Nov 19: I invented problem F', which was rejected because it was proposed independently to errorgorn by the authors of another round.
- Nov 22: gamegame tested and said problem H' is well-known in China. I removed it.
- Nov 26: we realized problem D' was too hard for position B.
- Nov 28: I invented problem D with $$$k = 1$$$ and $$$a_i \geq 2$$$, and I proposed it as B.
- Nov 29: I invented problem B. Endagorion solved problem H in $$$2n$$$ operations.
- Dec 07: the problemset was A, B, C, D', F1, F2, E, G, H1, H2, I, but there was a huge gap between D' and the next problems. We ended up using A, B, C, D, E', E, F2, G, H2, I (i.e., 10 problems). D still had $$$k = 1$$$ and $$$a_i \geq 2$$$.
- Dec 13: we removed the constraints $$$k = 1$$$ and $$$a_i \geq 2$$$ from problem D.
- Dec 18: problem E' appeared in Educational Codeforces Round 160 (Rated for Div. 2). We removed it and we decided to use subtasks on problem F.
Author: TheScrasse
Preparation: TheScrasse
Suppose you can only use $$$\texttt{U}$$$, $$$\texttt{R}$$$, $$$\texttt{D}$$$. Which cells can you reach?
If you only use buttons $$$\texttt{U}$$$, $$$\texttt{R}$$$, $$$\texttt{D}$$$, you can never reach the points with $$$x < 0$$$. However, if all the special points have $$$x \geq 0$$$, you can reach all of them with the following steps:
- visit all the special points with $$$x = 0$$$, using the buttons $$$\texttt{U}$$$, $$$\texttt{D}$$$;
- press the button $$$\texttt{R}$$$ to reach $$$x = 1$$$;
- visit all the special points with $$$x = 1$$$, using the buttons $$$\texttt{U}$$$, $$$\texttt{D}$$$;
- $$$\dots$$$
- visit all the special points with $$$x = 100$$$, using the buttons $$$\texttt{U}$$$, $$$\texttt{D}$$$.
Similarly, if you use at most $$$3$$$ buttons in total, you can reach all the special points if at least one of the following conditions is true:
- all $$$x_i \geq 0$$$;
- all $$$x_i \leq 0$$$;
- all $$$y_i \geq 0$$$;
- all $$$y_i \leq 0$$$.
Complexity: $$$O(n)$$$
1909B - Make Almost Equal With Mod
Author: TheScrasse
Preparation: TheScrasse
Find a value of $$$k$$$ that works in many cases.
$$$k = 2$$$ works in many cases. What if it does not work?
If $$$k = 2$$$ does not work, either all the numbers are even or all the numbers are odd. Which $$$k$$$ can you try now?
Let $$$f(k)$$$ be the number of distinct values after the operation, using $$$k$$$.
Let's try $$$k = 2$$$. It works in all cases, except when either all the numbers are even or all the numbers are odd.
Let's generalize. If $$$a_i \text{ mod } k = x$$$, one of the following holds:
- $$$a_i \text{ mod } 2k = x$$$;
- $$$a_i \text{ mod } 2k = x+k$$$;
It means that, if $$$f(k) = 1$$$ (i.e., all the values after the operations are $$$x$$$), either $$$f(2k) = 1$$$ (if either all the values become $$$x$$$, or they all become $$$x+k$$$), or $$$f(2k) = 2$$$.
Therefore, it is sufficient to try $$$k = 2^1, \dots, 2^{57}$$$. In fact, $$$f(1) = 1$$$ and $$$f(2^{57}) = n$$$, so there must exist $$$m < 57$$$ such that $$$f(2^m) = 1$$$ and $$$f(2^{m+1}) \neq 1 \implies f(2^{m+1}) = 2$$$.
Alternative (more intuitive?) interpretation:
- $$$a_i \text{ mod } 2^j$$$ corresponds to the last $$$j$$$ digits in the binary representation of $$$a_i$$$. There must exist $$$j$$$ such that the last $$$j$$$ digits make exactly $$$2$$$ distinct blocks.
In the following picture, $$$a = [1005, 2005, 7005, 11005, 16005]$$$ and $$$k = 16$$$:

Complexity: $$$O(n \log(\max a_i))$$$
Author: TheScrasse
Preparation: TheScrasse
Assign bigger costs to shorter intervals.
Solve the problem with $$$n = 2$$$.
Solve the following case: $$$l = [1, 2]$$$, $$$r = [3, 4]$$$, $$$c = [1, 2]$$$. Can you generalize it?
You have to match each $$$l_i$$$ with some $$$r_j > l_i$$$.
Construct $$$v = {l_1, l_2, \dots, l_n, r_1, r_2, \dots, r_n}$$$ and sort it. If you replace every $$$l_i$$$ with the symbol $$$\texttt{(}$$$ and every $$$r_i$$$ with the symbol $$$\texttt{)}$$$, you get a regular bracket sequence (sketch of proof: $$$l_i < r_i$$$ for each $$$i$$$, so each prefix of symbols contains at least as many $$$\texttt{(}$$$ as $$$\texttt{)}$$$, so the bracket sequence is regular).
Now match each $$$\texttt{(}$$$ with the corresponding $$$\texttt{)}$$$. You can show that this is the optimal way to rearrange the $$$l_i$$$ and the $$$r_i$$$. (From now, let the $$$l_i$$$, $$$r_i$$$ and $$$c_i$$$ be the values after your rearrangement.)
Proof:
- If you match the brackets in any other way, you get two intervals such that their intersection is non-empty but it is different from both intervals (i.e., you get $$$l_i < l_j < r_i < r_j$$$).
- You have also assigned some cost $$$c_i$$$ to $$$[l_i, r_i]$$$ and $$$c_j$$$ to $$$[l_j, r_j]$$$. Without loss of generality, $$$c_i \leq c_j$$$ (the other case is symmetrical).
- If you swap $$$r_i$$$ and $$$r_j$$$, the cost does not increase.
- Keep swapping endpoints until you get the "regular" bracket matching. You can show that the process ends in a finite number of steps. For example, you can show that $$$\sum ((r_i - l_i)^2)$$$ strictly increases after each step, and it is an integer $$$\leq \sum (r_i^2)$$$.
Now, you can get the minimum cost by sorting the intervals by increasing length and sorting the $$$c_i$$$ in decreasing order.
Alternative (more intuitive?) interpretation:
- If you solve the problem with $$$n = 2$$$ and try to generalize, you can notice that it seems optimal to match every $$$r_i$$$ with the largest unused $$$l_i$$$ (if you iterate over $$$r_i$$$ in increasing order).
You can implement the solution by using either a stack (to simulate the bracket matching) or a set (to find the largest unused $$$l_i$$$).
Complexity: $$$O(n \log n)$$$
Author: TheScrasse
Preparation: TheScrasse
Solve the problem with $$$k = 0$$$.
Solve the problem with generic $$$k$$$. When is the answer $$$-1$$$?
Do you notice any similarities between the cases with $$$k = 0$$$ and with generic $$$k$$$?
Consider the "shifted" problem, where each $$$x$$$ on the blackboard (at any moment) is replaced with $$$x' = x-k$$$.
Now, the operation becomes "replace $$$x$$$ with $$$y+z$$$ such that $$$y+z = x+k \implies (y'+k)+(z'+k) = (x'+k)+k \implies y'+z' = x'$$$". Therefore, in the shifted problem, $$$k' = 0$$$.
Now you can replace every $$$a'_i := a_i - k$$$ with any number of values with sum $$$a'_i$$$, and the answer is the amount of numbers on the blackboard at the end, minus $$$n$$$.
If we want to make all the values equal to $$$m'$$$, it must be a divisor of every $$$a'_i$$$.
- If all the $$$a'_i$$$ are positive, it is optimal to choose $$$m' = \gcd a'_i$$$.
- If all the $$$a'_i$$$ are zero, the answer is $$$0$$$.
- If all the $$$a'_i$$$ are negative, it is optimal to choose $$$m' = -\gcd -a'_i$$$.
- Otherwise, the answer is $$$-1$$$.
Alternative way to get this result:
- You have to split each $$$a_i$$$ into $$$p_i$$$ pieces equal to $$$m$$$, and their sum must be equal to $$$a_i + k(p_i - 1) = (a_i - k) + kp_i = mp_i$$$. Then, $$$(a_i - k) = (m - k)p_i$$$, so $$$m' = m-k$$$ must be a divisor of every $$$a'_i = a_i - k$$$.
In both the positive and the negative case, you will only write positive elements (in the original setup), as wanted.
- If all the $$$a'_i$$$ are positive, the numbers you will write on the shifted blackboard are positive, so they will be positive also in the original blackboard.
- If all the $$$a'_i$$$ are negative, the numbers you will write on the shifted blackboard are greater than the numbers you will erase, so they will be greater than the numbers in input (and positive) in the original blackboard.
Complexity: $$$O(n + \log(\max a_i))$$$
Author: TheScrasse
Preparation: TheScrasse
Find a strategy that turns "few" lamps on in most cases.
Pressing all the buttons turns $$$\lfloor \sqrt n \rfloor$$$ lamps on.
If the strategy in Hint 2 does not work, at most $$$3$$$ lamps must be on at the end.
Iterate over all subsets of at most $$$3$$$ lamps that must be on at the end.
If you press all the buttons, lamp $$$i$$$ is toggled by all the divisors of $$$i$$$, so it will be on if $$$i$$$ has an odd number of divisors, i.e., if $$$i$$$ is a perfect square.
Then, the strategy of pressing all the buttons works if $$$\lfloor \sqrt n \rfloor \leq \lfloor n/5 \rfloor$$$, which is true for $$$n \geq 20$$$.
If $$$n \leq 19$$$, at most $$$\lfloor 19/5 \rfloor = 3$$$ lamps must be turned on at the end.
If you know which lamps must be turned on at the end, you can iterate over the buttons from $$$1$$$ to $$$n$$$ and press button $$$i$$$ if and only if lamp $$$i$$$ is in the wrong state. So you can iterate over all subsets of at most $$$3$$$ lamps, and check if the corresponding choice of buttons is valid (i.e., the $$$m$$$ constraints hold). You can remove a $$$\log n$$$ factor by precalculating the choice of buttons for all small subsets before running the testcases.
Complexity for each test: $$$O(\sum n + (\sum m \cdot k^{2k-4}))$$$ (if $$$\lfloor n/k \rfloor$$$ lamps must be on; in this case, $$$k = 5$$$).
1909F1 - Small Permutation Problem (Easy Version), 1909F2 - Small Permutation Problem (Hard Version)
Author: TheScrasse
Preparation: TheScrasse
Find a clean way to visualize the problem.
Draw a $$$n \times n$$$ grid, with tokens in $$$(i, p_i)$$$. Which constraints on the tokens do you have?
You have some "L" shapes, and each of them must contain a fixed number of tokens (in 1909F1 - Small Permutation Problem (Easy Version) the shapes are $$$1$$$ cell wide and must contain at most $$$2$$$ tokens). Iterate over the shapes in increasing order of $$$i$$$.
Split each shape into $$$2$$$ rectangles and iterate over the number of tokens in the first rectangle.
Draw a $$$n \times n$$$ grid, with tokens in $$$(i, p_i)$$$.
Consider any $$$a_i \neq -1$$$ and the nearest $$$a_j \neq -1$$$ on the left (if it does not exist, let's set $$$j = a_j = 0$$$). Then, there must be $$$a_i$$$ tokens in the subgrid $$$[1, i] \times [1, i]$$$. We can suppose we have already inserted the $$$a_j$$$ tokens in $$$[1, j] \times [1, j]$$$, and we have to insert $$$a_i - a_j$$$ tokens in the remaining cells of $$$[1, i] \times [1, i]$$$ (they make an "L" shape).
WLOG, the $$$a_j$$$ tokens in $$$[1, j] \times [1, j]$$$ are in the cells $$$(1, 1), \dots, (a_j, a_j)$$$. Then, we can put tokens in the blue cells in the picture.
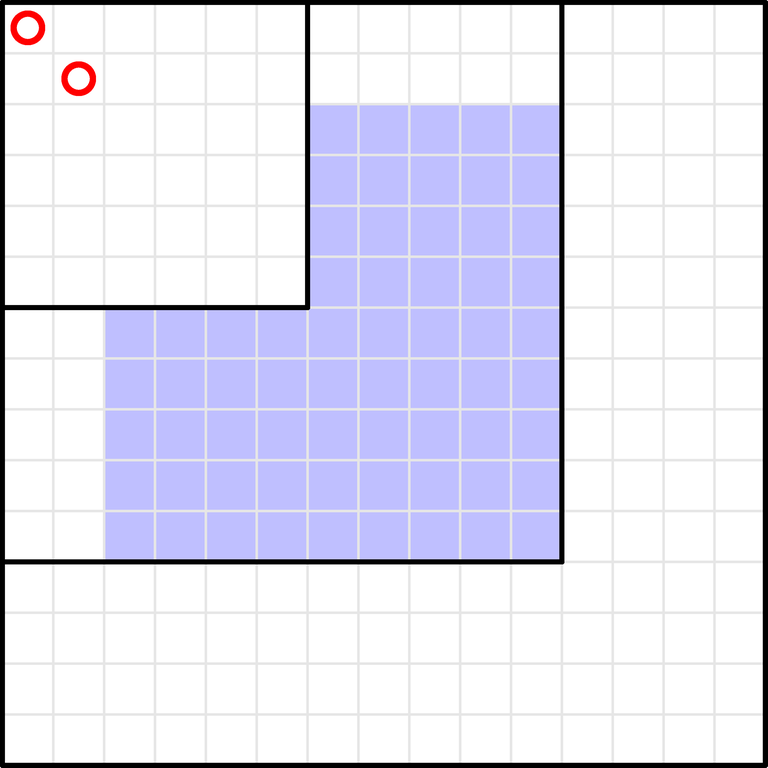
The blue shape can be further split into these two rectangles:
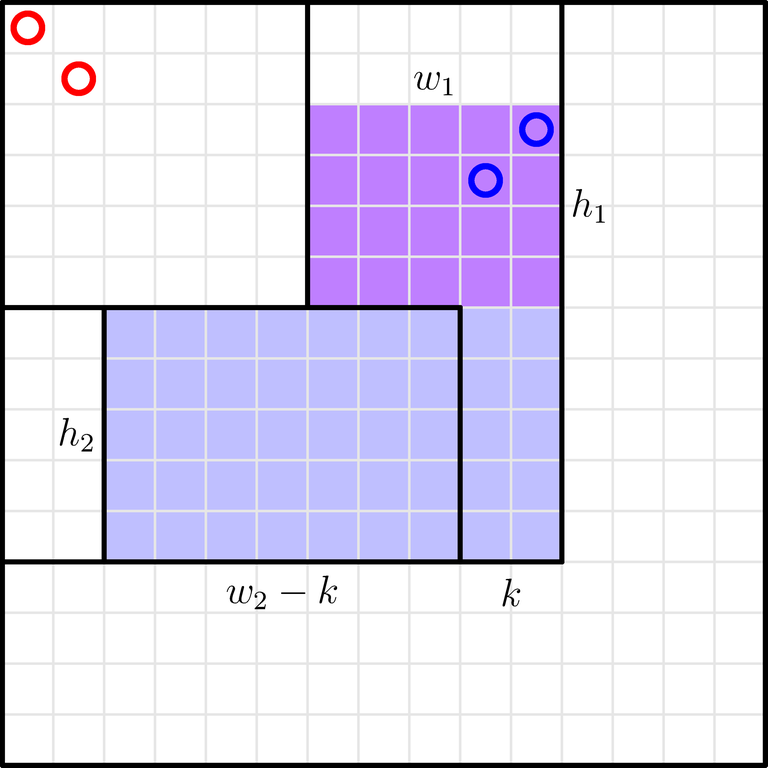
Iterate over $$$k$$$, the number of tokens in the first rectangle ($$$0 \leq k \leq a_i - a_j$$$). Then, you have to insert $$$k$$$ tokens into a $$$h_1 \times w_1$$$ rectangle, and the remaining $$$a_i - a_j - k$$$ tokens into a $$$h_2 \times (w_2 - k)$$$ rectangle.
The number of ways to insert $$$k$$$ tokens into a $$$h \times w$$$ rectangle is equal to the product of the number of ways to choose $$$k$$$ rows, the number of ways to choose $$$k$$$ columns, and the number of ways to fill the resulting $$$k \times k$$$ subgrid: the result is $$$\binom{h}{k} \binom{w}{k} k!$$$.
$$$a_n = n$$$ automatically (if $$$a_n \neq n$$$ and $$$a_n \neq -1$$$, the answer is $$$0$$$). If the non-negative $$$a_i$$$ are non-decreasing, the sum of the $$$a_i - a_j + 1$$$ (i.e., the $$$k$$$ over which you have to iterate) is $$$O(n)$$$, so the algorithm is efficient enough. Otherwise, the answer is $$$0$$$.
Complexity: $$$O(n)$$$
Author: TheScrasse
Preparation: TheScrasse
If you remove the condition $$$s = x+y+z$$$, the problem becomes harder.
Solve for a fixed $$$|y|$$$ (length of $$$y$$$).
Suppose you have found a valid $$$y$$$. Shift it one position to the right. When is it still valid?
The valid $$$y$$$ with $$$|y| = l$$$ start in consecutive positions.
Using the same idea of the proof of Hint 4, you can find all the valid $$$y$$$.
Let's use
Unable to parse markup [type=CF_MATHJAX]
to indicate the substring $$$[l, r]$$$ of $$$s$$$. Let's use $$$(a, b)$$$ to indicate the triple of strings $$$(s[1, a], s[a+1, b], s[b+1, n])$$$.Suppose $$$(a, b)$$$ is valid. Then, $$$(a+1, b+1)$$$ is valid if and only if $$$s_{b+1} = t_{b+1}$$$.
If $$$(a, b)$$$ is valid, $$$s[1, b] = t[1, b]$$$; so if $$$s_b \neq t_b$$$, $$$(a+k, b+k)$$$ is invalid for $$$k \geq 0$$$. Therefore, if $$$(a, b)$$$ is the first valid pair with $$$b-a=l$$$ (i.e., with $$$|y| = l$$$), and $$$k$$$ is the smallest positive integer such that $$$(a+k, b+k)$$$ is invalid, then $$$s_{b+k} \neq t_{b+k}$$$, so the only valid pairs with $$$|y| = l$$$ are the $$$(a+j, b+j)$$$ with $$$0 \leq j < k$$$ (i.e., the valid $$$y$$$ with $$$|y| = l$$$ start in consecutive positions).
Now let's find all the valid $$$y$$$ with $$$|y| = l$$$. Suppose $$$(a, b)$$$ is valid, and $$$c$$$ is the minimum index such that $$$s_c \neq t_c$$$. Then, $$$b < c$$$, and $$$(a+k, b+k)$$$ is valid for all $$$b \leq b+k < c$$$. Similarly, if $$$d$$$ is the minimum integer such that $$$s_{n-d} \neq t_{m-d}$$$, $$$(a+k, b+k)$$$ is valid for all $$$n-d < a+k \leq a \implies n-d+l < b+k \leq b$$$.
Therefore, it's enough to check only one pair for each length, with $$$b$$$ in $$$[n-d+l+1, c-1]$$$ (because either all these pairs are valid or they are all invalid). This is possible by precomputing the rolling hash of the two strings. Alternatively, you can use z-function.
Complexity: $$$O(n)$$$
Author: TheScrasse
Full solution: Endagorion, errorgorn
Preparation: TheScrasse, francesco
Find a strategy which is as simple and "easy to handle" as possible.
Only perform operations such that all swapped pairs have $$$a_i > a_{i+1}$$$. Let's call such subarrays "swappable".
First, for each $$$i$$$ from left to right, do the operation on $$$[j, i]$$$, where $$$j$$$ is the minimum index such that $$$[j, i]$$$ is swappable.
Repeat the same algorithm from right to left.
After Hints 3 and 4, the array is sorted. Prove it (it will be useful).
Assign $$$\texttt{B}$$$ to the indices $$$i$$$ such that $$$a_i < a_{i-1}$$$ and $$$\texttt{A}$$$ to the other indices. During the process in Hint 3, after the operation on index $$$i$$$, which properties do $$$\texttt{A}$$$, $$$\texttt{B}$$$ have in the prefix $$$[1, i]$$$?
Answer to Hint 6:
- the values of type $$$\texttt{A}$$$ are increasing;
- there are no two consecutive elements of type $$$\texttt{B}$$$.
The rest of the proof (i.e., what happens during the process in Hint 4) is relatively easy.
Now let's find an efficient implementation. We have to use the properties in Hint 7.
You have to find the longest $$$\texttt{AB} \dots \texttt{AB}$$$ ending in position $$$i$$$, and perform the operation on it. What happens during the operation?
$$$\texttt{A}$$$ will always remain $$$\texttt{A}$$$. For each $$$\texttt{B}$$$, you have to detect when it becomes $$$\texttt{A}$$$.
For each $$$\texttt{B}$$$, you can precompute the number of moves needed to make it $$$\texttt{A}$$$.
For example, you can use a segment tree with the following information: the type of each element, the positions of the elements of type $$$\texttt{B}$$$, and the number of moves required for each $$$\texttt{B}$$$ to become $$$\texttt{A}$$$.
Let's only perform operations such that all swapped pairs have $$$a_i > a_{i+1}$$$. Let's call such subarrays "swappable".
- First, for each $$$i$$$ from left to right, do the operation on $$$[j, i]$$$, where $$$j$$$ is the minimum index such that $$$[j, i]$$$ is swappable (let's call it "operation $$$1.i$$$").
- Then, for each $$$i$$$ from right to left, do the operation on $$$[j, i]$$$, where $$$j$$$ is the minimum index such that $$$[j, i]$$$ is swappable (let's call it "operation $$$2.i$$$").
After these operations, the array is sorted. Let's prove it.
Assign $$$\texttt{B}$$$ to the indices $$$i$$$ such that $$$a_i < a_{i-1}$$$ and $$$\texttt{A}$$$ to the other indices. After operation $$$1.i$$$, only assign letters in the prefix $$$[1, i]$$$ and ignore the other elements. During the operations $$$2.i$$$, assign letters to all the elements.
Most of the following proofs are by induction. After the operation $$$1.i$$$ (supposing the properties were true after the operation $$$1.(i-1)$$$):
- An element of type $$$\texttt{A}$$$ will always remain of type $$$\texttt{A}$$$. Proof: the only elements of type $$$\texttt{A}$$$ whose previous element changes are the ones in the subarray $$$[j, i]$$$, which are swapped with a smaller element of type $$$\texttt{B}$$$.
- There are no two consecutive elements of type $$$\texttt{B}$$$. Proof: if you swap $$$[j, i]$$$, $$$p_{j-1}$$$ (if it exists) must be of type $$$\texttt{A}$$$ (otherwise $$$[j-2, i]$$$ is swappable).
- The elements of type $$$\texttt{A}$$$ are increasing. Proof: it's true if no $$$\texttt{B}s$$$ become $$$\texttt{A}s$$$, and it's also true if some $$$\texttt{B}s$$$ become $$$\texttt{A}s$$$ because any of them is adjacent to two $$$\texttt{A}s$$$.
After the operation $$$2.i$$$:
- The three properties above are still true.
- The suffix $$$[i, n]$$$ contains the values in $$$[i, n]$$$ in order. Proof: $$$a_i$$$ is an $$$\texttt{A}$$$, so it must be the largest $$$p_i$$$ in $$$[1, i]$$$, which is $$$i$$$.
Now let's understand how we can implement the algorithm. Example implementation:
- We maintain a segment tree. The $$$i$$$-th position of the segment tree contains information about the element which was initially $$$p_i$$$. Note that the relative position of $$$\texttt{B}s$$$ never changes: for example, if you want information about the last $$$k$$$ $$$\texttt{B}s$$$ in the current permutation, and you search them in the segment tree, you will find exactly the last $$$k$$$ $$$\texttt{B}s$$$, even though their indices will not correspond to the current indices.
- We have to find the longest swappable subarray ending at $$$i$$$. It means we need the current positions of the $$$\texttt{B}s$$$. For each $$$\texttt{B}$$$ maintain the current position, and assume the position of all the $$$\texttt{A}s$$$ is $$$0$$$. Also maintain, for each element, if it is a $$$\texttt{B}$$$ or not. Note that the $$$\texttt{B}s$$$ that are affected by each operation can be found in a suffix of the segment tree.
- In this way, finding the longest swappable subarray can be done with a binary search on the segment tree: since $$$\texttt{B}s$$$ cannot be consecutive, you have to find the longest suffix such that the sum of the positions of the $$$\texttt{B}s$$$ is the maximum possible (i.e., if there are $$$k$$$ $$$\texttt{B}s$$$ and the last of them is in position $$$i$$$, the sum of their positions must be $$$k(i-k+1)$$$).
- After finding the longest subarray in the segment tree, you have to perform the operation on it, i.e., subtract $$$1$$$ from all the nonzero positions.
- Some $$$\texttt{B}s$$$ may become $$$\texttt{A}s$$$. How to detect them? Since $$$\texttt{A}s$$$ never become $$$\texttt{B}s$$$, a $$$\texttt{B}$$$ becomes $$$\texttt{A}$$$ after it is swapped with all the elements greater than it on its left. So you can precompute the number of swaps that every $$$\texttt{B}$$$ needs to become $$$\texttt{A}$$$, and put it in the segment tree as well. Again, the operation is "subtract $$$1$$$ from a range".
- Detecting $$$\texttt{A}s$$$ means detecting elements which need $$$0$$$ swaps to become $$$\texttt{A}s$$$. You can find them after each operation by traversing the segment tree (which must support "range min" on the number of swaps needed), and set their position to $$$0$$$ and the number of swaps needed to $$$\infty$$$.
Complexity: $$$2n-3$$$ moves, $$$O(n \log n)$$$ time.
1909I - Short Permutation Problem
Author: TheScrasse
Full solution: errorgorn
Preparation: TheScrasse
Insert the elements into the permutation in some comfortable order.
Suppose $$$m$$$ is even. You can insert elements in the order $$$[m/2, m/2 - 1, m/2 + 1, m/2 - 2, \dots]$$$.
You can solve for a single $$$m$$$ with DP. Can you calculate the DP for multiple $$$m$$$ simultaneously?
The first part of the DP (where you insert both "small" and "big" elements) is the same for each $$$m$$$ (but with a different length), and for the second part (where you only insert "small" elements) you don't need DP.
The second part of the DP can be replaced with combinatorics formulas.
Binomials are compatible with NTT.
Let's solve for a single $$$m$$$. Suppose $$$m$$$ is even. Start from an empty array, and insert the elements in the order $$$[m/2, m/2 - 1, m/2 + 1, m/2 - 2, \dots]$$$. At any moment, all the elements are concatenated, and you can insert new elements either at the beginning, at the end or between two existing elements.
- When you insert an element $$$\geq m/2$$$, the sum with any of the previous inserted elements is $$$\geq m$$$.
- Otherwise, the sum is $$$< m$$$.
So you can calculate $$$dp_{i,j} =$$$ number of ways to insert the first $$$i$$$ elements (of $$$[m/2, m/2 - 1, m/2 + 1, m/2 - 2, \dots]$$$) and make $$$j$$$ "good" pairs (with sum $$$\geq m$$$).
You can split the ordering $$$[m/2, m/2 - 1, m/2 + 1, m/2 - 2, \dots]$$$ into two parts:
- small and big elements alternate;
- there are only small elements.
For the second part, you don't need DP. Suppose you have already inserted $$$i$$$ elements, and there are $$$j$$$ good pairs, but when you will have inserted all elements you want $$$k$$$ good pairs. The number of ways to insert the remaining elements can be computed with combinatorics in $$$O(1)$$$ after precomputing factorials and inverses (you have to choose which pairs to break and use stars and bars; we skip exact formulas because they are relatively easy to find).
If you rearrange the factorials correctly, you can get that all the answers for a fixed $$$m$$$ can be computed by multiplying two polynomials, one of which contains the $$$dp_{i,j}$$$, where $$$i$$$ is equal to the length of the "alternating" prefix. NTT is fast enough.
Complexity: $$$O(n^2 \log n)$$$











Thanks for the fast editorial!
del
Wrong.
gcd * 2?Wrong (I tried it)
Sort the array and take the GCD of the difference of consecutive elements, then multiply it by 2.
AC Submission : 238522780
I think we need not sort the array, directly taking GCD of absolute value of difference of consecutive element , then multiplying by 2, will be sufficient.
Oh, it's ok
gcd tried it its wrong
Hi I also saw a code of gcd*2
Can you explain the proof/intuition of gcd*2?
Wrong for case :
4
4 8 12 16
5
1000 2000 7000 11000 16000
You have to check for all the powers of 2, i.e. 2, 4, 8, 16, 32 ... Proof lies in the bitmasking
Thanks for the quick editorial. I will probably become expert in this round. Thanks.
why do i see ur username in red and gradmaster on ur profile .. is it the problem with everybody else
Because of the Christmas gift.
oh
Can someone explain why this solution receives TLE? I assumed that the time complexity would simply be O(nlogn): 238557809
That's because you've used
instead of
The first one works in $$$O(n)$$$ and the second one in $$$O(log\;n)$$$ where $$$n$$$ is the size of the set. This is due to the fact that the first function is a generic function that works with any container and is guaranteed to work in $$$O(log\;n)$$$ only if the container supports random access (std::set doesn't support random access), while the second one is a specific function designed only for sets and is guaranteed to have good complexity. You can refer to the documentation in case you're confused:
This one if for the generic upper_bound
This one if for the set-specific upper_bound
Ah, unfortunate. Thanks for the insight!
I have basically the same code and I did use
r.upper_bound, but I still get TLE: 238528720. Did I perhaps get constant factored?I think I did get constant factored :( Instead of storing the segment in a
vector<pair<int, int>>, I removed this intermediate step and stored the length of the interval in avector<int>directly and it passed 238595993. I don't understand why this would impact the time factor; I thought this would only cost a bit more memory.https://codeforces.me/blog/entry/70237
I think to find upper bound on set r, you should use r.upper_bound(x), not upper_bound(r.begin(), r.end(), x)
I Feel so stupid for not getting B in an hour
MathForce. All problems have math tags.
idk why but pinely and codeton rounds are biased towards number theory and maths
Great round. Thanks for fast editorial
238549718 why does my soln of B work?
I have a different solution for H so I'll leave it here.
Let's assume $$$N$$$ is even. Consider $$$N$$$ operations $$$(1,N),(2,N-1),(1,N),\cdots,(2,N-1)$$$. These operations reverse the whole permutation. For odd $$$N$$$, one can do similar operations.
During this reversing process, every pair of numbers become adjacent at some moment. Therefore we can "insert" adjacent-swap operations to achieve the arbitrary-swap operation in the final array.
The pitfall is that when we try to do multiple arbitrary swaps, they can interfere with each other during the reversing process. However, if the target permutation has a matching structure, there are no worries about interference.
Then, remember that we can obtain any permutation by composing two appropriate matching permutations. Therefore by repeating the reverse-and-swap process twice one can sort the input permutation.
The time complexity is $$$O(N)$$$ and it's better than the intended solution. However, the number of moves is $$$3N+const$$$ and it's worse than $$$2N$$$. I'm so glad that the author didn't ask me to optimize this constant. (By the way, I'm wondering if it's possible to achieve a better constant factor with my approach.)
I solved B ..By getting gcd of all v[x]-v[x-1] and multiply it by 2can you explain ,thank you
first, every number % gcd would be same.
second, if every number % (gcd * 2) would be same, then gcd will not be gcd, it should be at least 2 * gcd.
can u pls explain in detail
for example,
7 10 16the gcd of the difference is
3So we know that after mod
3, they will be same. i.e.1 1 1If we look at
gcd * 2, i.e.6. we can see the result would be1 4 4. There could be only two elements in it. Also, if everything are still the same, then we must be have a wronggcdin the first step.got that tnx!!
But how u got intuition of that solution
can you help me understand, why taking the gcd of difference works ?
if a mod m == b mod m==c then a-b of all must have gcd as m
proof:a=km+c and b=k1m+c==>a-b ==factor of m that means a-b must have m as factor ..it must be also greatest because of the greatest common divisor
nice explanation I want to add that this rule will help in understanding this approach
if a % k == b % k then (a-b)%k==0Yes,
This property is nicely applied in 1826B - Lunatic Never Content question if anyone is interesting in using this property to practice a task
its not correct
it works when you do the GCD of the Difference Arrays only as mentioned in the main comment
Oh I thought I made it clear. The gcd in my comment means the gcd mentioned in mostafaabdelaal_03's comment, which is the gcd of the difference.
Can you provide a case?
Hello, Sorry if my doubt sounds dumb but I agree that everynumber%(gcd*2) won't be the same but how can you claim that those "not same" %(gcd*2)s will be "same" as there have to be exactly 2 numbers one would be those who are still %(gcd*2)==0 and the other ones who are not zero but how can you claim that the other ones who are not zero will be equal
let's say every number mod
gcdisx, i.e.a[i] = x + num * gcdfor some integernumthen everything mod
2 * gcdwould be eitherx, orx + gcd.This is because when
numis even,a[i] % (2 * gcd)would be stillx,when
numis odd,a[i] % (2 * gcd)would bex + gcdUnderstood! Thanks for your time
i was trying a similar approach but got stuck...please explain
+1
This blew my mind.
In problem D, when we are doing operations on a[i]and want to make it to "tar". You are just doing partitioning. Won't there be cases where we partition a[i] into y, a[i]+k-y, and then recursively do operations on both of them?
Think about adding operation as ratios, and I can spread the total sum among all of the buckets I produce (from that ai) however I want.
The amount of effort that went into this round is insane, the timeline doesn't really do it justice. Kudos to TheScrasse for never settling on anything less than perfect, and errorgorn for coordinating this extremely demanding set. This turned out to be one of the most quality rounds in my recent memory!
Thanks a lot for the solution of problem H! It's my favorite problem in this contest, but I don't deserve the merit because you've solved it :)
That makes two of us for the favourite problem part. =) Coming up with a concept this interesting is surely worth of the problemsetter's merit. I was glad to contribute, and had much fun thinking about this excellent problem some more.
Thank you very much for fast Tutorial! I dream of seeing an analysis of the problem D. Thank you for this good round!
How to solve F1 with combinatorics?
A way to think of this is to maintain the invariant that the difference of p between consecutive elements in front of the ith element is correct and also to satisfy the current consecutive difference. Denote unallocated elements smaller than i as k.
If we want to make a consecutive difference of 2, we must assign the current largest element in previous k-1 vacant place, and place any of other k-1 element in current place which is (k-1)*(k-1) ways. Note that placing the current largest element in front of ith element will not break the difference invariant.
If we want to make a consecutive difference of 1, we can either put the current largest in the previous k-1 vacancy or place any of current k element in current place. This results in 2k-1 ways. As mentioned before, placing the current largest element in front of ith element will not break the invariant.
can someone please explain first three lines of solution of problem D ?
let's forget array and assume that we have to deal with single element.
if this element is greater than k say (k+x),now in one operation we have to find 2 number a,b such that a+b=(k)+(k+x), to reduce complexity of question we are doing this trick
a+b=(k)+(k+x)=>(a-k)+(b-k)=(0)+(x)we don't care about final number we care about how many operation so we reduce all number by k so our operation changed in select number and break it such in two number such that sum is our x((k+x)-(k)).
in short after reducing by k we don't have to deal with k;)
All the problems were great and overall the contest was very enjoyable to solve. Thank you for such a good round!
Worst contest for me so far. Didnt solve any. For who wants to see pure pain:
a countertest for 238559680?
Consider cases where x = 0.
If a special point is at x = 0, y = 1, what does your logic do? What is it supposed to do?
Story timeline of the round was something new and quite interesting, I enjoyed it.
You didn't participate
In question C I have a test case : 5 1 2 3 6 7 3 4 5 7 8 1 2 3 4 5 in which many got answer 14 and 18. according to me answer is 18 as 14 is not possible please comment on it.
Will it be added to the system tests and the final standing will differ or will be ignored? TheScrasse
That test case is invalid because the endpoints are not distinct.
I was trying to find some cheaters of contest and found this...
In the editorial of problem D(solution section),
Shouldn't it be "replace y with x+y" instead of "replace x with y+z"
B in O(n): $$$\large 2^{ctz((a_1 \land \cdots \land a_n)\oplus(a_1 \lor \cdots \lor a_n))}$$$
238596786
Can anyone explain the concept behind problem D.I didnt understand the editorial
+1
Assume we create a new board $$$B$$$, on which for each number $$$x$$$ written on our original board (call it $$$A$$$), we write the number $$$x - k$$$ on $$$B$$$. Then, let's try seeing what our operation does. So, since $$$y + z = x + k \implies (y - k) + (z - k) = (x - k)$$$ (for the original board), and since we've written $$$y - k, z - k$$$ on our modified board instead of $$$x - k$$$, this gives the observation that on $$$B$$$, our operation just corresponds to replacing $$$x^{*}$$$ by two numbers $$$y^{*}, z^{*}$$$ such that $$$x^{*} = y^{*} + z^{*}$$$. Then, solving this reduced problem is pretty easy (for implementation purposes, just subtract $$$k$$$ from each element of $$$a$$$, and do the calculations on that itself).
Thanks for explaining.
spoilers make the whole text unreadable
writing complexity at the end of an editorial is cringe
problem B was really something...
it was easy
can u explain editorial?
well it is kind of obvious intuition you get once u see 2 distinct values modulo some k you think of 2 since only two values are possible however then you remmeber all values might be pair hence there is only one value and then this amazing idea gets to u about the next power of 2 which is 4 well since the numbers were allwith the same parity they have only 2 values possible (pair numbers possible values are 2 or 4 and impairs values are 1 and 3) and then again there is possiblity that they all have same value time to check 8 again only 2 values are possible, you can conlcude that the sol requires checking all powers of 2,genius,see this much easier than what the editorial makes it look like.By the way i just guided you trough how the logical thinking went in my brain
TheScrasse How does the grader for H work?
Link to comment
(Nvm, this is wrong if you run it on a decreasing array.)
By the way, isn't the number of moves for the editorial solution actually bounded above by $$$3n/2$$$? Since the number of moves during the second phase is at most the number of Bs after the first phase, which is at most $$$n/2$$$ due to there being no two consecutive Bs and the last letter being an A.
Also curious about these:
Were you aware of a solution to H that made $$$3n$$$ operations before the contest? Or did the limits just happen to be large enough to allow that to pass?
What was the original solution to H with $$$O(n\log n)$$$ operations?
H with $$$O(n \log n)$$$ operations sounds like a considerably more boring problem, as I believe you can simply simulate merge sort: suppose the right part starts at $$$x$$$, then you can use operations on $$$[x-1,x]$$$, $$$[x-2, x+1]$$$ etc to create a train of moving elements from right to left, and you remove elements from the train when they reach their final positions.
Other than the very annoying implementation, H with $$$O(n)$$$ operations is a work of art :)
Hm, I don't fully understand.
By merge sort, do you mean that given two sorted arrays on consecutive ranges, you can merge them into one sorted array?
If you do operations on $$$[x-1,x], [x-2,x+1], [x-3,x+2], \dots$$$ then this will move some elements right to left over $$$x$$$ and others left to right over $$$x$$$. But how are you removing elements when they reach their final positions? What if there's some element in the middle of the train that you don't want to keep moving?
Here's how I did it: imagine inserting just the rightmost element $$$a_i$$$ of the left half with $$$[x - 1, x]$$$ operations. $$$a_{i - 1}$$$ can trail behind two positions away for free simply by extending the segments to the left (skipping the first one). We stop the trail early if $$$a_{i - 1}$$$ doesn't need to go that far, and proceed to $$$a_{i - 2}$$$. Final case is if $$$a_{i - 1}$$$ needs land next to $$$a_i$$$, in which case we add one more swap at the end to achieve that.
I agree about $$$a_i$$$ and $$$a_{i-1}$$$, but what if $$$a_{i-2}$$$ and $$$a_i$$$ need to keep moving to the right but you don't want $$$a_{i-1}$$$ to keep moving to the right?
It's true that $$$a_i$$$ must move at least as far right as $$$a_{i-1}$$$, but once you take into account the fact that $$$a_{i-1}$$$ must trail two spaces behind $$$a_i$$$ to move them rightward at the same speed, this is no longer true.
For $$$a_{i - 2}$$$ we can forget what $$$a_i$$$ does, and focus on operations moving $$$a_{i - 1}$$$. Since they don't want to swap, the same logic keeps applying.
Can somebody please explain why my solution of problem C — Heavy Intervals does not work
In test case
l=[1,2,3],r=[10,12,13],c=[1,1,100]it's best to pair (3,10)*100, but in your solution c=100 is multiplied by 10Very well written editorial! Excellent hints that actually do help a lot if we don't want to see the full solution. Thank you TheScrasse for the good contest and the great editorial.
problem D is very nice!
The subtasks of F is helpful for some but also misleading many participants including me :(
anyways, good problems and good contest
In E, I only understand this phrase in the statement after reading editorial:
It's my fault to not read it properly, and couldn't think that it is possible to press all buttons
Can someone please prove this If ai mod k=x , one of the following holds:
ai mod 2k=x ; ai mod 2k=x+k ; problem B
I know this is old but I'm writing this for me and for any one trying to understand in the future
the second case will only happen if ai == 1k+r and not 2k+r or 3k+r ......
r means the reminder (its denoted as x in the editorial)
so when we use 2k then our reminder will be 1k+r
B was such a good question. Was stuck on the gcd approach for a while before realizing the pattern in the bits.
Check my submission,i had different implementation you might find what you are looking for
Alternative solution for E:
Let's call a subset $$$S$$$ of pressed buttons good if at the end at most $$$\left \lfloor \frac{n}{5} \right \rfloor$$$ lamps turned on. For $$$n \leq 19$$$, the amount of such subsets is $$$\leq 1159$$$. We can find them for each $$$n \in [1, 19]$$$ in $$$O\left(\sum\limits_{n=1}^{19} 2^{n} \cdot n \log n\right)$$$, and then check only them for each $$$n \leq 19$$$ testcase in $$$O(nm + 1159n)$$$.
Actually, you can prove that the number of such subset for $$$n = 19$$$ is exactly $$$\binom{19}{3} + \binom{19}{2} + \binom{19}{1} = 1159$$$ since we can think of each switch $$$i$$$ associated with a vector $$$v_i \in \mathbb{Z}_2^{19}$$$ and all the vectors are independent, so $$$v_1$$$, $$$\dots$$$, $$$v_{19}$$$ is the basis, and we only care when $$$\oplus_{j = 1}^k v_{i_j}$$$ has less than or equal to $$$3$$$ bits on (excluding the case it is equal to zero), so we get the above result.
In problem D could we have solved for the smallest x in x*k+ Sum of Ai which is divisible by x+n
Consider the case $$$A = [1, 2, 3].$$$ In this case $$$x = 0$$$ is the best choice, which is incorrect.
For only positive $$$x$$$ values, consider $$$A = [10, 10, 20]$$$ and $$$k = 10$$$. In this case smallest $$$x$$$ is $$$2$$$ that satisfies the condition, but you can't really make all numbers equal.
Can anyone help me with a simple test case for which my submission is wrong for C? It's the same logic as the above solution
https://codeforces.me/contest/1909/submission/238575783
In problem C, making small intervals is not the same as sorting the sequences of left and right endpoints and pairing the corresponding indices. Let, $$$u = L_1,L_2,...,L_n$$$ si obtained after sorting $$$l_1,l_2,...,l_n$$$ and $$$v = R_1,R_2,...,R_n$$$ is obtained after sorting $$$r_1,r_2,...,r_n$$$. Then the new intervals will be $$$[L_1,R_1], [L_2,R_2],...,[L_n,R_n]$$$.
what are you trying to say ? can you explain a little more ?
What is the difference between the approach explained in the editorial and my approach?
Your approach fails for $$$l = [1, 2]$$$, $$$r = [3, 4]$$$, $$$c = [1, 2]$$$. You claim that it's optimal to keep everything as it is, while the editorial makes $$$l = [1, 2]$$$, $$$r = [4, 3]$$$, $$$c = [1, 2]$$$ ($$$3$$$ is matched with the closest $$$l_i$$$, which is $$$2$$$). The picture "explains" why the second solution is better than the first.
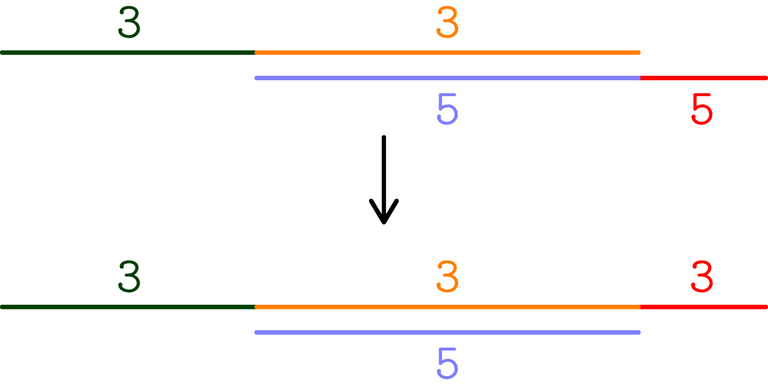
Hi, I didn't understand the picture can you explain it once? what is the 3 and 5 and what the different colors represent
The red subinterval is the only one whose cost changes (from $$$5$$$ to $$$3$$$). In general, you want intervals with big cost to be as small as possible, so you let intervals with small cost "steal" subintervals from intervals with larger cost.
In problem E, What the following line does inside the
check(int s)function of Jiangly's code 238527503if (s >> u[i] & ~s >> v[i] & 1)If button $$$i$$$ is pressed, then
s>>iwill be $$$1$$$. This line is to check whether $$$m$$$ pairs are satisfied.Thanks for interesting tasks.
Little comments for authors. problems $$$B, D, F$$$ are really cool, because they can be solved without any algorithms with only a brilliant idea.
Problem $$$C$$$. Maybe it was better to make more samples, because there were a lot of WA's and a lot of greedy solutions can pass example tests(but of course incorrect).
Problem E is kind of funny.I tried to use complicated graph algorithms but failed.And the official solution is cool!I love it!
I have another solution for problem G. It is easier than the intended one in my opinion, at least idea-wise.
Let $$$d = m - n$$$. Fix any valid $$$x$$$, $$$y$$$ and $$$z$$$. Let's see what is going on closely. If $$$i = |x|$$$ then the substring $$$t[i, i + d)$$$ is $$$y^{k-1}$$$. In particular, it has period $$$|y|$$$ and for at least $$$|y|$$$ indices $$$j$$$, starting from $$$i$$$, the equality $$$t_j = t_{j+d}$$$ holds (because another occurrence of $$$y$$$ follows $$$t[i, i + d)$$$). Obviously, the opposite works: if, for some $$$i$$$ and $$$l$$$, the substring $$$t[i, i+d)$$$ is $$$t[i, i + l)$$$ repeated several times, and for all $$$j$$$ such that $$$i\leq j < i + l$$$ we have $$$t_j = t_{j+d}$$$, then this pair $$$(i, l)$$$ corresponds to a unique valid triple $$$x = t[0, i) = s[0, i)$$$, $$$y = t[i, i + l) = s[i, i + l)$$$, $$$z = s[i + l, n)$$$. We are going to find the number of valid $$$l$$$ for each $$$0\leq i\leq n$$$. The plan is the following.
First, we find for how many first indices $$$j$$$ from $$$[i, i + d)$$$ the equality $$$t_j = t_{j+d}$$$ holds. This can be done for all $$$i$$$ in one iteration over string $$$d$$$ from right to left. Denote this number by $$$c$$$ (stands for common).
After we established this, we will find the smallest $$$p$$$ (stands for period) such that $$$t[i, i + d)$$$ is $$$t[i, i + p)$$$ repeated $$$d/p$$$ times. Then the number of good $$$l$$$ for this $$$i$$$ will equal the number of $$$g$$$ such that $$$p\mid g\mid d$$$ and $$$g\leq c$$$, or, equivalently, the number of $$$g\leq c/p$$$ for which $$$g\mid d/p$$$.
To find the period $$$p$$$, we will try to find it under the assumption that $$$p\leq d/2$$$, and if we fail, then $$$p = d$$$.
Let's solve a subtask: given string $$$u$$$ of length $$$d$$$, find its period if it's at most $$$d/2$$$. Let $$$i$$$ and $$$j$$$ be any pair of integers that $$$0\leq i$$$, $$$j\leq d$$$ and $$$j - i = \lfloor d / 2 \rfloor$$$. Then the period is $$$\min(d, \mathrm{lcm}(\mathrm{tailperiod}(u[0, j)), \mathrm{tailperiod}(u[i, d))))$$$, where $$$\mathrm{tailperiod}(v)$$$ is the smallest $$$p$$$ such that $$$v$$$ is a prefix of the infinite concatenation of $$$v[0, p)$$$ with itself (it is like a period, except there may be some leftover, although also consistent with the periodicity). The proof is left as an exercise for the reader.
To always have such pair of indices, let's find such periods for all $$$t[i, j)$$$ where $$$i$$$ is divisible by $$$\lfloor d/2 \rfloor$$$ and $$$j-i \leq d$$$. We can find them by running z-function for each substring starting at such $$$i$$$ of length $$$d$$$ (or till the end of $$$t$$$, whichever is shorter). Similarly, we can run z-function on similar substrings of $$$t$$$ reversed, which concludes this part of the solution.
What remains is to be able to tell how many divisors of $$$g\mid p$$$ don't exceed some $$$c$$$, where $$$p\mid d$$$. I just generated all divisors for each $$$p\mid d$$$ beforehand, and solved this subtask using
lower_bound. I suspect that it can be shown that $$$p$$$ in these queries first only decreases, then only increases, in which case we can re-generate the divisors every time it changes, which will be better than $$$\log$$$ per query.In D,
"Now, the operation becomes "replace x with y+z such that x+y=z+k⟹(x′+k)+(y′+k)=(z′+k)+k⟹x′+y′=z′ ". Therefore, in the shifted problem, k′=0" .I think it should be y+z = x+k instead of x+y = z+k.
Fixed, thanks.
I can understand the solution of G now,but I've got no idea about how the vital observation "$$$(a,b)$$$ is valid then $$$(a+1,b+1)$$$ is valid if and only if $$$s_{b+1}=t_{b+1}$$$" was found.What inspired you think about that?Can someone help me?
Actually, I only found it while preparing the problem (with constraints $$$n, m \leq 2 \cdot 10^5$$$). I was trying to build strong tests (where the valid $$$y$$$ of fixed length are not consecutive), but I ended up proving it's not possible.
I'm curious about how actual contestants figured it out.
Can someone explain the intution behind problem C?
https://en.wikipedia.org/wiki/Rearrangement_inequality might help
Can you explain how the rearrangement inequality is related?
I guess I actually do see how it is used in the problem (in sorting the cost array in descending order with the lengths), but that wasn't the hard part for me. The part that was hard was how to pick the elements l and r. I guess an intuitive explanation would be that you want to maximize the lengths so that you can pair a higher length with a a lower cost. To do that, for the smallest Rs, you want to pick and L that is the closest to them because you want to save the smaller Ls for the Rs that are larger, because that results in a larger lengths. I can elaborate more on this if anyone wants me to.
in problem c I'm trying to follow the editorial in the proof section he is saying at the third line If you swap ri and rj, the cost does not increase. I did that on the example n=2 provided and the cost increased from 6 to 7 first step he said match them any other order so: [2,4] [1,3] then he said You have also assigned some cost ci to [li,ri] and cj to [lj,rj] . [2,4] ci=2 [1,3] ci=1 now cost is 6 then ** If you swap ri and rj, the cost does not increase. ** swapping here will make the cost 7 so I don't get it can you please explain what is wrong here
In the editorial, $$$c_i \leq c_j$$$. If $$$c_i > c_j$$$, you have to swap $$$l_i$$$ and $$$l_j$$$.
Can someone help me to explain the complexity of problem E plz?
For each test case, you have to iterate over $$$O(n^{k-2}) = O(k^{2k-4})$$$ masks (in the worst case), and for each of them you can check if it works in $$$O(m)$$$.
I know how to prove $$$O(n)=O(k^2)$$$, but I don't know how $$$O(n^{k-2})$$$ comes out (especially $$$k-2$$$ power). Sorry for bad English expression.
tl;dr replace $$$5$$$ with $$$k$$$ and $$$3$$$ with $$$k-2$$$ in the editorial.
The largest solution to $$$\lfloor n/k \rfloor < \lfloor \sqrt n \rfloor$$$ is $$$n = k(k-1)-1$$$. In that case, you already have a solution which turns $$$\lfloor \sqrt{k(k-1)-1} \rfloor \leq k-1$$$ lamps on, so you can iterate over masks which contain $$$k-2$$$ lamps.
Thank you so much!
But here seems to be a little mistake? I suppose it should be "The largest solution to $$$\lfloor n/k\rfloor<\lfloor \sqrt{n}\rfloor$$$".
Yes, fixed.
For D, the shifting part is still unclear to me(ik what is being done ,but how is it correct and how to think of it) thnx in advance if someone can spare their time or share related resources
I was really struggling for a while to come to grips with this solution and I think I am now (mostly) convinced of why it works, so I'll try to explain my way of thinking about it.
Imagine a number line with numbers x, y and z marked such that y + z = x + k.
Now think about the operation you can do: y + z = x + k. Going back to the number line, what this operation means is you would have to pick x and move it k unities to the right, then pick two numbers x and y such that their sum "lands" in (x + k) and not x.
For each of those three numbers now, mark in the number line its value shifted k unities to the left, and call these new guys x', y' and z'. Clearly you can represent x by (x' + k), y by (y' + k) and z by (z' + k). So, looking again at our operation, we have (y' + k) + (z' + k) = (x' + k) + k -> y' + z' = x'.
What that tells us is that if we had a magical way of taking every number on our line and shifting it k unities to the left, when we would execute the operation on an original number x, instead of doing that complicated process (moving it k unities to the right and only then finding numbers which add to it), we could map x to its representation in the shifted "world" and find two other numbers, also in the shifted world, such that their sum is equal to the representation of x.
Our magical way of doing this shift is simply to take every number given in the input and subtract it by k. Now, for every operation we do in those numbers (including gcd), we are working with numbers from our shifted world; so we can now solve the problem as if k didn't even exist. Hope this is helpful in some way :)
can someone give the intuition behind the idea of "shifted problem" for D ? is it a trick or just random manipulation for this specific problem
In D you can also do the reverse problem: Start at the final state which is a bunch of identical elements then apply "combine and subtract $$$k$$$" operations and arrive at a similar solution with algebra.
problem D is amazing i have different approach for. suppose mn and mx are the max and min elements if mx == mn ans is 0. if mn <= k && k <= mx we can neve the values of array to a single value. if k < mn || k > mx ans will exist. assume at the end all the elements are equal to x so the last element we remove = 2 * x — k. second last element we would remove will be either 2 * x — k or 3 * x — k and so on. it shows that all the elements in the initial array is of the form .. pi * x — (pi — 1) * k, after rearranging pi(x — k) + k. now ans would be just summation of all pi.
Problem I is 1900!!!
TheScrasse, is it an error?
Problem I — 1900!
Ir's because of a bug of the rating system. I cannot do anything about that.
C seems to be a bit difficult for a 1400; or is it just for me?
Div1C is different difficulty than a Div4C problem even if they're both rated same.
There must be
x + 2kinstead ofx + k.For example, let
ai = 5andk = 2:5 % (2*2) = 1;Hence,
xis1.If we go with
ai % (2k) = x + k, then:1 + 2 != 5But:
1 + 2*2 == 5;TheScrasse
C was a great problem. I did it by sorting li array,and iterating it from back,now find upper_bound of each li in ri array and pair li with it. The main idea was: in any kind of arrangement sum of all (ri-li) would be same,which basically means its always better to create least posssible (ri-li) at each instant possible,so that large ci could be assigned to them and the differential gain due to large ci reduces.
Nice contest
Fast and on point editorial.
in B, Learnt that while shifting for large powers to use 1LL<<i, else shifting wont work for large powers & (1<<i) while shifting make sure it doesnt fudge with the brackets