After the World Final this year, I think that instead of let the reference material we used rot in a depository, it is better if we can collaborate and polish a piece of reference that can serve as the foundation for any team that wishes to best their skill in contests, or for any person who wishes to achieve a higher rating on Codeforces. After all, who can say that they haven't thought of "color their name red" on this website?
So here it is, Allow me to present you Luna's Magic Reference, which is the foundation we used to develop our reference for the ICPC contests last year: https://github.com/Nisiyama-Suzune/LMR
I hope that you can try to utilize it in the next contest, point out bugs or confusing parts if you find any, and share your own masterpiece of code that can potentialy benefit the whole community.
Thanks in advance and wish you all high rating!









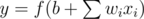
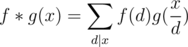
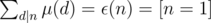 , we can also claim that
, we can also claim that 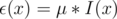 .
.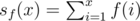 for a given
for a given 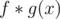 (denoted as
(denoted as 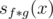 ) are (miraculously) very easy to obtain in
) are (miraculously) very easy to obtain in 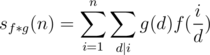
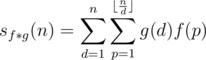
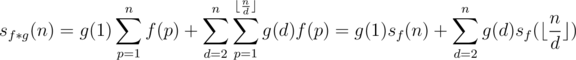
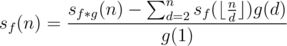
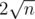 different elements exist for
different elements exist for 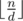 . We can thus recursively calculate the value of those
. We can thus recursively calculate the value of those  complexity.
complexity.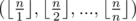 of
of 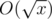 , the overall cost should be
, the overall cost should be 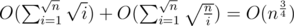 .
.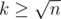 elements of
elements of 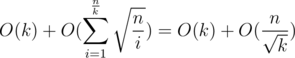
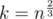
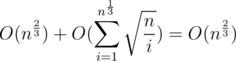
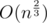 .
.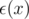 ,
, 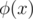 , we can prove that
, we can prove that 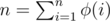 (with the "
(with the "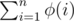 is multiplicative first, and then compute
is multiplicative first, and then compute 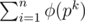 ), so
), so 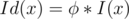 .
.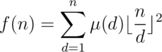
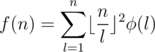
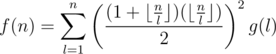
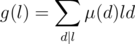
 . Therefore, if we use
. Therefore, if we use 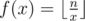 as the hashing function, we can prove that
as the hashing function, we can prove that 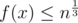 and
and  complexity (with the
complexity (with the 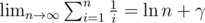 ). Let us take a minute to consider the bottleneck of such sieve. While we do need to cross out each composite once, in practice we run the inner loop for a composite multiple times due to the fact that it has multiple factors. Thus, if we can establish a unique representation for each composite and pick them out only once, our algorithm will be somewhat better. Actually it is possible to do so. Note that every composite
). Let us take a minute to consider the bottleneck of such sieve. While we do need to cross out each composite once, in practice we run the inner loop for a composite multiple times due to the fact that it has multiple factors. Thus, if we can establish a unique representation for each composite and pick them out only once, our algorithm will be somewhat better. Actually it is possible to do so. Note that every composite 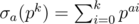 , denoting the sum of the
, denoting the sum of the 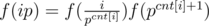 . The following code gives an example on the function I've just written.
. The following code gives an example on the function I've just written.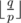 refers to the integer division.
refers to the integer division.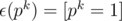 .
.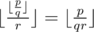 .
.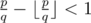 . Hence
. Hence 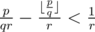 . Since the fraction part of
. Since the fraction part of 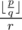 cannot exceed
cannot exceed 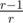 , we achieve the conclusion.
, we achieve the conclusion.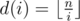 . For every
. For every  , there will be no more than
, there will be no more than 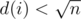 and is a positive integer, so there can be at most
and is a positive integer, so there can be at most 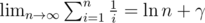 , we know that
, we know that 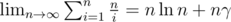 , so the sum of the original sequence is approximate to
, so the sum of the original sequence is approximate to 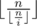 . The piece of code below demonstrates one way to program it.
. The piece of code below demonstrates one way to program it.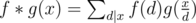 is also multiplicative. Specifically, if
is also multiplicative. Specifically, if 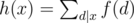 is also multiplicative.
is also multiplicative.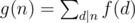 for every positive integer
for every positive integer 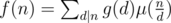 , where
, where 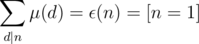
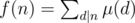 is multiplicative. After that, we can see
is multiplicative. After that, we can see 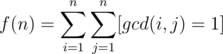
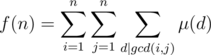
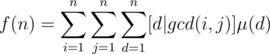
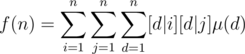
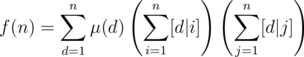
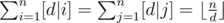 . Thus
. Thus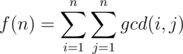
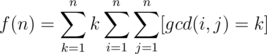
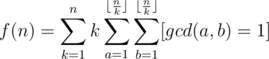
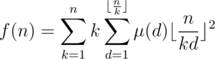
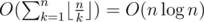 . Therefore, if we compute the sum above with brute force, the overall complexity will be
. Therefore, if we compute the sum above with brute force, the overall complexity will be 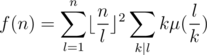
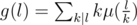 is multiplicative. Moreover, we have
is multiplicative. Moreover, we have 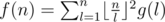 , which can be simply computed in
, which can be simply computed in 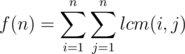
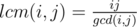 , let
, let 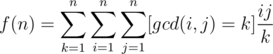
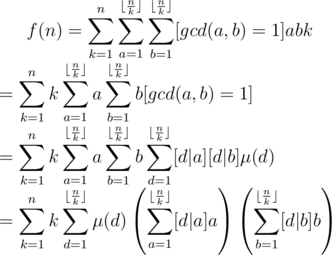
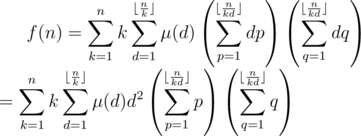
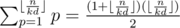 , and we have
, and we have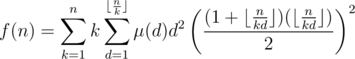
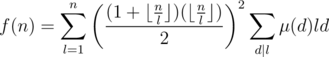
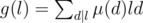 is also multiplicative, and
is also multiplicative, and 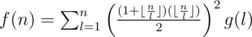 . The overall complexity will be
. The overall complexity will be 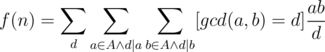
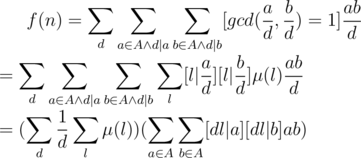
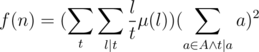
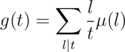 is multiplicative with
is multiplicative with  is also fairly easy to figure out if you keep track of the number of the elements equal to
is also fairly easy to figure out if you keep track of the number of the elements equal to 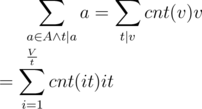
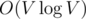 . Hence the overall complexity is
. Hence the overall complexity is 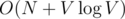 .
.
