Собственно сабж.
У меня осталась одна попытка на финал ACM-ICPC, и хотелось бы в следующем сезоне съездить и побороться за что-нибудь в финале. В связи с этим ищу команду. Если кто вдруг может чего-нибудь предложить интересного в этом плане, пишите в лс =)









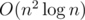 , или же
, или же 
