490A - Командная олимпиада

Будем формировать команды жадно. То есть, если у нас есть по одному школьнику каждого из трёх типов, которые ещё не относятся ни к какой команде, то из них можно сформировать новую команду. И так делее, пока достигнется ситуация, когда мы не сможем сформировать команду. Таким образом, общее число команд — это минимум из количеcтва школьников каждого из трёх типов. Решение получается за O(N), если сложить индексы школьников каждого типа в три отдельных массива. Можно решать и за O(N²), если каждый раз пробегаться по всему массиву в поисках школьника конкретного типа для очередной команды.

490B - Очередь

Эту задачу будем решать конструктивно. Определим, кто находится на первом месте — это студент с таким номером, который встречается среди чисел a_i, но не встречается среди чисел b_i (потому, что ни для кого из остальных он не находится позади). Определим, кто находится на втором месте — это студент, который стоит позади первого, а поскольку у первого студента число a_i равно 0, то соответствующее ему число b_i и будет его номером (то есть число из пары [0, b_i]).

Теперь будем определять остальных, начиная с третьего. Это делается очень просто по предпоследнему уже определенному номеру студента. Номер очередного студента, это число b_i в некоторой паре, где число a_i, это номер предпоследнего уже найденного номера студента (то есть число из пары [ans[i - 2], b_i]. Решение достаточно просто осознать, разбирая пример из условия.

490C - Взлом шифра

Будем решать эту задачу следующим образом. Сначала проверим все префиксы заданного числа — делятся ли они на число a. Это можно сделать за O(N), где N — это длина заданного числа C. Зная остаток от деления префикса, заканчивающегося в позиции pos, можно пересчитать остаток для позиции pos + 1 следующим образом: rema[pos + 1] = (rema[pos] * 10 + C[pos + 1]) % a.

Затем нужно проверить все суффиксы числа C — делятся ли они на число b. Зная остаток от деления суффикса, начинающегося в позиции pos, можно пересчитать остаток для позиции pos - 1 следующим образом: remb[pos - 1] = (C[pos - 1] * P + remb[pos]) % b, где P — это 10^(L - 1) по модулю b, L — это длина суффикса (величину P можно вычислять параллельно).

Теперь нужно перебрать все позиции pos и проверить, можно ли сделать разрез числа C после этой позиции. Для этого необходимо выполнение четырех условий: префикс числа C, заканчивающийся в позиции pos, делится на число a; суффикс числа C, начинающийся в позиции pos + 1, делится на число b; длины префикса и суффикса ненулевые; суффикс не может начинаться с цифры 0. Если все эти условия выполняются, то после позиции pos можно сделать разрез. Если же все позиции не подходят, то решения не существует и следует вывести NO.

490D - Шоколадки

Заметим, что мы можем преобразовывать число следующим образом, либо делить на два либо делить на три и домножать на два. Изначально уберём из чисел все степени двоек и троек. После этого проверим, возможно ли удалив все эти степени добиться равенства площадей, если нет, то ответа не существует. Посмотрим на разность количества троек в факторизации шоколадок. Понятно, что именно на такое число нужно сократить одну из шоколадок, в зависимости от знака. Выполним данную операцию, пересчитывая количество двоек, и после сделаем то же самое для них.

490E - Восстановление возрастающей последовательности

Будем решать данную задачу жадным образом. Будем перебирать заданные числа сначала и пытаться сделать из текущего числа минимальное, но большее предыдущего. Обозначим текущее число — cur, а предыдущее число — prev.

Если длина числа cur меньше длины числа prev — следует вывести NO, задача не имеет решения.

Если длина числа cur больше длины числа prev — заменим все знаки ? в числе cur на цифру 0, за исключением случая, когда знак ? стоит в первой позиции — заменим его на цифру 1, так как числа в ответе не могут иметь лидирующих нулей.

Остался случай, когда длины чисел cur и prev равны. По условию задачи, каждое число в ответе должно быть строго больше предыдущего. Переберем позицию pos, в которой префикс числа cur больше чем префикс числа prev. Теперь попробуем для этой позиции сделать минимально возможное число, большее prev. Во всех позициях pos_i в которых стоит знак ? и меньших pos, поставим цифру, которая стоит в соответствующей позиции числа cur. А во всех позициях pos_i в которых стоит знак ? и больших pos, поставим цифру 0. Если в числе cur в позиции pos стоит знак ?, то поставим в эту позиции цифру на 1 большую, чем prev[pos]. Если в prev[pos] стоит цифра 9, то данная позиция pos не подходит для рассмотрения.

Если полученное число меньше либо равно предыдущему, то данная позиция pos не подходит. Из всех подходящих позиций pos выберем минимальное число, полученное в результате описанных выше действий, присвоим ему число cur и продолжим восстановление ответа. Если подходящих позиций pos на каком-то шаге не нашлось — следует вывести NO.

490F - Турне по Древляндии

Задача является обобщением нахождения наибольшей возрастающей подпоследовательности в массиве, поэтому наверняка решается диначеским программированием. Будем делать динамику d[(u, v)], в которой состоянием является ориентированное ребро в графе (u, v). В динамике будем хранить максимальное число вершин, где группа могла дать концерты на каком-то простом пути, заканчивающемся в вершине v и проходящем через вершину u. Причём в вершине v точно будет концерт.

Чтобы посчитать значение для ребра (u, v) нужно посчитать значение для всех рёбер (x, y) таких, что существует простой путь, начинающийся в вершине x, проходящий через вершины y и u и заканчивающийся в вершине v.Чтобы найти все рёбра (x, y), удовлетворяющие этому условию, нужно просто запустить обход в глубину из вершины u, которому будет запрещено заходить за вершину v. Тогда все ребра, которые он обойдёт, нужно просто взять с обратной ориентацией. Таким образом если r[y] < r[v], то d[(u, v)] = max(d[(u, v)], d[(x, y)] + 1). В итоге получется решение за O(N²) и (O(N²)) памяти. Память можно сократить до линейной если научиться получать индексы ориентированных рёбер без обращения к двумерному массиву.

435A - Очередь на остановке

Эта задача решается за один проход по всем группам. Решение можно представить следующим кодом:

int result = 1;
int people = 0;

for(int i = 0; i < n; i++)
{
    if (people + a[i] <= m)
        people += a[i];
    else
    {
        result++;
        people = a[i];
    }
}

cout << result << endl;

435B - Паша максимизирует

Эта задача решается жадно. Будем стараться максимальные цифры ставить как можно раньше. Алгоритм можно описать так:

1) Рассмотрим каждую позицию по очереди, начиная с 1, пусть текущая позиция i
2) Среди следующих k цифр числа найдем ближайшую максимальную, пусть она находится на позиции j
3) Если эта цифра больше текущей цифры на позиции i, то сделаем серию обменов, поставим ее на позицию i, одновременно умешьшим величину k, то есть выполним k = k - (j - i)

435C - Кардиограмма

Эта задача носила технический характер, нужно было реализовать описанное в условии. Для начала нужно было посчитать координаты всех точек ломанной. Также заведем матрицу для хранения ответа. Поскольку координата y могла становиться отрицательной, удобно было удвоить размеры матрицы и изначально сдвинуть картинку вверх на 1000. В конце нужно будет вывести ее без лишних пустых строк.

Чтобы нарисовать саму кардиограмму, можно было рассмотреть каждую пару последовательных точек ломанной и отдельно расставить символы в матрице ответа. Если ломаная возрастает, нужно нарисовать прямой слеш, иначе обратный. Чтобы лучше разобраться как это сделать, можно аккуратно нарисовать первый тестовый пример на листочке, отметить координаты и понять как изменяются значения по координатам (какие границы получаются у циклов в программе).

435D - Специальная сетка

Так как ограничения на n и m были не очень большие, должно было проходить решение за O(max(n, m)³), то есть перебор всех треугольников. А именно, нужно было перебрать все треугольники и проверить для каждого треугольника за O(1), что он удовлетворяет всем описанным условиям.

Чтобы быстро выполнять проверку, нужно было для всех диагоналей, строк и столбцов сохранить массив частичных сумм. И далее, проверять запросом на сумму, лежит ли в данном отрезке на соответствующей линии хотя бы одна черная точка.

Полезные соображения, помогающие значительно сократить реализацию описанного выше:

• все треугольники, которые нужно посчитать — равнобедренные прямоугольные треугольники;
• либо катеты треугольника параллельны сторонам сетки, либо гипотенуза параллельна одной из сторон сетки;
• если научиться решать задачу, считая, что нужно посчитать количество треугольников только двух видов, то решение для всех треугольников можно получить, посчитав ответы для 4-х поворотов матрицы.

435E - Специальный граф

Для того, чтобы решить последнюю задачу, нужно было порисовать различные раскраски на листочке бумаги. Далее путем исследований установить, что бывает два вида корректных раскрасок: вертикальные и горизонтальные.

Вертикальные раскраски выглядят следующим образом:

acbcbd...
bdadac...
acbcbd...
bdadac...
acbcbd...
bdadac...
......

Другими словами, каждая вертикаль содержит только два цвета, вертикали одной четности содержат одинаковые цвета. При этом очередность цветов на каждой вертикали может быть совершенно произвольная.

Горизонтальные раскраски выглядят аналогично, только повернуты на 90 градусов. Конечно, бывают раскраски, которые одновременно и горизонтальные и вертикальные, но для решения задачи, это не имеет никакого значения.

Давайте научимся проверять, существует или нет, корректная вертикальная раскраска, удовлетворяющая шаблону заданному во входных данных. Это достаточно просто. Достаточно просто перебрать, какие цвета и на каких вертикалях находятся. А затем проверить, что такую раскраску действительно можно составить.

Аналогично нужно проверить для горизонтальных раскрасок.

Сложность решения O(n × m).

Всем привет)

Уже завтра в привычное время состоится очередной раунд Codeforces #249 для участников Div. 2. Участников Div. 1 мы традиционно приглашаем поучаствовать в этом соревновании вне конкурса.

Задачи для вас вновь готовили авторы Павел Холкин (HolkinPV) и Геральд Агапов (Gerald). Как всегда, мы выражаем свою благодарность Михаилу Мирзаянову (MikeMirzayanov) за прекрасные системы Codeforces и Polygon, а также Марии Беловой (Delinur) за перевод условий задач.

UPD: Распределение баллов по задачам будет стандартным — 500-1000-1500-2000-2500.

Желаем всем участникам удачи, высокого рейтинга и удовольствия от решения задач)

UPD2: соревнование завершилось, надеемся оно вам понравилось)

UPD3: ссылка на разбор уже здесь)

UPD4: Поздравляем победителей!:

1) JiangZemin_JiangHaha
2) Rafbill
3) Yukinoshita_Yukino
4) kuangbin9
5) spartacus

432A - Выбор команд

В этой задаче нужно было посчитать количество студентов, которые еще могут участвовать в ACM ICPC, поделить его на три и округлить вниз. Это можно сделать так:

int cnt = 0;

for(int i = 0; i < n; i++)
    if (5 - a[i] >= k)
        cnt++;

int ans = cnt / 3;

432B - Футбольная форма

Посчитаем для каждой команды количество матчей в домашней форме. Для команды i это количество равно сумме числа всех домашних n - 1 игр и гостевых игр с такими команды, у которых цвет домашней формы совпадает с цветом гостевой формы команды i. Чтобы посчитать количество таких гостевых игр, можно заранее предпосчитать количество команд с определенным цветом домашней формы. Итоговое решение будет выглядеть примерно так:

for(int i = 0; i < n; i++)
    cnt[ x[i] ]++;

for(int i = 0; i < n; i++)
{
    ans_home[i] = n - 1;
    ans_home[i] += cnt[ y[i] ];

    ans_away[i] = 2 * (n - 1) - ans_home[i];
}

432C - Простые обмены

Решение этой задачи можно описать следующим псевдо-кодом:

1. Перебираем элементы перестановки от 1 до n

2. Пока текущий элемент i не находится на позиции i

3. Пусть текущая позиция элемента i равна pos

4. Найти наибольшее простое меньшее либо равное pos - i + 1, обозначим его p

5. Поменять местами элементы в позициях pos и pos - p + 1

Можно доказать, что данный алгоритм всегда будет совершать не более 4n обменов. Проще всего это сделать, если написать код, который находит максимальное количество итераций цикла <ПОКА> для всех возможных pos - i.

Кроме всего прочего данный алгоритм нужно было реализовать оптимально. А именно поддерживать позиции элементов перестановки. В авторском решении была следующая функция:

void doSwap(int i, int j){
    int x = a[i], y = a[j];
    a[j] = x, pos[x] = j;
    a[i] = y, pos[y] = i;
    result.push_back(make_pair(i, j));
}

432D - Префиксы и суффиксы

Существует много решений этой задачи. Мы опишем решение, которое использует префикс функцию. Построим префикс функцию p строки s. Далее построим дерево, вершины которого — числа от 0 до |s|, а ребра идут из p[i] в i для каждого i. Корень дерева — это вершина 0. Далее для каждого v посчитаем сколько значений p[i] = v, обозначим его за cnt[v]. А затем для каждого v посчитаем сумму sum[v] всех cnt[u], где вершина u находится в поддереве вершины v.

Ответ на задачу считается считается следующим образом:

Найдем все длины префиксов, которые совпадают с суффиксами — это значения |s|, p[|s|], p[p[|s|]], p[p[p[|s|]]]... Для каждой такой длины L количество вхождений соответствующего префикса в строку это sum[L] + 1.

432E - Замощение квадратами

Разбор по задаче Е будет чуть позже, а пока всем понравившийся тест номер 6 :)

13 5

AAAAA
AAAAA
AAAAA
AAAAA
AAAAA
BBBBB
BBBBB
BBBBB
BBBBB
BBBBB
AAACA
AAABB
AAABB

Будем решать задачу стандартным методом — то есть будем заполнять таблицу от более значащих клеток к менее значащим. В каждую клетку будем стараться ставить букву как можно меньше.

Рассмотрим самую первую строку, понятно, что оптимальная раскраска этой строки начинается с нескольких букв A. На самом деле букв A в начале этой строки должно быть min(n, m). Поставив нужные буквы A в эту строку, мы должны поставить буквы A и в другие строки, чтобы образовать квадрат. Следующая буква (после закраски первого квадрата из A) в первой строке может быть только B.

Попробуем построить более общий алгоритм решения задачи. Предположим, что мы уже рассмотрели несколько строк, и теперь рассматриваем строку i. Вполне вероятно, что в нашей таблице в строке i некоторые клетки уже закрашены. Будем итерироваться по незакрашенным клеткам в порядке слева направо. Для каждой клетки будет перебирать ее цвет от A до Z. Нужно рассмотреть два случая:

1. Поставить в текущую клетку наименьшую букву, такую, что в соседних клетках нет такой буквы.

2. Если предыдущая клетка в строке была свободна на момент начала покраски i-й строки, то мы ее уже покрасили в какой-то цвет. Нужно попробовать объединить текущую клетку с квадратом, в котором находится предыдущая клетка.

Из двух описанных вариантов нужно выбрать тот, в котором цвет клетки получается меньше. Чтобы лучше понять, как должен работать алгоритм разберите его работу на примере n = 13 m = 5

Доброго времени суток, codeforces)

Приглашаем вас на очередной раунд Codeforces #246 для участников Div. 2. Как всегда, участники Div. 1 могут поучаствовать в этом соревновании вне конкурса.

Задачи для вас готовили авторы Павел Холкин (HolkinPV) и Геральд Агапов (Gerald). Уже не первый и, определенно, не последний раз мы стараемся для вас. Традиционно мы говорим слова благодарности Михаилу Мирзаянову (MikeMirzayanov) за прекрасные системы Codeforces и Polygon, а также Марии Беловой (Delinur) за перевод условий задач.

UPD: Распределение баллов по задачам будет стандартным — 500-1000-1500-2000-2500.

Желаем всем участникам удачи и удовольствия от решения задач)

UPD2: Соревнование завершилось, надеемся оно вам понравилось)

UPD3: А вот и ссылка на разбор задач

Поздравляем победителей!:

1) PopovkinAndrey
2) FTD2009
3) Gulan14no
4) Kozakai_Aya
5) Mikael

413A - Восстановление данных

Посчитаем минимум и максимум в заданном массиве размера m. Если минимум уже меньше заданного min, либо если уже максимум больше заданного max, то ответ Incorrect.

Посчитаем минимальное значение 0 ≤ need ≤ 2, которое будет равняться числу элементов, которые надо добавить в исходный массив, чтобы его минимум стал равен min, а максимум стал равен max. Для этого нужно попарно сравнить минимум заданном массиве со значением min и максимум в заданном массиве со значением max. Тогда ответ Correct, если n - m ≥ need. Иначе ответ Incorrect.

413B - Spyke чат

Обработаем все запросы и будем поддерживать следующие величины: для каждого сотрудника будем поддерживать число сообщений, которые он отправил в какой-нибудь чат и для каждого чата количество сообщений, которые были отправлены в этот чат. Тогда ответ для каждого сотрудника — это сумма числа сообщений, отправленных во все чаты, участником которых является данный сотрудник, минус число сообщений которые отправил сам сотрудник в какой-нибудь чат.

413C - Своя игра

Для начала выберем все вопросы не аукционы и ответим на них. Затем у нас останутся только вопросы аукционы. Отсортируем их по неубыванию стоимости. Далее переберём минимальный размер суффикса, вопросы из которого нужно будет взять за их стоимость, а остальные вопросы возможно будет использовать для умножения нашего выигрыша на 2.

Очевидно, что это наиболее выгодно, поскольку чем меньше стоимость вопроса, тем меньше нужно иметь очков для умножения своего баланса на 2. Так же чем больше стоимость вопроса, тем более выгодно брать его за реальную стоимость.

413D - 2048

Рассмотрим произвольное состояние в нашей игре. Заметим, что нам имеет смысл поддерживать максимальный по длине суффикс чисел в убывающем порядке. При этом будем хранить только младшие k - 1 степень двойки, а также запомним была ли уже достигнута k-ая степень или выше. Действительно, если убывающий порядок нарушился, то мы никогда не сможем использовать эти числа, поскольку значения могут только увеличиваться.

Поэтому посчитаем следующую динамику dp[i][mask][j], где i — размер уже рассмотренного префикса элементов, а mask — маска размера k, в которой бит x возведён тогда и только тогда, когда среди последних идущих по убыванию степеней двойки присутствует 2^x, j — была ли уже достигнута k-ая степень или выше (0 или 1). Возможны два типа переходов, когда пришло число 2 и когда пришло число 4. Если пришло число 0, то выполним оба перехода.

413E - Лабиринт 2D

Будем обрабатывать запросы по очереди. Вначале проверим, достижима ли одна клетка из другой. Для этого вначале найдем компоненты связности. Если клетки находятся в разных компонентах связности, то ответ -1.

Иначе предположим, что обе клетки находятся в столбцах, в которых ровно одно препятствие. Чтобы найти длину пути между ними, необходимо предподсчитать с помощью частичных сумм длины путей между такими столбцами.

Для этого пройдем по столбцам слева направо, поддерживая тип последнего столбца с одним препятствием (препятствие в нижней строке, либо препятствие в верхней строке). Если в столбце j тип препятствия изменился, то запишем в массив для частичных сумм в позицию j единицу, иначе запишем ноль. Тогда ответ на такой вид запросов будет равен сумме модуля разности столбцов клеток запроса и значения посчитанной частичной суммы между ними.

Если столбец с левой клеткой запроса не содержит препятствий, то найдем ближайший справа от него столбец с одним препятствием, а для столбца с правой клеткой запроса найдем ближайший слева столбец с одним препятствием. Таким образом, мы сведем общий вид запроса к описанному выше. Нужно быть аккуратным в случае, если между клетками запроса нет столбцов с ровно одним препятствием.

382A - Ксюша и чашечные весы

В этой задаче нужно было совсем немного техники программирования. Можно было брать свободные гирьки по одной и добавлять на ту чашу весов, где сейчас меньше гирек. После этого требовалось просто вывести ответ в правильном формате.

382B - Разрушители чисел

В этой задаче нужно было понять, что из себя представляет хитрая операция Артура. На самом деле, если перед выполнением всех действий сделать присвоение b = w - b - 1 (то есть как бы перевернуть ситуацию), то операция аналогична присвоению b = (b + x) % w. Причем если происходит переполнение через w, то дополнительно происходит присвоение a = a - 1.

Таким образом, если выполнить k таких операций, то переменные изменятся так: b = (b + k·x) % w, a = a - (b + k·x) / w, c = c - k. Зная это, легко решить задачу бинарным поиском по ответу.

382C - Арифметическая прогрессия

В этой задаче нужно было разобрать несколько несложных случаев:

1) если n = 1, то ответ: -1, потому что любые два числа будут являться арифметической прогрессией;
2) если массив состоит целиком из одного числа, то ответ: эта единственная константа;
3) если вам уже дана арифметическая прогрессия, то ответ это 2 числа: minVal - d, maxVal + d, где minVal — минимум, maxVal — максимум, d — разность прогрессии.
Однако, если n = 2, то в этом случае ответ бывает 3 числа (как, например, в последнем тестовом примере, когда разность (a[1] - a[0]) четна);

4) иначе, возможно, в прогрессии пропущено ровно одно число и его можно аккуратно найти двигаясь по исходному массиву (предварительно его удобнее отcортировать). Разность прогрессии можно вычислить, как d = min(a[i + 1] - a[i]) (если n > 2);
5) во всех иных случаях ответ 0;

382D - Ксюша и пешки

В этой задаче из всех клеток кроме # один переход. Поэтому граф на клетках является почти фунцкиональным графом. Если в этом графе есть цикл, то очевидно ответ -1, потому что этот цикл имеет длину не менее 2 и мы можем разместить на нем две наши пешки.

Иначе в графе нет циклов. Найдем в нем самый длинный путь, пусть его длина len. Тогда если мы расположим две наши пешки в первую и вторую клетку пути, то ответ на задачу уже будет 2·len - 1.

Однако, иногда можно получить ответ 2·len, если в этом графе есть два непересекающихся по вершинам пути (вершины, не являющиеся #). Непересекающиеся они будут потому, что если вдруг они пересеклись в какой-то клетке, то дальше они будут совпадать (а по условию задачи такие ходы совершать нельзя).

Остается проверить есть ли в этом графе два непересекающихся по вершинам (не #) пути длины len. Это можно сделать как угодно. Например, посчитать для каждого истока v величину d[v] длины пути из него. После серией поисков в глубину из всех истоков с максимальным d[v] = len проверить найдутся для два непересекающихся пути. (если очередной поиск в глубину не находит поюзанной вершины, значит этот путь новый).

382E - Ксения и комбинаторика

Чтобы решить задачу, нужно было посчитать количество деревьев с заданными свойствами. Сделать это можно с помощью динамического программирования. Основная идея динамического программирования в том, что размер максимального паросочетания в дереве ищется простой линейной динамикой dp[v][used] (v —- вершина, used —- уже использована она в паросочетании или нет), поэтому для подсчета количества деревьев достаточно включить в состояние динамики два значения dp[v][0] и dp[v][1].

Другими словами, нужно написать динамику z[n][dp0][dp1], значение которой — это количество подвешенных деревьев, состоящих из n вершин, в корне которых динамика dp[root][0] = dp0, а dp[root][1] = dp1. Если просто написать такую динамику она будет получить TL по времени. Из этого положения можно выйти двумя способами. Либо посчитать все значения динамики прекалком, немного оптимизировав код, либо ассимптотически оптимизировать динамику.

Авторское решение использует второй подход. Для того, чтобы оптимизировать динамику достаточно заметить, что значение dp0 отличается от значения dp1 не больше чем на 1. То есть либо dp0 = dp1, либо dp0 = dp1 + 1. Тогда динамика превращается в динамику r[n][dp0][add], которая работает сильно быстрее. Другая важная оптимизация состоит в том, что возможных троек (n, dp0, add), для которых значение r[n][dp0][add] ненулевое очень мало (около 250). Это значит, что достижимых состояний динамики не много, поэтому если написать ее "лениво" с отсечениями, программа будет работать в несколько раз быстрее.

Комментарии, которые описывают решения (некоторые отличаются):

http://codeforces.me/blog/entry/10423#comment-158177
http://codeforces.me/blog/entry/10423#comment-158182

Всем доброго времени суток)

Приглашаем вас на очередной раунд Codeforces #224 для участников Div. 2, первый Div2 Only в новом 2014 году:) Как обычно, участники Div. 1 могут поучаствовать в этом соревновании вне конкурса.

Задачи для вас готовили авторы Павел Холкин (HolkinPV) и Геральд Агапов (Gerald). Уже давно сбился со счета в скольких раундах я принимал участие в качестве автора, соавтора или просто активного помощника) Традиционно мы говорим слова благодарности Михаилу Мирзаянову (MikeMirzayanov) за отличные системы Codeforces и Polygon, а также Марии Беловой (Delinur) за перевод условий задач.

UPD: Распределение баллов по задачам будет динамическим, однако задачи будут расположены в предполагаемом порядке возрастания сложности. Первый динамический раунд в этом году)

Желаем всем участникам удачи, высокого рейтинга и удовольствия от решения задач)

UPD2: соревнование завершилось, надеемся оно вам понравилось) разбор задач уже здесь)

Поздравляем победителей:

1) tankmagiciangirl
2) NagaiNatsuyasumi
3) lijian3256
4) TankKiller
5) dashabi

342A - Ксюша и делители

В этой задаче нужно было догадаться, что существует только 3 корректные тройки:

1) 1, 2, 4

2) 1, 2, 6

3) 1, 3, 6

Будем жадно набирать их пока получается. Если остались какие то неиспользованные числа (в том числе 5 и 7, которые очевидно сразу являются плохими), то выведем -1. Иначе выведем найденный ответ.

342B - Ксюша и шпионы

Эта задача решается жадно. Будем всегда двигаться только по направлению от s до f. Причем, если в данный момент можно совершить действие, обязательно будем его совершать. Иначе не будем передавать записку соседу и оставим ее у себя (такой ход можно делать в любой ситуации). Очевидно, что такой подход приводит к правильному решению, остается его аккуратно реализовать.

342C - Шкаф и шарики

В задаче нужно было аккуратно выписать формулу. Оптимальное решение укладывает шарики по два в ряд, пока это возможно. А потом сверху кладет еще один шарик, если это возможно. Основная хитрость и сложность была именно в последнем шаге.

В комментариях к посту были описаны формулы, как узнать, уместится ли в самом конце один шарик (в самую середину). А также был приведен красивый рисунок, который хорошо иллюстрирует ситуацию .

342D - Ксюша и доминошки

В этой задаче можно было как считать количество хороших расстановок, так и из общего числа вычесть плохие расстановки. В любом из решений нужно было уметь считать динамику по маскам, состояние (j, mask) — j — номер текущего полностью заполненного столбца, mask — маска того, что находится в последнем столбце (также этот прием называет динамикой по профилю). Это по сути известная задача о паркете (замощения поля доминошками). Как решать классическую задачу о паркете, можно узнать на известном сайте e-maxx.ru.

Чтобы получить само решение задачи я поступал так. Пробовал к клетке с кружочком приписывать с четырех сторох доминошку, после этого все три клетки закрашивал в черный цвет и считал общее количество способов. Однако, чтобы не учитывать один ответ несколько раз, нужно использовать формулу включения исключения для этих четырех направлений. Это также известный прием, который позволяет правильно считать ответ для многих задач и не учитывать один ответ несколько раз.

342E - Ксюша и дерево

Задачу можно было решать несколькими методами. Самый простой из них — корневая оптимизация. Разобьем запросы на sqrt(m) блоков. Каждый блок будем обрабатывать отдельно. Перед тем как обработать блок одним обходом в ширину посчитаем кратчайшие расстояния от красных вершин до всех остальных. Далее, чтобы выполнить запрос на вывод ответа из текущего блока нужно взять значение полученное обходом в ширину и обновить его расстояниями до красных вершин из текущего блока, которые покрасились до текущего запроса.

Решение получается очень простым. Каждые sqrt(m) запросов запускаем обычный поиск в ширину и запоминаем для каждой вершины значение d[v] — кратчайшее расстояние от нее, до ближайшей красной. После этого, чтобы ответить на запрос типа 2, нужно взять min(d[v], dist(v, u)), где u — каждая новая красная вершина, которая стала красной именно в этом блоке длины sqrt(m).

Расстояния между вершинами dist(u, v) на дереве можно было считать, используя предпосчет для lca.

Доброго времени суток)

Приглашаем вас на очередной раунд Codeforces #199 для участников Div. 2. Как обычно, участники Div. 1 могут поучаствовать в этом соревновании вне конкурса.

Задачи для вас готовили авторы Павел Холкин (HolkinPV) и Геральд Агапов (Gerald). Традиционно выражаем благодарность Михаилу Мирзаянову (MikeMirzayanov) за системы Codeforces и Polygon, а также Марии Беловой (Delinur), которая перевела условия задач.

UPD: Распределение баллов по задачам будет стандартным — 500-1000-1500-2000-2500.

Желаем всем участникам удачи, высокого рейтинга и удовольствия от решения задач)

UPD2: итак соревнование завершилось, надеемся вам понравилось)

Поздравляем победителей:

1) chixianglove
2) Logvinov_Leon
3) Yoshiap
4) _moonlight

UPD3: разбор задач можно найти здесь

292A - SMS-центр

Для каждого момента i времени запомним количество сообщений z[i], которое нужно отправить в момент времени i. Теперь пройдем по каждому моменту времени от 1 до 10⁶, поддерживая текущий размер очереди sz. На каждой итерации попробуем уменьшить размер очереди на 1, то есть выполним sz = max(sz - 1, 0), затем прибавим сообщения, которые нужно отправить в эту секунду, то есть выполним sz = sz + z[i]. На каждом шаге будем обновлять максимальное значение очереди и текущее время, если sz > 0. После выполнения цикла, если в очереди остались неотправленные сообщения, то нужно еще раз обновить ответ.

292B - Топология сети

В этой задаче нужно было посчитать степени каждой вершины и найти ответ. Замечу, поскольку n >  = 4, m >  = 3 и граф связный, то ответ однозначный.

1) все степени 2 и у двух вершин степень 1 — шина.
2) все степени 2 — кольцо
3) все степени 1 и у одной степень  > 2 — звезда
4) иначе неизвестно

292C - Красивые IP-адреса

Задача решается перебором. Для начала переберем сколько цифр в каждом четверти мы возьмем, например AAA.B.CC.DDD. Теперь посчитаем количество символов в этой строке (AAABCCDDD) и переберем цифры на первой половине этой строки (поскольку строка должна быть палиндромом, то вторая половина однозначно восстанавливается). После этого проверим, что такой ip-адрес является корректным и содержит правильный набор цифр. Если ip-адрес удовлетворяет всем условиям задачи, то добавим его к ответу.

292D - Компоненты связности

Ограничения в задаче были не слишком удачными и провоцировали писать решение за квадрат, мы постарались максимально не позволить таким решениям пройти.

У этой задачи много правильных решений. Изначально планировалось решение, которое предподсчитывает частичные dsu (структура данных disjoint set union) на префиксах и на суффиксах, то есть массивы ldsu[M][N] и rdsu[M][N]. После этого на запрос [lf ; rg] легко ответить за время O(N·A^- 1), если объединить множества ldsu[lf - 1] и rdsu[rg + 1], где A^- 1 -- обратная функция Аккермана (константа от dsu).

292E - Копирование данных

У этой задачи много правильных решений. Изначально предполагалось решение, использующие корневую эвристику. Разобьем все запросы на sqrt(m) блоков. Будем поддерживать текущий массив b в виде отрезков в массиве z, который хранит четверки (lf, rg, type, start), где lf, rg — отрезок индексов массива b, type — 0 или 1, означающее из какого массива взяты числа для этого отрезка, start — позиция начала этого отрезка в массиве типа type.

На запросы будем отвечать в тупую, то есть честно пересчитывать как изменится массив z от запроса копирования и отвечать на запросы значения в позициях. Однако, каждые sqrt(m) запросов будем сливать данные из массива z в массив b, для того чтобы сам массив z сильно не разрастался.

Есть простое решение с деревом отрезков, которое умеет делать покраску на отрезке. Пусть пришел запрос копирования [lf ; rg], , тогда покрасим отрезок запроса [lf ; rg] в цвет, равный номеру запросу. Все запросы будем сохранять. Пусть пришел запрос значения в позиции x, тогда найдем цвет в дереве в этой позиции. Если такого цвета нет, значит мы находимся в исходном массиве b (выведем b[x]), иначе посчитаем смещение dx от начала этого запроса до нашей позиции x и выведем a[x + dx].

Доброго времени суток)

Совсем скоро стартует Раунд 1 Всероссийского Открытого Чемпионата по программированию "КРОК-2013". Из в Раунда 1 в следующий Раунд 2 проходят участники, набравшие не меньше баллов, чем участник на 400-ом месте (при условии положительного числа набранных баллов).

Раунд будет проходить по обычным правилам Codeforces (со взломами и падением стоимостей задач). Во время раунда задачи тестируются системой только на претестах, а системное тестирование состоится после окончания соревнования. Претесты не покрывают все возможные случаи входных данных, поэтому тщательно тестируйте свои программы.

До окончания раунда категорически запрещается публиковать где-либо условия задач/решения/какие-либо мысли и соображения о них. Запрещено общаться на тему задач, обсуждать условия, решения и прочее.

Задачи для вас подготовила команда авторов в составе: Павел Холкин (HolkinPV), Геральд Агапов (Gerald) и Михаил Мирзаянов (MikeMirzayanov). Отмечу, что команда в этом же составе провела для вас квалификационный раунд и отвечала на вопросы в течении всего соревнования. Традиционно благодарим Марию Белову (Delinur), которая перевела для вас условия задач.

UPD1: Задачи будут расположены в порядке возрастания предполагаемой сложности. Распределение баллов было решено сделать немного нестандартным: 1000, 1000, 1500, 2000, 2500.

UPD2: в связи с большим количеством участников было решено, что в соревновании нельзя будет участвовать вне конкурса. Для официальных участников соревнование будет рейтинговым.

Всем участникам желаем удачи и успешного прохождения в следующий раунд соревнования.

285A - Немного убывающие перестановки

В качестве ответа можно было предложить такую перестановку: n, n - 1, ..., n - k + 1, 1, 2, ..., n - k. Например, если n = 5, k = 2, то ответ: 5, 4, 1, 2, 3. Если k = 0, нужно вывести 1, 2, ..., n. Такое решение можно написать в два цикла.

285B - Найди шарик

Известно, что перестановку можно представить в виде множества циклов. Число i переходит в число p[i] для всех i (1 ≤ i ≤ n). Можно было начать двигаться из стартового числа s по циклу до тех пор, пока мы не дойдем до конечного числа t, либо же не вернемся назад в s. Если мы вернулись в начало, нужно вывести  - 1, иначе вывести длину пути.

285C - Получаем перестановку

У этой задачи решение очень простое. Нужно отсортировать последовательность a, а затем первое число свести к числу 1, второе к числу 2, и так далее. Число a[i] добавит к ответу величину |a[i] - i|. Ответ нужно считать в 64-битном типе данных.

Почему это решение верно? Разумеется, до этого легко догадаться. Чтобы в этом убедиться, попробуем это показать методом от противного. Рассмотрим, например, числа x, y, z. Пусть x < y < z и мы хотим свести число x к числу z вместо числа y. Однако, после некоторого количества операций  + 1 число x окажется равным y. После этого можно считать, что мы будем сводить первоначальное число y к числу z, а первоначальное число x к числу y. То есть, сведение числа x к числу z было равносильным по количеству операций. Различные подобные рассуждения приводят к решению, описанному выше.

285D - Сумма перестановок

Опишем сначала переборное решение. Во-первых, всегда будем считать, что перестановка a тождественная, то есть a[i] = i. В таком случае, полученный ответ просто домножим на n!. В противном случае ваш перебор не досчитается. Во-вторых, с помощью нашего перебора заметим, что для четных n ответ равен 0.

Что теперь нужно сделать, чтобы сдать задачу. Первый вариант — это посчитать на вашем компьютере все ответы и записать их в константый массив, иначе говоря сделать прекалк. Вариант второй — пытаться ускорять ваше решение. Решение, использующее подход meet-in-the-middle успевает для n ≤ 15. Поскольку для четных n ответ 0, то такое решение также проходит. С другой стороны, другие простые переборы и динамики на map-ах в 3 секунды не уложились.

285E - Позиции в перестановке

Доброго времени суток, друзья)

Приглашаем вас на очередной раунд Codeforces #175 для участников Div. 2. Как обычно, участники Div. 1 могут поучаствовать в этом соревновании вне конкурса.

Задачи для вас вновь готовила группа авторов в следующем составе: Павел Холкин (HolkinPV), Артем Рахов (RAD), Фефер Иван (Fefer_Ivan) и Геральд Агапов (Gerald). Как всегда благодарим Михаила Мирзаянова (MikeMirzayanov) за системы Codeforces и Polygon, а также Марию Белову (Delinur), которая перевела условия задач.

Распределением баллов публикуем заранее) cегодня оно будет стандартным: 500, 1000, 1500, 2000, 2500.

Откроем небольшой секрет этого соревнования, сегодня во всех задачах вы столкнетесь с перестановками)

Надеемся, что соревнование окажется для вас удачным, желаем всем высокого рейтинга, успешных взломов и хорошего настроения)

UPD1: соревнование завершилось, надеемся оно вам понравилось)

UPD2: разбор задач уже можно найти здесь)

UPD3: поздравляем победителей:

1) hechuan
2) TroyI118
3) BekzhanKassenov
4) ahmed_aly
5) lxgsbqylbk

Привет, друзья)

Уже скоро состоится очередной раунд Codeforces #171 для участников Div. 2. Как всегда, участники Div. 1 могут поучаствовать в соревновании вне конкурса.

Вновь и вновь для вас старалась уже знакомая группа авторов в составе: Павел Холкин (HolkinPV), Игорь Кудряшов (Igor_Kudryashov), Николай Кузнецов (NALP) и Геральд Агапов (Gerald). Традиционно хотим поблагодарить Михаила Мирзаянова (MikeMirzayanov) за системы Codeforces и Polygon, а также Марию Белову (Delinur) за перевод условий задач.

UPD: распределение баллов по задачам будет немного нестандартным: 500, 1000, 1500, 2000, 2000.

Надеемся, что соревнование окажется удачным для всех участников. Мы желаем всем высокого рейтинга, успешных взломов и хорошего настроения)

UPD2: соревнование завершено, надеемся оно вам понравилось)

Поздравляем победителей:

1) study_english
2) ipip2005
3) rng_50216
4) bfrcns197
5) csavky103

UPD3: разбор задач можно найти здесь

Доброго времени суток, друзья)

Через несколько часов состоится очередной раунд Codeforces #166 для участников Div. 2. Как всегда, остальные могут поучаствовать в соревновании вне конкурса.

И вновь для вас старалась группа авторов: Павел Холкин (HolkinPV), Николай Кузнецов (NALP), Артем Рахов (RAD) и Геральд Агапов (Gerald). Традиционно хочется поблагодарить Михаила Мирзаянова (MikeMirzayanov) за системы Codeforces и Polygon, а также Марию Белову (Delinur) за перевод условий задач.

UPD: Распределение баллов будет немножко нестандартным — 500, 1000, 1500, 2000, 3000.

Надеемся, что соревнование окажется удачным для всех участников. Желаем высокого рейтинга, успешных взломов и хорошего настроения)

UPD2: соревнование завершилось, надеемся оно вам понравилось)

Поздравляем победителей:

1) xrvpud221
2) xyz111
3) nanoha
4) wyx528
5) GuyUpLion

UPD3: разбор задач уже опубликован, его можно найти здесь

266A - Камни на столе

В этой задаче нужно было посчитать количество пар подряд идущих одинаковых букв. Это можно сделать в один цикл за время O(N).

266B - Очередь в школе

В этой задаче нужно было аккуратно реализовать процесс, описанный в условии. Нужно было t раз обменять два элемента i и i + 1 местами, если на i-ом месте стоял мальчик, а на i + 1-ом стояла девочка. Главное, не нужно было одну девочку двигать влево несколько раз за одну итерацию. Решение можно реализовать за O(N·T).

266C - Ниже диагонали

Эту задачу будем конструктивно, даже скорее используя индуктивный подход. В начальный момент у нас есть квадратная матрица размера n и n - 1 единица в ней. Следовательно, существует столбец, в котором нет ни одной единицы. Поставим этот столбец на n-ое место. Таким образом, правый нижний элемент будет равен 0. Теперь найдем любую строку, в которой есть хотя бы одна единица, и поставим ее на n-ое место.

Мы добились того, что в клетке (n, n) стоит 0, а также в последней строке стоит хотя бы одна единица. После этого можно уменьшить размерность задачи, то есть n:  = n - 1. Заметим, что в этой задаче у нас будет не более n - 2 единиц, следовательно эту задачу решить аналогичным образом. Когда n окажется равным 1, алгоритм нужно завершить, поскольку в первой строке будет 0 единиц. Всего у нас получается O(N) операций swap, не более двух для каждого n.

266D - БерДональдс

Расскажу несколько идей решения этой задачи. Сначала предложим решение за O(N⁴). Переберем ребро (u, v) длины len, на котором окажется точка из ответа. Пусть эта точка находится на этом ребре на расстоянии x от вершины u. Тогда расстояние до любой другой вершины i равно min(x + d[u][i], len–x + d[v][i]), где d[x][y] — расстояние между вершинами x и y. Приравняем эти величины, посчитаем критическое значение величины x для вершины i, получим x = (len + d[v][i]–d[u][i]) / 2. Отсюда видно, что ответ на задачу полуцелый. Таким образом, для каждого ребра и для каждой вершины получим набор таких критических точек. Проверим каждую из них помимо самих вершин графа (границы отрезка). Возможно такое решение вполне реально сдать, добавив какие-нибудь оптимизации или идеи.

Также можно было решать задачу за O(N³·log²). Умножим веса всех ребер на 2. Теперь переберем ребро, на котором находится ответ и сделаем бинарный поиск по ответу (уже в целых числах). Чтобы проверить текущий ответ, нужно перебрать вершину i, считая что ответ достигается в этой вершине. Тогда получим, что точка на этом ребра должна лежать либо <= какого-то l[i], либо >= какого-либо r[i]. Эта подзадача решается в оффлайне с помощью сортировки событий и поддержания баланса.

Также можно было попытаться сдать тернарный поиск на каждом из ребер графа. Однако, поскольку в чистом виде он работает неправильно, нужно было разбить ребро на некоторое количество отрезков и искать на каждом из них.

Последние два решения проходили, если их аккуратно реализовать. Еще отмечу, что также есть решение за время O(N³) автора задачи RAD.

266E - Опять запросы к массиву...

Эта задача решается с помощью структуры данных. Будем использовать дерево отрезков, причем будем поддерживать k деревьев отрезков для каждой из степеней. В вершине будем поддерживать взвешенную сумму с соответствующей степенью, а также число, которое означает цвет всего отрезка, если такой есть.

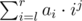Пользователь Egor в комментариях к посту, а также пользователь mexmans в комментариях к разбору, описывали свои формулы для получения ответа. Постараюсь объяснить как их можно получить. Во-первых нужно выписать, что умеет в качестве запроса считать ваше дерево отрезков. Оно умеет получать сумму . Вам же нужно посчитать 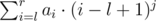, можно записать как 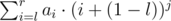. Теперь нужно расписать на листочке последнюю сумму для первых степеней, хотя бы до трех, и отнять из первой суммы (ответ на запрос дерева) вторую (то что нужно получить). Получится выражение, которое нужно вычесть из числа запроса для получения ответа на задачу. Это просто бином Ньютона без старшей степени.

Таким образом, ответ для степени j выражается как разность числа запроса и бинома Ньютона со всеми степенями, которые меньше j (эти значения также можно запрашивать вашим деревом отрезков). Частичные суммы степеней и сочетания нужно заранее предпосчитать. Решение имеет сложность O(N·K·log(N)).

Всем привет)

Сегодня состоится очередной раунд Codeforces #163 для участников Div. 2. Как обычно, остальные могут поучаствовать в нем вне конкурса.

Задачи для вас подготовили авторы: Артем Рахов (RAD), Кудряшов Игорь (Igor_Kudryashov), Павел Холкин (HolkinPV) и Геральд Агапов (Gerald). Традиционно хочется поблагодарить Михаила Мирзаянова (MikeMirzayanov) за систему Codeforces, а также Марию Белову (Delinur), которая перевела условия задач.

UPD: В раунде будет использована динамическая система оценки задач. Задачи отсортированы, по мнению авторов, по предполагаемому порядку увеличения сложности.

Надеемся, что соревнование окажется удачным для всех участников. Желаем высокого рейтинга и хорошего настроения)

UPD2: соревнование завершилось, надеемся оно вам понравилось)

Поздравляем победителей:

1) Aharon

2) marcoskwkm

3) ChaosLogic

4) Imsbuno

5) Conny

UPD3: разбор задач можно найти здесь)

Всем привет)

Сегодня состоится очередной раунд Codeforces #161 для участников Div. 2. Как и всегда, остальные могут поучаствовать в нем вне конкурса.

Задачи для вас подготовили авторы: Павел Холкин (HolkinPV), Николай Кузнецов (NALP) и Геральд Агапов (Gerald). Традиционно хочется поблагодарить Михаила Мирзаянова (MikeMirzayanov) за систему Codeforces и возможность проведения соревнований. Также благодарим Марию Белову (Delinur), которая перевела условия задач. Также выражаем благодарность Артему Рахову (RAD) и Виталию Аксенову (Aksenov239) за помощь в проведении соревнования.

UPD: В раунде будет использована динамическая система оценки задач. Задачи отсортированы, по мнению авторов, по предполагаемому порядку увеличения сложности.

Надеемся, что соревнование окажется удачным для всех участников, успешных взломов и высокого рейтинга)

UPD2: соревнование завершилось) надеемся оно вам понравилось

Поздравляем победителей:

1) poao900
2) persianpars
3) Sert
4) valentin.harsan10
5) MeinKraft

UPD3: разбор задач опубликован, его можно найти здесь

260A - Добавление цифр

Сначала попробуем приписать справа любую цифру от 0 до 9, которая подойдет под условие задачи. Если это не получится, сразу выведем -1. В противном случае остальные n–1 можно сделать 0, так как делимость от этого не пропадет.

260B - Древнее пророчество

В этой задаче нужно было перебрать все даты от 2013 до 2015 года (високосных годов среди них нет), посчитать количество вхождений каждой даты в исходную строку и найти максимум. В году 365 дней, следовательно это решение за (3·365·N).

260C - Коробки и шарики

Сначала опишем простой способ получения решения. Будем по одному шарику доставать из коробок, начиная с коробки x справа налево (действие назад). В какой-то момент в текущей коробке окажется 0 шариков. Это коробка является начальной для нашей исходной задачи, то есть та, откуда мы взяли все шарики и начали раскладывать. Тогда в эту коробку положим число шариков, равное количеству шариков, которое мы только что достали из всех коробок.

Только так задачу решать нельзя, потому что это количество может быть очень большим. Заметим, что прежде чем столкнуться с этой ситуацией, мы несколько раз пройдем по всему массиву и вычтем 1. Поэтому этот процесс можно ускорить, предварительно убрав из каждой коробки, например, minv - 1 шарик, где minv — минимум в исходном массиве. После этого останется выполнить O(N) указанных выше простых операций.

260D - Черно-белое дерево

Задачу будем решать конструктивно, поддерживая следующий инвариант — сумма значений белых вершин равна сумме значений черных вершин. Дерево является двудольным графом, поэтому построим в качестве ответа двудольный граф без циклов, который будет удовлетворять условиям задачи. Долями будут являться черные и белые вершины.

На каждом шагу будем выбирать вершину v с наименьшей суммой из белых и черных. После этого найдем любую вершину u противоположного цвета и проведем ребра (u, v) веса s[v], а из суммы вершины u вычтем сумму вершины v, то есть s[u] = s[u]–s[v]. Будем продолжать этот процесс, пока не он не закончится. Циклов в графе не получится, потому что каждый раз, обнуляя очередную вершину, будем ее удалять. В какой-то момент может оказаться, что мы удаляем последнюю вершину одного из цветов. Поскольку мы поддерживаем инвариант равенства сумм черных и белых, оставшиеся вершины нужно просто присоединить к графу любым корректным образом с весом ребра 0.

260E - Разделение королевства

Переберем 9! способов расположений чисел a[i] по 9 областям. Зафиксировав некоторое положение, то есть некоторую решетку, легко посчитать количество городов левее левой вертикальной прямой, правее правой вертикальной прямой, ниже нижней горизонтальной прямой и выше верхней горизонтальной прямой. Каждое из этих значений есть сумме некоторых трех значений a[i].

Будем считать, что прямые из ответа всегда проходят по полуцелым координатам. Тогда, зная указанные выше 4 числа, можно однозначно определить отдельно по x и y, как должны расположиться все 4 прямые. Остается лишь только проверить, что во всех областях нужное количество точек.

Для каждой из четырех зон (левее левой вертикальной прямой, правее правой вертикальной прямой, ниже нижней горизонтальной прямой и выше верхней горизонтальной прямой) отдельно проверим, что все три области этой зоны содержат нужное число точек. Это будет делать при помощи сканирующей прямой и дерева отрезков, которое умеет искать сумму на отрезке и делать обновление в точке. Для этого сложим все эти запросы в некоторый массив, отсортируем и будем обрабатывать слева направо. Заметим, что проверив 8 условий из 9 для каждого из 9! расположения решетки, центральную область проверять не нужно, она восстановиться сама собой. Если ни одно положение не подойдет, нужно вывести -1.

Всем доброго времени суток)

Новый год уже на носу, а тем временем мы рады приветствовать вас на очередном раунде Codeforces #158 для участников Div. 2, быть может последнем в уходящем году). Как обычно, участники Div. 1 могут поучаствовать вне конкурса.

Задачи для вас были подготовлены авторами: Николай Кузнецов (NALP), Фефер Иван (Fefer_Ivan), Павел Холкин (HolkinPV) и Геральд Агапов (Gerald). Традиционно хочется поблагодарить Михаила Мирзаянова (MikeMirzayanov) за систему Codeforces и Polygon, а также Марию Белову (Delinur), которая перевела условия задач.

Распределение баллов по задачам будет стандартным.

Всем участникам соревнования успешных взломов, высокого рейтинга и удачи в новом году!

UPD: соревнование завершилось, надеемся оно вам понравилось)

Поздравляем победителей:

1) ballmaids01
2) betalife37
3) showtime
4) vlyubin
5) bardek

UPD2: разбор задач опубликован, его можно найти здесь)

246A - Неудачная сортировка

В этой задаче нужно было взломать сортировку, разумеется приведенный алгоритм был неправильным. Однако он верно работал для массивов длины n <  = 2. В остальных случаях можно было привести в качестве контр-примера последовательность n, n–1, ..., 1. Чтобы исправить данную сортировку, нужно во втором цикле бежать не от i, а от 1.

246B - Прибавляй и умешьшай

Заметим, что с помощью приведенной операции всегда можно получить n–1 одинаковое число. Для этого будем всегда приравнивать первые n–1 чисел, а n-ое число будем произвольно уменьшать или увеличивать вместе с ними. Однако после приведенных действий весь массив может оказаться равным. Это происходит в том случае, если сумма всех элементов делится на n. Таким образом, в данной задаче ответ либо n, либо n–1.

246C - Конкурс красоты

Данная задача была скорее математической. Правильным решением в ней является следующий выбор: сначала возьмем все n элементов по разу, затем возьмем максимальный элемент и вместе с ним произвольный, затем два максимальных и с ними произвольный, затем три максимальных и произвольный и так далее. Всего получится ровно столько наборов, сколько требовалось в условии. Нетрудно проверить, что все суммы окажутся различными.

246D - Цветной граф

Данную задачу можно решать так: построим новый граф, вершинами в котором будут являться цвета исходного графа. Ребро между двумя вершинами u и v будет в том случае, если в исходном графе существует ребро, соединяющие вершины a и b такие, что c[a] = u и c[b] = v. Тогда ответом на задачу является такой цвет k, минимальный по номеру, что степень вершины k в новом графе максимальна (без учета кратных ребер). Такое решение можно реализовать за O(M·log(N)).

246E - Братья по крови возвращаются

Задача была немного похожа на задачу 208E - Братья по крови. В комментариях к той задаче было описано решение при помощи структуры deque (массив, в который можно добавлять и удалять элементы с обеих сторон). Теперь применим эту структуру в этой задаче.

Для начала все различные имена переведем в различные числа и для каждой вершины v запомним, какие запросы у нее были. Далее для каждой вершины, которая является корнем некоторого дерева запустим dfs, в качестве параметров передадим ему вершину v и deque< set > z. Этот deque будет для каждой глубины i в поддереве вершины v хранить set — различные имена (числа) на глубине i.

Пересчитать его просто. Посмотрим на всех сыновей вершины v и посчитаем для них такой же deque. Очевидно, что размер нашего deque z будет максимальным из всех deque-ов потомков. Далее пройдем по всем deque-ам и объединим соответствующие set-ы чисел. Причем, разумеется, будем меньший set присоединять к большему. После этого нужно в начало нашего deque z вставить set размера 1 — цвет вершины v.

После этого сразу же можно ответить на запросы этой вершины. Ответ либо 0, если потомков на такой глубине нет, либо размер z[k], поскольку это как раз множество различных имен на глубине k от вершины v. Известно, что такой подход работает за хорошую асимптотику, в частности авторское решение работало около секунды. Если быть конкретнее, асимптотика решения O(N·log²(N)).

В качестве пояснения к этой задаче хочу отметить, что реализовывать ее нужно аккуратно. Нужно избегать копирований deque-ов и set-ов. Нужно делать swap меньшего и большего set-a или deque-а без копирования всех элементов, а затем всегда меньший присоединять к большему.

Всем доброго времени суток)

Рады приветствовать вас на очередном раунде Codeforces #151 для участников Div. 2. Как обычно, остальные могут поучаствовать в нем вне конкурса.

Задачи для вас были подготовлены авторами: Павел Холкин (HolkinPV) и Геральд Агапов (Gerald). Традиционно хочется поблагодарить Михаила Мирзаянова (MikeMirzayanov) за прекрасную систему Codeforces и Polygon, а также Марию Белову (Delinur), которая перевела условия задач.

Распределение баллов по задачам будет стандартным.

Всем участникам соревнования мы желаем удачи, успешных взломов и высокого рейтинга!

UPD: контест завершен, надеемся вам понравилось)

Поздравляем победителей:

1. a58 (решивший все 5 задач)
2. thangpc
3. Minecraft
4. xiaoshua3
5. Noskov

UPD2: разбор задач можно найти здесь

228A - Не смешите мои подковы

В этой задаче нужно посчитать количество различных чисел из входных данных cnt и вывести 4–cnt. Это можно было сделать как угодно. Например, сложить все числа в сет и посчитать его размер.

228B - Две таблицы

В этой задаче нужно было аккуратно перебрать всевозможные сдвиги  - N <  = x, y <  = N, посчитать текущий ответ и найти максимум среди всех полученных. Асимптотика решения O(N⁴).

228C - Детектор фракталов

Задача решалась при помощи динамического программирования. Посчитаем динамику z[x][y][st][mask] ---является ли квадрат с верхним левым углом в клетке (x, y) фракталом уровня вложенности st, который получен исходным квадратом с цветами, обозначаемыми mask. Значение z[x][y][st][mask] хранит 0 или 1. Состояний в такой динамике O(N²·Log(N)·2⁴). Переходы в ней достаточно очевидны. Если st = 1, это означает, что нужно честно проверить квадрат размера 2*2 с верхним левым углом в клетке (x, y) на совпадение с исходной маской mask. Если st > 1, нужно разделить этот квадрат на четыре меньшие части и проверить, что для них всё выполняется. Если значение mask в одной четверти означает черный цвет, нужно проверить, что вся четверть является черной. Это можно сделать за O(1) при помощи частичных сумм на прямоугольниках. Если же четверть имеет белый цвет, нужно проверить, что она является фракталом уровня вложенности st–1 с той же маской mask. Получается не более 4 переходов из каждого состояния.

Чтобы посчитать ответ на задачу, нужно перебрать всевозможные левые верхние углы квадратов, всевозможные маски и для каждого уровня вложенности проверить, что данный квадрат нам подходит. Это и делает наша динамика.

228D - Зигзаг

В этой задаче нужно было воспользоваться тем, что последовательность s имеет циклический вид из-за своей структуры. Также было важно, что 2 <  = z <  = 6. Для каждого z выпишем последовательность s и увидим, что длина её периода 2 * (z–1).

Тогда, для каждого z и каждого модуля 0 <  = mod < 2 * (z–1) заведем отдельное дерево отрезков или фенвика, которое нам поможет отвечать на запросы. Нужно быть аккуратным с памятью, нам требуется O(Z·(2·Z)·N) памяти. Если запрос на изменение в позиции, нужно обновить z значений в деревьях с соответствующими модулями для этой позиции. Если запрос на сумму, нужно посмотреть все 2·(z–1) модулей и для каждого отдельного посчитать сумму, домножив её на нужный коэффициент, который мы берем из последовательности s. Решение имеет сложность O(Z·N·Log(N)).

228E - Как два пальца об асфальт

У этой задачи оказалось много решений. Первоначально предполагалось решение, которое решало систему равенств по модулю 2, используя алгоритм Гаусса. Расскажем другое простое решение.

Вершины, которые мы возьмем в ответ, назовем включенными. Во-первых, очевидно, что каждую вершину мы включим не более одного раза. Теперь посмотрим на произвольное ребро (x, y) цвета c. Нам нужно, чтобы его цвет в результате равнялся 1. Если c = 1, нужно либо не включать вершины x и y, либо нужно их обе включить. Если c = 0, нужно включить либо x, либо y. Таким образом, если мы рассмотрим произвольную вершину v и переберем, включим ее или нет, то можно однозначно восстановить, какие вершины придется включить в компоненте связности вершины v. Если в некоторый момент у нас возникнет коллизия, мы выбрали неправильный цвет у вершины v. Если хотя бы одну компоненту покрасить не удастся, нужно вывести Impossible. Это можно реализовать за O(N + M) серией поисков в ширину.

Всем доброго времени суток)

Рады приветствовать вас на очередном раунде Codeforces #141 для участников Div. 2. Как обычно, остальные могут поучаствовать в нем вне конкурса.

Задачи для вас были подготовлены группой авторов в составе: Павел Холкин (HolkinPV), Иван Фефер (Fefer_Ivan), Игорь Кудряшов (Igor_Kudryashov) и Геральд Агапов (Gerald). Как обычно, хочется поблагодарить Михаила Мирзаянова (MikeMirzayanov) за прекрасную систему Codeforces и Марию Белову (Delinur), которая переводила условия.

Распределение баллов по задачам стандартное.

Всем участникам соревнования мы желаем удачи, успешных взломов и высокого рейтинга!

UPD: контест завершился, надеемся вам понравилось) Поздравляем победителей:

1) AntiFate

2) alicechennan

3) honeyofsistercha

4) Fride

5) bla_bla_bla

UPD2: разбор задач опубликован, его можно найти здесь