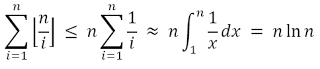When I do ternary search for floating points, I normally do it like this:
while (R - L > EPS) {
double M1 = (2*L + R) / 3;
double M2 = (L + 2*R) / 3;
if (f(M1) <= f(M2)) R = M2;
else L = M1;
}
return f(L);
It works perfectly, but when I try to do it with bitonic arrays (with integer indices), I sometimes get the wrong value, either because I'm off by 1 or because some edge cases don't work.
while (L < R) {
int M1 = (2*L + R) / 3;
int M2 = (L + 2*R) / 3;
if (a[M1] <= a[M2]) R = M2;
else L = M1;
}
return a[L]; // doesn't work :(
I try to address this by looping at the end when the search space is small enough. This addresses the small edge cases and off by 1 errors.
while (L + 3 < R) {
int M1 = (2*L + R) / 3;
int M2 = (L + 2*R) / 3;
if (a[M1] <= a[M2]) R = M2;
else L = M1;
}
int mn = a[L++];
while (L <= R) mn = min(mn, a[L++]);
return mn; // works, but loop is so, yeah
Is there maybe a cleaner way of doing ternary search on arrays without the brute force loop at the end? Like, do I need to tweak the formula for M1 and M2 or something similar?