If you haven't read the camp announcement yet, check it out here: blog
Updates
Since the ICPC prelims will be held again, and due to the short notice, it might be difficult for teams to arrange travel. Therefore, we will be selecting teams based on one of the following criteria:
1. Your past performance in ICPC Regionals/AWC/WF
2. Average rating of your team (~1800+ for Div 2 and ~2100+ for Div 1, with some advantage for 2nd/3rd year students and IOI candidates)
3. Having solved at least 4 problems in the recent prelims round.
Selection Notification:
Selected teams will receive an email confirmation from today onwards (until November 20th).
Div 1 Teams:
Please acknowledge your selection and send your arrival/departure times. This information will help us book your accommodation and arrange travel from New Delhi Airport/Railway Station to the camp location.
Provide the usernames of your teammates who want their names printed on your camp t-shirts.
Submit a cool team motto (similar to what you might write on your regionals photo).
Div 2 Teams:
- In addition to everything mentioned above for Div 1, you will receive a payment link to confirm your slot in the camp.
Div 1 vs. Div 2 Preference:
If you believe you were selected for Div 1 but would prefer Div 2, or vice versa, please contact us directly via DM, reply to the selection email, or comment on this blog post.
Registration:
Register here: goforgold website or fill out this form
Note:
Div 2 has limited slots remaining. We will select teams who meet the criteria on a first-come, first-served basis.
We have already shortlisted around 6-7 Div 1 teams and expect some IOI participants to join as well. To ensure a faster discussion pace and cover more ideas, we will limit Div 1 participants to around 30. This means only 2-3 slots are left.












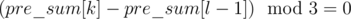
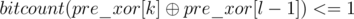
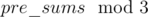 in a
in a 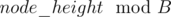 and then taking the index corresponding to the minimum value as
and then taking the index corresponding to the minimum value as 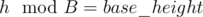 will be marked special. Hence there can be at most
will be marked special. Hence there can be at most 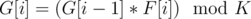
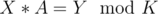 , for some
, for some 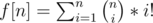 , where
, where 

