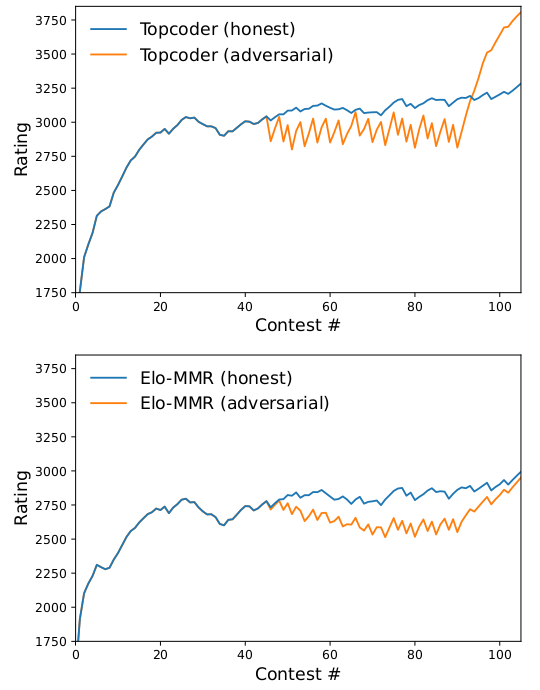
Readers of my Codeforces blog may recall that inutard and I have been experimenting with rating systems for quite some time. Last year, we demonstrated how to break the Topcoder system, and published our findings at the World Wide Web 2021 research conference. There, we derived a new Bayesian rating system from first principles. This system was specifically motivated by sport programming, though it may in theory be applied to any sport that ranks lots of contestants. Recently, it was adopted by the Canadian contest judge, DMOJ.
Now, in collaboration with the CodeChef admins, we are pleased to announce that upon the completion of July Lunchtime, the Elo-MMR rating system goes live on CodeChef.com! While recognizing that any rating system migration will be disruptive, we hope that you’ll find the advantages worthwhile. Let’s briefly go over them. Elo-MMR is:
Principled: using rigorous, peer-reviewed, Bayesian derivations.
Incentive-compatible: it’s never beneficial to score fewer points.
Robust: players will never lose too much rating for a single bad day.
Open: the algorithm and its implementation are available under open licenses.
Fast: on a modern PC, CodeChef’s entire history is processed in under 30 minutes; using close approximations, we’ve further reduced it to under 30 seconds. In addition, Elo-MMR offers:
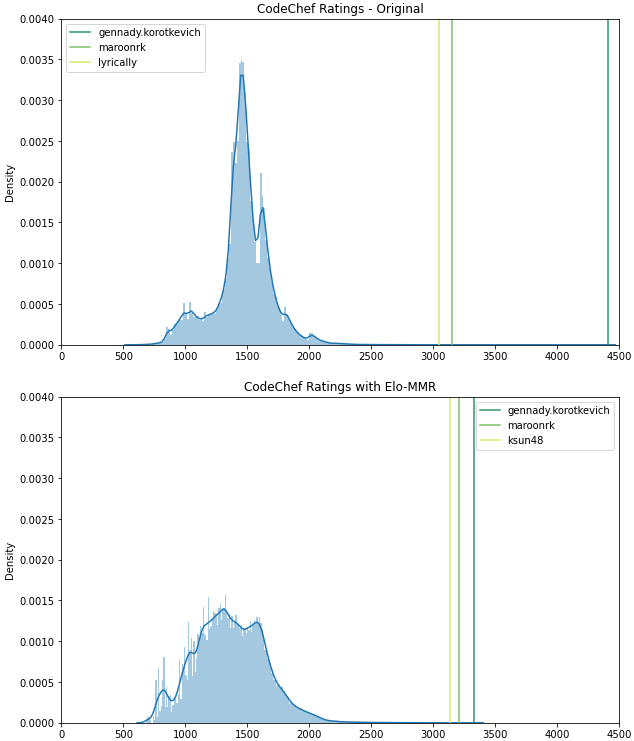
A better rating distribution: CodeChef and Codeforces have a high spread at the top: for instance, tourist / gennady.korotkevich has a 1000+ point lead over CodeChef’s other top users, whereas Elo-MMR brings the gap below 150 points. Conversely, the old systems provide less spread in the low-to-median percentiles, compared to the wider numerical range that Elo-MMR allocates for the majority of users to progress through.
Conservative ratings / newcomer boost: Similarly to Microsoft’s TrueSkill, the publicly displayed rating will be a high-confidence lower bound on the player’s actual skill. As a result, rather than starting at the median and moving down, newcomers will start near the bottom and move up as the system becomes more confident in their skills. This provides a sense of progression and achievement.
Faster convergence for experts: Compared to the previous rating system, Elo-MMR awards a much higher increase to users who do well in their first CodeChef rounds.
It’s worth noting that no special hacks were taken to ensure these properties: they emerge naturally from the mathematical derivation. For details, please see the latest revision of our research article.
To demonstrate the difference in rating distributions, let’s plot them for CodeChef users, using both the old and new (Elo-MMR) rating systems. The latter’s parameters were chosen in such a way as to make the two rating scales approximately comparable. We see that although the original CodeChef ratings take up a wider range overall, gennady.korotkevich alone occupies a big chunk at the upper end! Elo-MMR, on the other hand, spreads the bottom 80% of the population over a wider range.
So, how are we handling the migration to Elo-MMR ratings? One option we considered is to simply take the current ratings and apply Elo-MMR updates from now on. This is not ideal, since rating systems can take a long time to converge: for example, consider the rating distribution of any programming contest site in its first year of operation. At the opposite extreme, we can retroactively recompute all contests in CodeChef’s history using Elo-MMR. DMOJ took this approach; it better leverages the site’s history, but the resulting transition is very sharp.
To smooth it out, CodeChef retroactively computed everyone’s current Elo-MMR ratings in the backend, but will continue to show the original CodeChef rating. Every time you compete, your backend Elo-MMR (MM) rating will be updated, and then your public CodeChef (CC) rating will be pulled closer to your MM rating according to the formula:
where $$$n$$$ is the number of rounds in which you’ve taken part. Thus, new players, who do not yet have a solidified CC rating, are transitioned into the new system more rapidly. The most experienced players are pulled one-fourth of the way each time they compete.
Having examined the population, we might also ask how much the ratings of specific individuals change between the two systems. To find out, we first eliminate the noisiest data: players who have been caught cheating, and newcomers with at most 10 lifetime contest participations. For all remaining users, we compare their original CodeChef rating to their retroactively computed Elo-MMR ratings. The statistics are summarized as follows:
World champion gennady.korotkevich is the main outlier, with $$$CC - MM = 1079$$$. Thus, over the next 10 or so contests that it will take for the new ratings to come into effect, he is expected to lose about $$$1000$$$ points. Thanks Gennady, for understanding and being fine with this!
Less than 800 additional users have $$$CC - MM > 200$$$, and none of these are over $$$500$$$. Nonetheless, these users’ ratings will most likely decrease over their next few contests.
Around 8000 users have $$$MM - CC > 200$$$, the highest of them being $$$630$$$. These players will experience a rating boost over their next few contests.
All other users have $$$|MM - CC| \le 200$$$, so they will experience minimal disruptions.
For the next few months, the day after every rated contest, we will update everyone's hidden Elo-MMR rating in this drive (warning: it might be too large to view online). This way, interested users can investigate their "true" rating trajectories. Within a year, CodeChef will retire the migration plan and simply assign all users their full Elo-MMR rating.
We welcome any questions and will do our best to answer them all!