Contest Link: Replay of Intra PSTU Independence Day Programming Contest — 2024
Announcement : Blog Link
Author : Knightshade
Coming soon...
#include <bits/stdc++.h>
using namespace std;
#define rall(x) x.rbegin(), x.rend()
#define all(x) x.begin(), x.end()
#define sz(x) (int)x.size()
#define ll long long
const ll MOD = 1e9 + 7;
const int MXN = 2e5 + 5;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
int res = 1;
int depth[MXN], pnt[MXN];
vector<vector<int>> graph(MXN);
void dfs(int node, int par)
{
depth[node] = depth[par] + 1;
res = max(depth[node], res);
for (int child : graph[node])
{
if (child == par || pnt[child] <= pnt[node]) continue;
dfs(child, node);
}
}
void sol(int tc)
{
int node, start;
cin >> node >> start;
for (int ii = 1; ii <= node; ++ii)
cin >> pnt[ii];
for (int ii = 1; ii < node; ++ii)
{
int u, v;
cin >> u >> v;
graph[u].push_back(v);
graph[v].push_back(u);
}
dfs(start, start);
cout << res << "\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T = 1;
// cin >> T;
for (int ii = 1; ii <= T; ++ii)
sol(ii);
}
Author : AIpha_Q
Number of ways to re-arrange a string of length $$$n$$$ is $$$(n!) / (a! * b! * c! ...z!)$$$. Here $$$a, b, c, ... z$$$ are the number of occurrences of the letter $$$a, b, c, ...z$$$ in the string.
As there are ranges L, R — we can use 26 prefix sum arrays to calculate the count of all ranges. Now we can use the formula for every range to calculate the result also we have to use inverse modulo for division.
#include<bits/stdc++.h>
#define FAST_IO ios_base::sync_with_stdio(false); cin.tie(NULL)
#define all(x) (x).begin(), (x).end()
using namespace std;
#define int long long
long long binpow(long long a, long long b, long long _mod){
long long res = 1;
while (b>0){
if(b&1)res = (res*a)%_mod;
a = (a*a)%_mod;
b>>=1;
}
return res;
}
signed main() {
FAST_IO;
// start
int n, m;
cin>>n>>m;
vector<int> fact(n+10, 1);
int mod = 1e9+7;
for(int i=1; i<n+10; i++){
fact[i] = fact[i-1] * i % mod;
}
string s;
cin>>s;
int psum[26][n+1];
memset(psum, 0, sizeof psum);
for(int i=0; i<n; i++){
int a = s[i] - 'a';
for(int j=0; j<26; j++){
if(a==j){
psum[j][i+1] = psum[j][i] + 1;
}
else psum[j][i+1] = psum[j][i];
}
}
for(int i=0; i<m; i++){
int L, R;
cin>>L>>R;
int sz = R - L + 1;
vector<int> cnt(26, 0);
for(int j=0; j<26; j++){
cnt[j] = psum[j][R] - psum[j][L-1];
}
int nom = fact[sz];
int dnom = 1;
for(auto ii:cnt){
dnom = dnom * fact[ii] % mod;
}
dnom = binpow(dnom, mod-2, mod);
int res = nom * dnom % mod;
res = (res - 1 + mod) % mod;
cout<<res<<"\n";
}
return 0;
}
Author : Knightshade
This is the easiest problem. We just have to count the number of trailing zeros and print the answer based on conditions. Also we have to handle the case n = 0 manually.
#include <bits/stdc++.h>
using namespace std;
#define rall(x) x.rbegin(), x.rend()
#define all(x) x.begin(), x.end()
#define sz(x) (int)x.size()
#define ll long long
const ll MOD = 1e9 + 7;
const int MXN = 2e5 + 5;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
void sol(int tc)
{
int n;
cin >> n;
if (n == 0)
{
cout << "Counterfeit.\n";
return;
}
int cnt = 0;
while (n > 0 && (n % 10 == 0))
n /= 10, ++cnt;
if (cnt == 0) cout << "Ekok.\n";
else if (cnt == 1) cout << "Dashak.\n";
else if (cnt == 2) cout << "Shatak.\n";
else cout << "Counterfeit.\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T = 1;
cin >> T;
for (int ii = 1; ii <= T; ++ii)
sol(ii);
}
Author : Knightshade
Coming soon...
#include <bits/stdc++.h>
using namespace std;
#define rall(x) x.rbegin(), x.rend()
#define all(x) x.begin(), x.end()
#define sz(x) (int)x.size()
#define ll long long
const ll MOD = 1e9 + 7;
const int MXN = 1e6 + 5;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
ll coprime[MXN];
int phi[MXN];
void process()
{
for (int ii = 1; ii < MXN;++ii) phi[ii] = ii;
for (int ii = 2; ii < MXN; ++ii)
{
if (phi[ii] != ii) continue;
for (int jj = ii; jj < MXN; jj += ii)
phi[jj] -= phi[jj] / ii;
}
coprime[1] = 1;
for (int ii = 2; ii < MXN; ++ii)
{
coprime[ii] = 1LL * ii * phi[ii] / 2;
coprime[ii] += coprime[ii - 1];
}
}
void sol(int tc)
{
int l, r;
cin >> l >> r;
cout << coprime[r] - coprime[l - 1] << "\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
process();
int T = 1;
cin >> T;
for (int ii = 1; ii <= T; ++ii)
sol(ii);
}
Author : Knightshade
Coming soon...
#include <bits/stdc++.h>
using namespace std;
#define rall(x) x.rbegin(), x.rend()
#define all(x) x.begin(), x.end()
#define sz(x) (int)x.size()
#define ll long long
const ll MOD = 1e9 + 7;
const int MXN = 5e4 + 5;
int dx[] = {1, -1, 0, 0};
int dy[] = {0, 0, 1, -1};
int spf[MXN];
ll coprime[MXN];
ll exp_sum[MXN];
void spf_gen()
{
for (int ii = 2; ii < MXN; ii += 2)
{
if (spf[ii] != 0) continue;
spf[ii] = ii;
if (1LL * ii * ii >= MXN) continue;
for (int jj = ii * ii; jj < MXN; jj += ii)
if (spf[jj] == 0) spf[jj] = ii;
if (ii == 2) --ii;
}
}
void co_gen()
{
ll sum = 0;
for (int ii = 1; ii < MXN; ++ii)
{
sum += 1LL * ii * ii;
exp_sum[ii] = coprime[ii] = sum;
}
vector<pair<int, int>> fac;
auto gen = [&](int n)
{
fac.clear();
fac.push_back({1, 0});
while (n != 1)
{
int prime = spf[n];
while (n % prime == 0) n /= prime;
int len = sz(fac);
for (int ii = 0; ii < len; ++ii)
fac.push_back({fac[ii].first * prime, fac[ii].second ^ 1});
}
fac.erase(fac.begin());
};
for (int ii = 2; ii < MXN; ++ii)
{
gen(ii);
ll bad = 0;
for (auto jj : fac)
{
ll cur = 1LL * jj.first * jj.first * exp_sum[ii / jj.first];
if (!jj.second) cur *= -1;
bad += cur;
}
coprime[ii] -= bad;
}
for (int ii = 1; ii < MXN; ++ii)
coprime[ii] += coprime[ii - 1];
}
void sol(int tc)
{
int l, r;
cin >> l >> r;
cout << coprime[r] - coprime[l - 1] << "\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
spf_gen();
co_gen();
int T = 1;
cin >> T;
for (int ii = 1; ii <= T; ++ii)
sol(ii);
}
Author : AIpha_Q
Comming soon...
#include<bits/stdc++.h>
#define FAST_IO ios_base::sync_with_stdio(false); cin.tie(NULL)
#define all(x) (x).begin(), (x).end()
using namespace std;
#define int long long
int a, b, c, n;
int dp[73][73][73][5][15];
int mod = 1e9+7;
int solve(int a, int b, int c, int tp, int x){
if(x>n || a<0 || b<0 || c<0)return 0;
if(a==0 && b==0 && c==0 && x<=n)return 1;
if(dp[a][b][c][tp][x] != -1)return dp[a][b][c][tp][x];
int res = 0;
if(tp==1){
res += solve(a-1, b, c, tp, x+1) + solve(a, b-1, c, 2, 1) + solve(a, b, c-1, 3, 1);
}
else if(tp==2){
res += solve(a-1, b, c, 1, 1) + solve(a, b-1, c, tp, x+1) + solve(a, b, c-1, 3, 1);
}
else if(tp==3){
res += solve(a-1, b, c, 1, 1) + solve(a, b-1, c, 2, 1) + solve(a, b, c-1, tp, x+1);
}
else res += solve(a-1, b, c, 1, 1) + solve(a, b-1, c, 2, 1) + solve(a, b, c-1, 3, 1);
res %= mod;
return dp[a][b][c][tp][x] = res;
}
signed main() {
FAST_IO;
// start
int t;
cin>>t;
read:
while (t--) {
cin>>a>>b>>c>>n;
for(int i=0; i<a+1; i++){
for(int j=0; j<b+1; j++){
for(int k=0; k<c+1; k++){
for(int l=0; l<4; l++){
for(int m=0; m<n+2; m++){
dp[i][j][k][l][m] = -1;
}
}
}
}
}
int res = solve(a, b, c, 0, 0);
cout<<res<<"\n";
}
return 0;
}
Author : AIpha_Q
Precalculate the occurrences of every letter for every subtree, we can use 26 arrays for that. Then for every subtree, we have to check whether the count of every letter is greater or equal to the the count of every letter of the string.
#include<bits/stdc++.h>
#define FAST_IO ios_base::sync_with_stdio(false); cin.tie(NULL)
#define all(x) (x).begin(), (x).end()
using namespace std;
const int N = 2e5+10;
vector<int> gh[N];
char ar[N];
int cnt[N][26];
void dfs(int node, int par=-1){
int cur = ar[node] - 'a';
cnt[node][cur] = 1;
for(auto v:gh[node]){
if(v==par)continue;
dfs(v, node);
for(int i=0; i<26; i++){
cnt[node][i] += cnt[v][i];
}
}
}
int main() {
FAST_IO;
// start
int n;
cin>>n;
for(int i=1; i<=n; i++){
cin>>ar[i];
}
for(int i=0; i<n-1; i++){
int a, b;
cin>>a>>b;
gh[a].push_back(b);
gh[b].push_back(a);
}
dfs(1);
int m;
cin>>m;
string s;
cin>>s;
vector<int> val(26, 0);
for(int i=0; i<m; i++){
int a = s[i] - 'a';
val[a]++;
}
for(int i=1; i<=n; i++){
bool f = 1;
for(int j=0; j<26; j++){
if(cnt[i][j] < val[j]) f = 0;
}
cout<<f<<" ";
}
cout<<"\n";
return 0;
}
Author : AIpha_Q
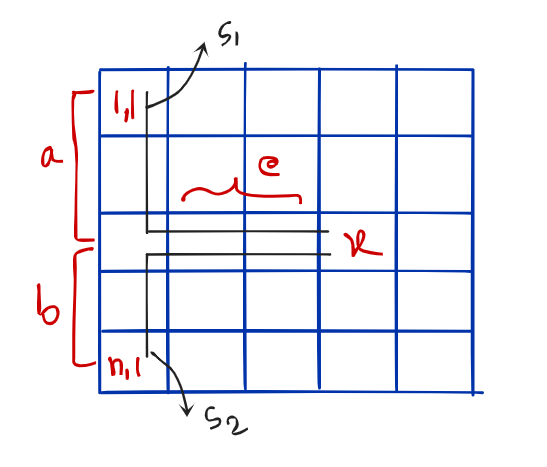
If we think like this image here,
$$$s1 = a + c$$$
$$$s2 = b + c$$$
so, $$$s1 + s2 = a + b + 2c$$$ and $$$a + b = n + 1$$$
from this we can get $$$c = (s1 + s2 - n - 1) / 2$$$
now with the help of c, we can get the position of treasure which is $$$x = s1 - c$$$ and $$$y = c + 2$$$
[see the image above for better understanding]
#include<bits/stdc++.h>
#define FAST_IO ios_base::sync_with_stdio(false); cin.tie(NULL)
using namespace std;
int main() {
FAST_IO;
int t;
cin>>t;
while (t--) {
int n, m;
cin>>n>>m;
int s1, s2;
cin>>s1>>s2;
int c = (s1 + s2 - n - 1)/2;
int x = s1 - c;
int y = c + 2;
cout<<x<<" "<<y<<"\n";
}
return 0;
}










