Hello, codeforces.
I think this technique is important, and easy to code, although I haven't found much about it, so I've decided to make a blog explaining it.This technique allows to compare substrings lexicographically in $$$O (1)$$$ with a preprocessing in $$$O (NlogN)$$$.
As this is my first post on codeforces, please let me know if there are any mistakes.
Prerequisites:
- Basic strings knowledge.
- Sparse Table(Optional).
What Dictionary of Basic Factors is?
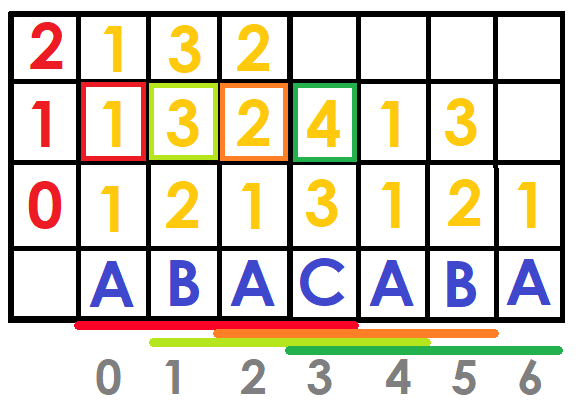
As in the sparse table we will have a matrix of size $$$N\log{N}$$$ called $$$DFB$$$, where $$$DFB[i][j]$$$ tells us the position of the string $$$S[i ... i + 2^j-1]$$$ (the first time it appears) among all the strings of size $$$2^j$$$ ordered lexicographically.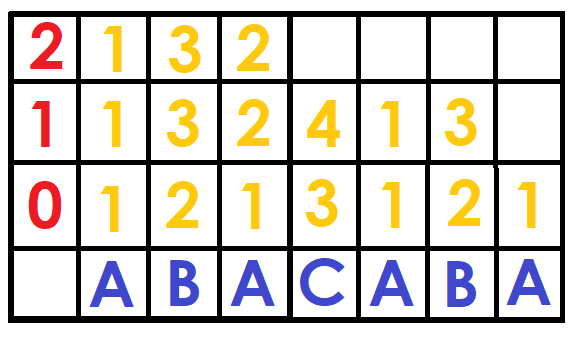
So, how do we build the matrix? Let's start with the lowest level, for powers of size $$$2^0$$$, we simply put the position of the character $$$S[i]$$$ in the dictionary (1 for 'A', 2 for 'B' ... and so on).
For the following $$$ DFB[i][j] $$$ we can save a pair of numbers that are $$$(DFB[i][j-1], DFB[i+2^{j-1}][j-1]) $$$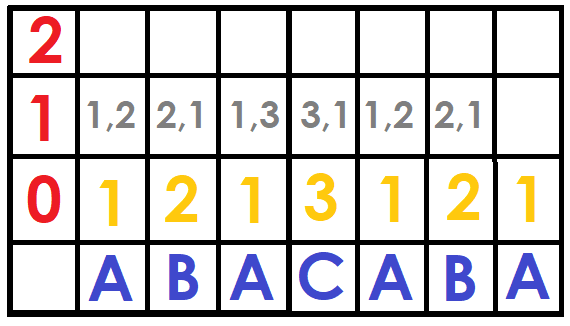
Now we replace the pairs by their position (the first time it appears) in the sorted array of pairs in that power of two, this can be done with Counting Sort in $$$O(N)$$$ (I'll explain it more deeply later), otherwise with a normal sort in $$$O(NlogN)$$$ (But this will slow down the algorithm).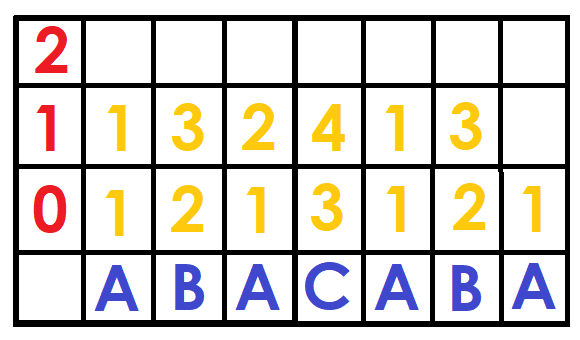
We do that for all powers of two and we will have the complete matrix.
Handling queries:
Suppose we want to make a query that is "Say which of the two substrings $$$S[l_{1}...r_{1}]$$$ and $$$S[l_{2}...r_{2}]$$$ is smaller lexicographically?".
First of all, let's analyze that if the substrings have different sizes, we can compare only the prefixes of size $$$M$$$ where $$$M$$$ is the minimum size between the two substrings, if both prefixes are equal then the smallest lexicographically is the substring of smaller size.
As in the Sparse Table, suppose $$$ k = \ log {(r-l)} $$$, then we can represent the substring $$$ S [l ... r] $$$ as the pair $$$ ( DBF [l] [k], DFB [r-2^k+1] [k] ) $$$. Now to compare two substrings of equal size we simply lexicographically compare their pairs in $$$O(1)$$$.
For example, suppose we have the string "ABACABA" and we want to know which string is lexicographically smaller between $$$ S [0 ... 5] $$$ and $$$ S [1 ... 6] $$$ ("ABACAB" and "BACABA").Since $$$\log{(5-0)}=2$$$, the pairs to compare would be: $$$(DBF [0] [2], DBF [2] [2])$$$ and $$$(DBF [1] [2], DBF [2] [2])$$$, which would be $$$(1,2)$$$ and $$$(2,4)$$$ therefore the first substring is lexicographically smaller.