Hi,
I wanted to explain you the method I used to upsolve the problem of [problem:https://codeforces.me/contest/1478/problem/C].
First of all they define a new kind of thing called symmetric array A[] of where there are n distinct positive integers and n additive inverse (multiplied by -1) of same integers. Whenever a problem define a new property or a thing , I find it better to make some specific and general example of it i.e A = {1, 2, 3, 4, -1, -2, -3, -4} or {a, b, c, d, -a, -b, -c, -d}
Second thing they define are D[] where each i-th term D[i] is the sum of (absolute differences between A[i] to all other possible A[j], j in [1,n]). For ex: n = 3, D[0] = |A[0] - A[0]| + |A[0] - (-A[0])| + |A[0] - A[1]| + |A[0] - (-A[1])| + |A[0] - A[2]| + |A[0] - (-A[2])| Similarly for all other D[1], D[2], D[3], D[4], D[5]. It is easy to see that this D value would be same for A[i] and -A[i].
Question is to tell whether its a valid D[] or not ?
I don't like absolute function but it has this property |negative value| = -1*(negative_value) = positive (basically distances between values or locations) Lets call it distance sum for future reference. so I try to visualize all numbers in sorted order since order of A[] doesn't matter I can freely choose to look at them in sorted way (make a 2d graph) so I get an idea which distance is going to have what value as it always equal to (larger value — smaller value) and its easy to see what is bigger and smaller in a picture.
We are working with a generic example of n = 4 A[] = {a, b, c, d, -a, -b, -c, -d}. I assumed a < b < c < d
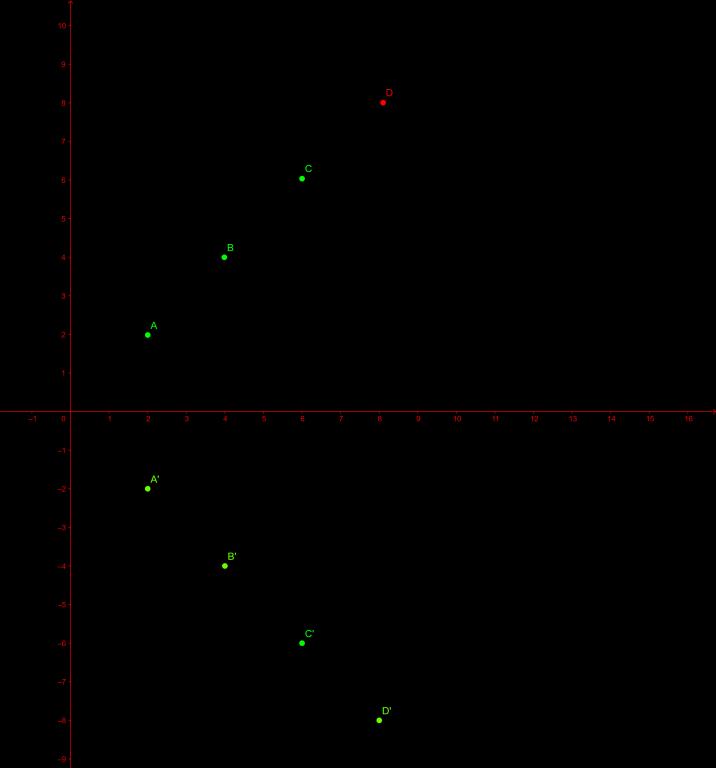
Now lets choose the smallest one and start calculating the total distances from A to every other number. Now from the picture, it might be easy to see why distance sum value would be same for A[i] and -A[i].
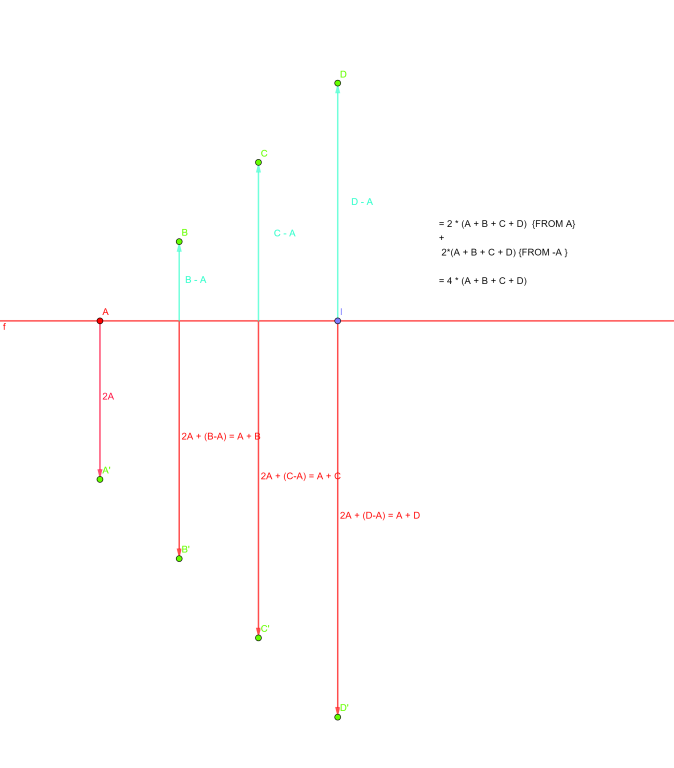
- Here you will see that distance sum for a is 2*(a + b + c + d) and same for -a. I drew the negative terms right below the positive terms for better clarity
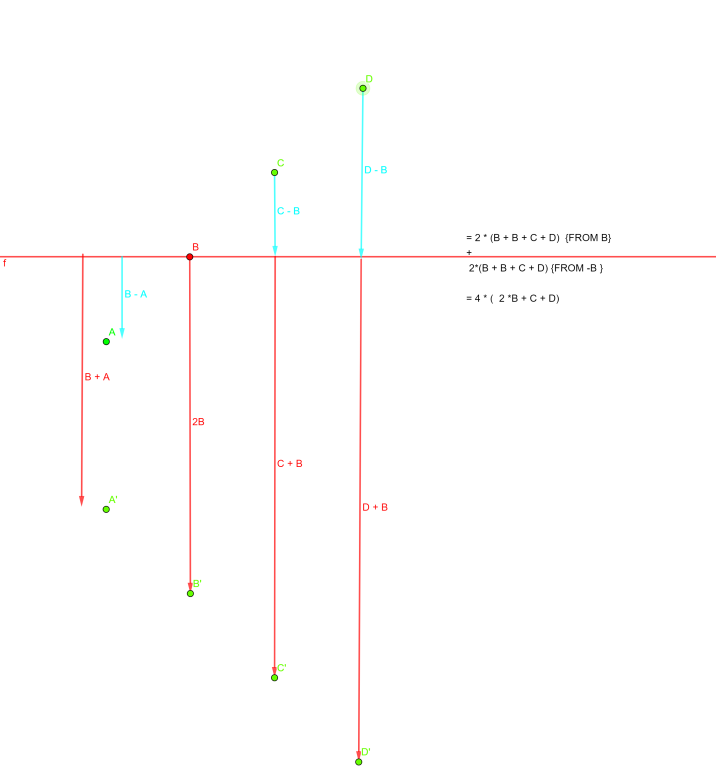

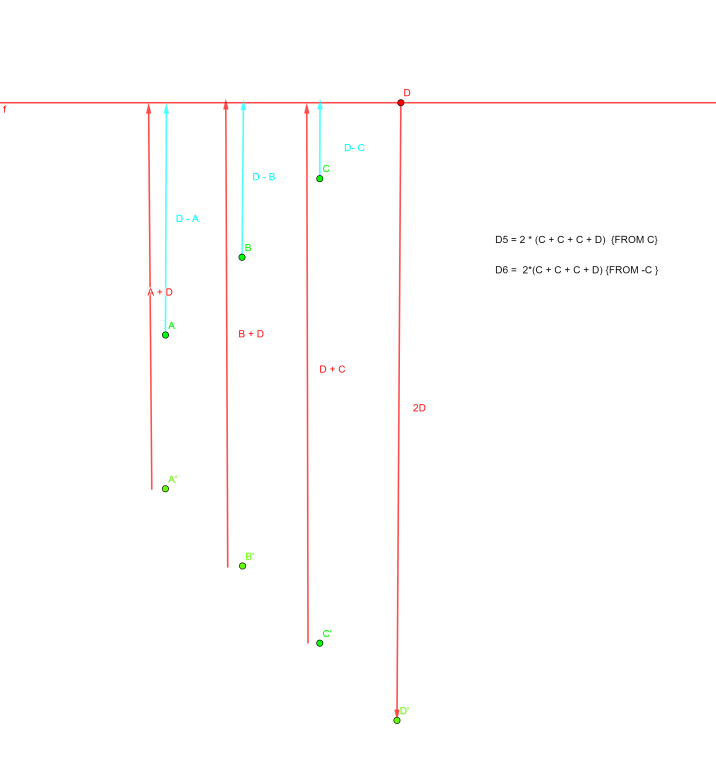
You will notice that distance sum terms are
2 * (a + b + c + d) , 2 * (b + b + c + d), 2 * (c + c + c + d), 2 * (d + d + d + d), 2 * (a + b + c + d) , 2 * (b + b + c + d), 2 * (c + c + c + d), 2 * (d + d + d + d)
They all are even and distinct (if you ignore the distances sum generated by negatives)
looks great to me which means that the largest distance sum is 1. (d * 4) * 2 and in general let's say we sort all distance sum then D[2n] = 2 * n * A[n] => A[n] = D[2n] / (2n) where (D[2n] % (2n))=0 otherwise A[n] will be in floating points which contradicts that A[] are positive distinct integers.
Let's get back to our convenient example of {a, b, c, d, -a, -b, -c, -d} and distance sums as above. 2nd largest distance sum is 2 * (c + c + c + d) and we know d now so we can easily calculate c = (D[6] - 2 * d) / 2 * (3) but generally A[n - 1] = (D[2n - 2] - 2 * A[n] ) / 2 * (n - 1) Note [check if its perfectly dividing and positive after subtracting.] . (We use D[2n-2] because D[2n-1] is same as D[2n] , but you can use std:set and make implementation easy at log(n) insertion cost)
You can get the whole A[] back like this. Lastly check that they is no zero created as it also contradicts the properties of A[]. If you want to check my code 105777562. Yeah this was a long tutorial but I hope its understandable. If anyone has a suggestion on how to improve the reasoning Please share it. Thank you.






