Hello, Codeforces!↵
↵
This blog is heavily inspired by [user:TLE,2020-10-22]'s blog [using merging segment tree to solve problems about sorted list](https://codeforces.me/blog/entry/49446). I don't know exactly how well known this data structure is, but I thought it would be nice to share it anyway, along with some more operations that are possible with it.↵
↵
What it can do↵
------------------↵
↵
We want a data structure that we can think of a set/multiset of **non-negative integers**, or even as a sorted array. We want to support all of the following operations:↵
↵
1. Create an empty structure;↵
2. Insert an element to the structure;↵
3. Remove an element from the structure;↵
4. Print the $k$'th smallest element (if we think of the structure as a sorted array $a$, we are asking for $a[k]$);↵
5. Print how many numbers less than $x$ there are in the set (similar to lower_bound in a std::vector);↵
6. Split the structure into two: one containing the $k$ smallest elements, and the other containing the rest;↵
7. Merge two structures into one (no extra conditions required).↵
↵
Turns out that, if all elements are not greater than $N$, we can perform any sequence of $t$ such operations in $\mathcal{O}(t \log N)$, meaning that each operation costs $\mathcal{O}(\log N)$ amortized (as we will see, all operations except for (7) have worst case $\mathcal{O}(\log N)$).↵
↵
How it works↵
------------------↵
↵
We are going to use a dynamic segment tree to represent the elements. Think of each of them as an index, a leaf on a segment tree. We want the segment tree do be dynamic (we only create the nodes when we need them).↵
↵
So, initially, there are no nodes on the structure (grey nodes are not present in the structure):↵
↵
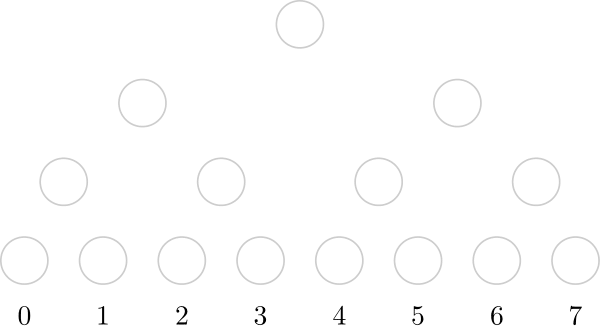↵
↵
If we insert the value $2$, we need to create the path from the root to the leaf that represents $2$. It is also useful to store, on each node, the number of created leafs on that node's subtree.↵
↵
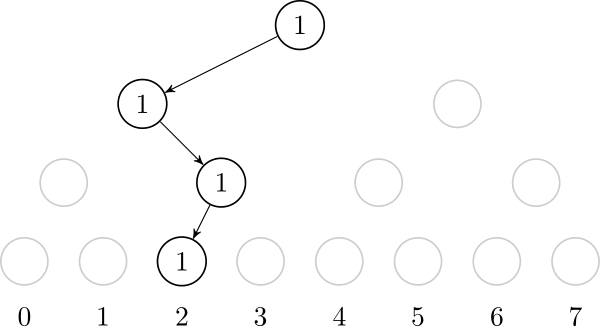↵
↵
Let's also add $1$, $4$ and $5$. In the end, the tree will look like this:↵
↵
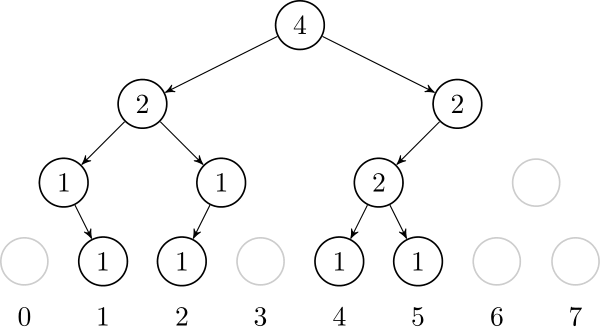↵
↵
Using this representation, it is very straightforward to implement operations (1), (2) and (3). Operations (4) and (5) are also easy, they are classic segtree operations. To do operation (6), we can go down the tree and either call recursively to the left or right child. Here is a pseudocode of this operation:↵
↵
~~~~~↵
node* split(node*& i, int k) {↵
if (!k or !i) return NULL;↵
node* ret = new node();↵
if (i is a leaf) {↵
i->cnt -= k; // assuming multiset↵
ret->cnt += k;↵
} else {↵
if (k <= i->left->cnt) ret->left = split(i->left, k); // split the left↵
else { // take everything from the left and split the right↵
ret->left = i->left;↵
ret->right = split(i->right, k - i->left->cnt);↵
i->left = NULL;↵
}↵
}↵
return ret;↵
}↵
~~~~~↵
↵
It is clear that all these operations cost $\mathcal{O}(\log N)$. On operation (6), note that we only go down recursively to the left or to the right child.↵
↵
But what about operation (7)? It turns out that we can merge two structures in the following way: to merge the subtrees defined by nodes `l` and `r`, if one of them is empty, just return the other. Otherwise, recursively merge `l->left` and `r->left`, and `l->right` and `r->right`. After that, we can delete either `l` or `r`, because they are now redundant: we only need one of them.↵
↵
Now let's see why any sequence of $t$ operations will take $\mathcal{O}(t \log N)$ time. The number of nodes we create is bounded by $\mathcal{O}(t \log N)$, because each operation creates at most $\mathcal{O}(\log N)$ nodes. Now note that the merge algorithm either returns in $\mathcal{O}(1)$, or it deletes one node. So total number of times the algorithm doesn't return in $\mathcal{O}(1)$ is bounded by the total number of created nodes, so it is $\mathcal{O}(t \log N)$.↵
↵
Implementation↵
------------------↵
↵
There are some implementation tricks that make the code easier to write and use. Firstly, we don't need to set $N$ as a constant. Instead, we can have $N = 2^k-1$ for some $k$, and if we want to insert an element larger than $N$, we can just increase $k$, and update the segment tree (we will only need to create a new root, and set its left child to the old root).↵
↵
Also, it's easy to change between set and multiset representation. It is also easy to insert $x$ occurrences of an element at once, just increase the `cnt` variable of the respective leaf accordingly.↵
↵
This implementation uses $\mathcal{O}(t \log N)$ of memory, for $t$ operations.↵
↵
<spoiler summary="Code">↵
~~~~~↵
template<typename T, bool MULTI=false, typename SIZE_T=int> struct sms {↵
struct node {↵
node *l, *r; // left and right childs↵
SIZE_T cnt; // subtree leaf count↵
node() : l(NULL), r(NULL), cnt(0) {}↵
void update() { // update subtree leaf count↵
cnt = 0;↵
if (l) cnt += l->cnt;↵
if (r) cnt += r->cnt;↵
}↵
};↵
↵
node* root;↵
T N;↵
↵
sms() : root(NULL), N(0) {}↵
sms(T v) : sms() { while (v >= N) N = 2*N+1; }↵
sms(const sms& t) : root(NULL), N(t.N) { // copy - O(t log(N))↵
for (SIZE_T i = 0; i < t.size(); i++) {↵
T at = t[i];↵
SIZE_T qt = t.count(at);↵
insert(at, qt);↵
i += qt-1;↵
}↵
}↵
sms(initializer_list<T> v) : sms() { for (T i : v) insert(i); }↵
~sms() {↵
vector<node*> q = {root};↵
while (q.size()) {↵
node* x = q.back(); q.pop_back();↵
if (!x) continue;↵
q.push_back(x->l), q.push_back(x->r);↵
delete x;↵
}↵
}↵
↵
friend void swap(sms& a, sms& b) { // O(1) swap↵
swap(a.root, b.root), swap(a.N, b.N);↵
}↵
SIZE_T size() const { return root ? root->cnt : 0; }↵
SIZE_T count(node* x) const { return x ? x->cnt : 0; }↵
void clear() {↵
sms tmp;↵
swap(*this, tmp);↵
}↵
void expand(T v) { // increase N so value 'v' will fit↵
for (; N < v; N = 2*N+1) if (root) {↵
node* nroot = new node();↵
nroot->l = root;↵
root = nroot;↵
root->update();↵
}↵
}↵
↵
node* insert(node* at, T idx, SIZE_T qt, T l, T r) {↵
if (!at) at = new node();↵
if (l == r) {↵
at->cnt += qt;↵
if (!MULTI) at->cnt = 1;↵
return at;↵
}↵
T m = l + (r-l)/2;↵
if (idx <= m) at->l = insert(at->l, idx, qt, l, m);↵
else at->r = insert(at->r, idx, qt, m+1, r);↵
return at->update(), at;↵
}↵
void insert(T v, SIZE_T qt=1) { // insert 'qt' occurrences of 'v'↵
if (qt <= 0) return erase(v, -qt);↵
assert(v >= 0);↵
expand(v);↵
root = insert(root, v, qt, 0, N);↵
}↵
↵
node* erase(node* at, T idx, SIZE_T qt, T l, T r) {↵
if (!at) return at;↵
if (l == r) at->cnt = at->cnt < qt ? 0 : at->cnt - qt;↵
else {↵
T m = l + (r-l)/2;↵
if (idx <= m) at->l = erase(at->l, idx, qt, l, m);↵
else at->r = erase(at->r, idx, qt, m+1, r);↵
at->update();↵
}↵
if (!at->cnt) delete at, at = NULL; // 'cnt' is always positive↵
return at;↵
}↵
void erase(T v, SIZE_T qt=1) { // erase 'qt' occurrences of 'v'↵
if (v < 0 or v > N or !qt) return;↵
if (qt < 0) insert(v, -qt);↵
root = erase(root, v, qt, 0, N);↵
}↵
void erase_all(T v) { // remove all occurrences of 'v'↵
if (v < 0 or v > N) return;↵
root = erase(root, v, numeric_limits<SIZE_T>::max(), 0, N);↵
}↵
↵
SIZE_T count(node* at, T a, T b, T l, T r) const {↵
if (!at or b < l or r < a) return 0;↵
if (a <= l and r <= b) return at->cnt;↵
T m = l + (r-l)/2;↵
return count(at->l, a, b, l, m) + count(at->r, a, b, m+1, r);↵
}↵
SIZE_T count(T v) const { return count(root, v, v, 0, N); }↵
SIZE_T order_of_key(T v) { return count(root, 0, v-1, 0, N); }↵
SIZE_T lower_bound(T v) { return order_of_key(v); }↵
↵
const T operator [](SIZE_T i) const { // i-th smallest element (0 -> smallest)↵
assert(i >= 0 and i < size());↵
node* at = root;↵
T l = 0, r = N;↵
while (l < r) {↵
T m = l + (r-l)/2;↵
if (count(at->l) > i) at = at->l, r = m;↵
else {↵
i -= count(at->l);↵
at = at->r; l = m+1;↵
}↵
}↵
return l;↵
}↵
↵
node* merge(node* l, node* r) {↵
if (!l or !r) return l ? l : r;↵
if (!l->l and !l->r) { // 'l' is a leaf↵
if (MULTI) l->cnt += r->cnt;↵
delete r;↵
return l;↵
}↵
l->l = merge(l->l, r->l), l->r = merge(l->r, r->r);↵
l->update(), delete r;↵
return l;↵
}↵
void merge(sms& s) { // merge two sets↵
if (N > s.N) swap(*this, s);↵
expand(s.N);↵
root = merge(root, s.root);↵
s.root = NULL;↵
}↵
↵
node* split(node*& x, SIZE_T k) {↵
if (k <= 0 or !x) return NULL;↵
node* ret = new node();↵
if (!x->l and !x->r) x->cnt -= k, ret->cnt += k;↵
else {↵
if (k <= count(x->l)) ret->l = split(x->l, k);↵
else {↵
ret->r = split(x->r, k - count(x->l));↵
swap(x->l, ret->l);↵
}↵
ret->update(), x->update();↵
}↵
if (!x->cnt) delete x, x = NULL; // 'cnt' is always positive↵
return ret;↵
}↵
void split(SIZE_T k, sms& s) { // get the 'k' smallest elements↵
s.clear();↵
s.root = split(root, min(k, size()));↵
s.N = N;↵
}↵
// get all elements smaller than 'k'↵
void split_val(T k, sms& s) { split(order_of_key(k), s); }↵
};↵
~~~~~↵
</spoiler>↵
↵
↵
<spoiler summary="How to use">↵
This code can represent either set of multiset. To create an empty structure:↵
↵
~~~~~↵
sms<int> s; // set↵
sms<int, true> s; // multiset↵
sms<int, true, long long> s; // multiset, if you want to insert more than 1e9 elements↵
~~~~~↵
↵
Most of the operations look similar to std::set:↵
↵
~~~~~↵
sms<int, true> s; // multiset↵
s.insert(3); // insert value '3'↵
s.insert(4, 3); // insert value '4' three times↵
s.erase(4); // erase one occurrence of value '4'↵
s.erase(3, 5); // erase 5 occurrences of value '3'↵
s.erase_all(4); // erase all occurrences of value '4'↵
~~~~~↵
↵
Order statistic operations work as well:↵
↵
~~~~~↵
sms<int, true> s = {4, 7, 3, 4, 1, 6, 3}; // now s = {1, 3, 3, 4, 4, 6, 7}↵
cout << s.order_of_key(4) << endl; // prints "3"↵
cout << s[0] << " " << s[3] << " " << s[5] << endl; // prints "1 4 6"↵
~~~~~↵
↵
Finally, split and merge operations look like this:↵
↵
~~~~~↵
sms<int, true> s = {1, 3, 3, 4, 4, 6, 7};↵
sms<int, true> s2;↵
s.split(4, s2); // get the 4 smallest elements from s↵
// now s = {4, 6, 7} and s2 = {1, 3, 3, 4}↵
↵
sms<int, true> s3 = {2, 4, 6};↵
s3.merge(s2);↵
// now s3 = {1, 2, 3, 3, 4, 4, 6}↵
~~~~~↵
↵
</spoiler>↵
↵
Memory optimization↵
------------------↵
↵
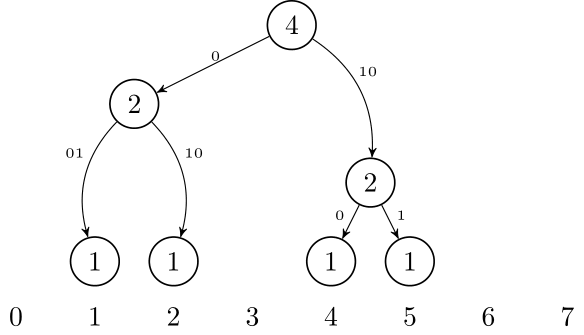
Another way to think about this data structure is as a **trie**. If we want to insert numbers 1, 2, 4, and 5, we can think of them as 001, 010, 100, and 101. After inserting them, it will look like this:↵
↵
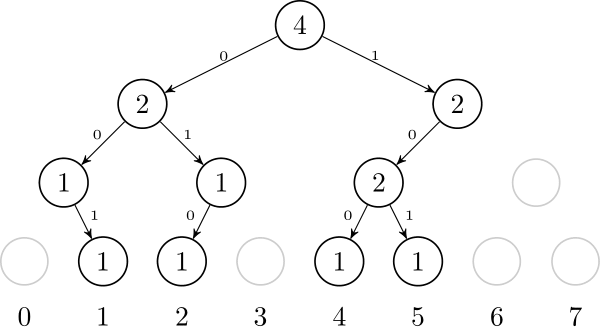↵
↵
Using this idea, it is possible to represent this trie in a compressed form, just like a Patricia Trie or Radix Trie: we only need to store the non-leaf nodes that have 2 children. So, we only need to store nodes that are LCA of some pair of leafs. If we have $t$ leafs, that is $2t-1$ nodes.↵
↵
↵
↵
This is very tricky to implement, but it can reduce the memory usage from $\mathcal{O}(t \log N)$ to $\mathcal{O}(t)$ (see below for implementation).↵
↵
Extra operations↵
------------------↵
↵
There are some more operations you can do with this data structure. Some of them are:↵
↵
1. Insert an arbitrary number of occurrences of the same element;↵
2. You can modify it to use it as a map from int to something, and also have a rule of merging two mappings (for example, if in set $A$ $x$ maps to $u$ and in set $B$ $x$ maps to $v$, it can be made so that in the merged set $x$ maps to $u \cdot v$);↵
3. Using lazy propagation and possibly modifying the merge function, it is possible to do operations like insert a range of values (insert values $a, a+1, a+2, \dots b$ all at once), or flip a range of values (for every $x \in [a, b]$, if it is in the set, remove it, otherwise insert it), etc, maintaining the complexity of all operations;↵
4. I haven't implemented this, but it should bet is possible to use an implicit treap (or other balanced binary search tree) to represent an array, so that in each node of the treap you store a sorted subarray represented by this structure. Using this, we can do all of the usual operations of implicit tree such as split, concatenate, reverse, etc (but not lazy updates); however we can also **sort** a subarray (increasing or decreasing). To sort a subarray, just split the subarray into a treap and merge all of the subarray structures. The time complexity should beis $\mathcal{O}((n+t)(\log n + \log N))$ for $t$ operations on an array of size $n$.↵
↵
Downsides↵
------------------↵
↵
The memory consumption of the data structure might be a problem, though it can be solved with a more complicated code. The code is already not small at all. Another big downside is the amortized complexity, which leaves us with almost no hope to do rollbacks or to have this structure persistent. Also, the constant factor seems to be quite big, so the structure is not so fast.↵
↵
Final remarks↵
------------------↵
↵
The core of the idea was already explained on [user:TLE,2020-10-22]'s blog, and I also found [this paper](https://drops.dagstuhl.de/opus/volltexte/2016/6028/) which describes its use as a dictionary (map). Furthermore, while I was writing this, [user:retrograd,2020-10-22] posted a very cool [blog](https://codeforces.me/blog/entry/83170) where he shows an easier way to have the memory optimization, but it seems to make the split operation more complicated.↵
↵
Problems↵
------------------↵
↵
Using this structure to solve these problems is an overkill, but they are the only examples I got.↵
↵
- [problem:911G]↵
↵
<spoiler summary="Solution">↵
Create $\max(a_i)$ instances of this structure, and store on structure $i$ the indices of occurrences of value $i$ on the array. Processing the operations is trivial using split and merge operations.↵
↵
Code: [submission:88134799]↵
↵
Complexity: $\mathcal{O}((n+q) \log n)$↵
↵
Editorial complexity: $\mathcal{O}(n + q \log (q) \max(a_i))$↵
</spoiler>↵
↵
- [problem:558E]↵
↵
<spoiler summary="Solution">↵
We can represent the array as a concatenation of sorted subarrays, each of them represented by an instances of this structure (inictially each of them will contain a single character). If we want to sort a subarray, just split the corresponding structures (if needed) and then merge all of the structures between $i$ and $j$. We only make $\mathcal{O}(n+q)$ splits in total, so the total number of merges is also bounded by that. To sort decreasingly, just have a flag that indicates that that subarray is actually decreasing, and that flag will be used only when we want to split that subarray at an index, then if that flag is set, we need to mirror that index accordingly. You can also check out [user:TLE,2020-10-22]'s explanation [here](https://codeforces.me/blog/entry/49446?#comment-392898).↵
↵
Code:[submission:91312981]↵
↵
Complexity: $\mathcal{O}((n+q)(\log 26 + \log n))$↵
↵
Editorial complexity: $\mathcal{O}(n + q * 26 * \log n)$↵
↵
</spoiler>↵
↵
**UPD:** I have implemented the memory optimization for segment trees, you can check it out here: [108428555](https://codeforces.me/edu/course/2/lesson/4/1/practice/contest/273169/submission/108428555) (or, alternatively, use this [pastebin](https://pastebin.com/3tMK3d8G)) Please let me know if there is a better way to implement this.
↵
This blog is heavily inspired by [user:TLE,2020-10-22]'s blog [using merging segment tree to solve problems about sorted list](https://codeforces.me/blog/entry/49446). I don't know exactly how well known this data structure is, but I thought it would be nice to share it anyway, along with some more operations that are possible with it.↵
↵
What it can do↵
------------------↵
↵
We want a data structure that we can think of a set/multiset of **non-negative integers**, or even as a sorted array. We want to support all of the following operations:↵
↵
1. Create an empty structure;↵
2. Insert an element to the structure;↵
3. Remove an element from the structure;↵
4. Print the $k$'th smallest element (if we think of the structure as a sorted array $a$, we are asking for $a[k]$);↵
5. Print how many numbers less than $x$ there are in the set (similar to lower_bound in a std::vector);↵
6. Split the structure into two: one containing the $k$ smallest elements, and the other containing the rest;↵
7. Merge two structures into one (no extra conditions required).↵
↵
Turns out that, if all elements are not greater than $N$, we can perform any sequence of $t$ such operations in $\mathcal{O}(t \log N)$, meaning that each operation costs $\mathcal{O}(\log N)$ amortized (as we will see, all operations except for (7) have worst case $\mathcal{O}(\log N)$).↵
↵
How it works↵
------------------↵
↵
We are going to use a dynamic segment tree to represent the elements. Think of each of them as an index, a leaf on a segment tree. We want the segment tree do be dynamic (we only create the nodes when we need them).↵
↵
So, initially, there are no nodes on the structure (grey nodes are not present in the structure):↵
↵
↵
↵
If we insert the value $2$, we need to create the path from the root to the leaf that represents $2$. It is also useful to store, on each node, the number of created leafs on that node's subtree.↵
↵
↵
↵
Let's also add $1$, $4$ and $5$. In the end, the tree will look like this:↵
↵
↵
↵
Using this representation, it is very straightforward to implement operations (1), (2) and (3). Operations (4) and (5) are also easy, they are classic segtree operations. To do operation (6), we can go down the tree and either call recursively to the left or right child. Here is a pseudocode of this operation:↵
↵
~~~~~↵
node* split(node*& i, int k) {↵
if (!k or !i) return NULL;↵
node* ret = new node();↵
if (i is a leaf) {↵
i->cnt -= k; // assuming multiset↵
ret->cnt += k;↵
} else {↵
if (k <= i->left->cnt) ret->left = split(i->left, k); // split the left↵
else { // take everything from the left and split the right↵
ret->left = i->left;↵
ret->right = split(i->right, k - i->left->cnt);↵
i->left = NULL;↵
}↵
}↵
return ret;↵
}↵
~~~~~↵
↵
It is clear that all these operations cost $\mathcal{O}(\log N)$. On operation (6), note that we only go down recursively to the left or to the right child.↵
↵
But what about operation (7)? It turns out that we can merge two structures in the following way: to merge the subtrees defined by nodes `l` and `r`, if one of them is empty, just return the other. Otherwise, recursively merge `l->left` and `r->left`, and `l->right` and `r->right`. After that, we can delete either `l` or `r`, because they are now redundant: we only need one of them.↵
↵
Now let's see why any sequence of $t$ operations will take $\mathcal{O}(t \log N)$ time. The number of nodes we create is bounded by $\mathcal{O}(t \log N)$, because each operation creates at most $\mathcal{O}(\log N)$ nodes. Now note that the merge algorithm either returns in $\mathcal{O}(1)$, or it deletes one node. So total number of times the algorithm doesn't return in $\mathcal{O}(1)$ is bounded by the total number of created nodes, so it is $\mathcal{O}(t \log N)$.↵
↵
Implementation↵
------------------↵
↵
There are some implementation tricks that make the code easier to write and use. Firstly, we don't need to set $N$ as a constant. Instead, we can have $N = 2^k-1$ for some $k$, and if we want to insert an element larger than $N$, we can just increase $k$, and update the segment tree (we will only need to create a new root, and set its left child to the old root).↵
↵
Also, it's easy to change between set and multiset representation. It is also easy to insert $x$ occurrences of an element at once, just increase the `cnt` variable of the respective leaf accordingly.↵
↵
This implementation uses $\mathcal{O}(t \log N)$ of memory, for $t$ operations.↵
↵
<spoiler summary="Code">↵
~~~~~↵
template<typename T, bool MULTI=false, typename SIZE_T=int> struct sms {↵
struct node {↵
node *l, *r; // left and right childs↵
SIZE_T cnt; // subtree leaf count↵
node() : l(NULL), r(NULL), cnt(0) {}↵
void update() { // update subtree leaf count↵
cnt = 0;↵
if (l) cnt += l->cnt;↵
if (r) cnt += r->cnt;↵
}↵
};↵
↵
node* root;↵
T N;↵
↵
sms() : root(NULL), N(0) {}↵
sms(T v) : sms() { while (v >= N) N = 2*N+1; }↵
sms(const sms& t) : root(NULL), N(t.N) { // copy - O(t log(N))↵
for (SIZE_T i = 0; i < t.size(); i++) {↵
T at = t[i];↵
SIZE_T qt = t.count(at);↵
insert(at, qt);↵
i += qt-1;↵
}↵
}↵
sms(initializer_list<T> v) : sms() { for (T i : v) insert(i); }↵
~sms() {↵
vector<node*> q = {root};↵
while (q.size()) {↵
node* x = q.back(); q.pop_back();↵
if (!x) continue;↵
q.push_back(x->l), q.push_back(x->r);↵
delete x;↵
}↵
}↵
↵
friend void swap(sms& a, sms& b) { // O(1) swap↵
swap(a.root, b.root), swap(a.N, b.N);↵
}↵
SIZE_T size() const { return root ? root->cnt : 0; }↵
SIZE_T count(node* x) const { return x ? x->cnt : 0; }↵
void clear() {↵
sms tmp;↵
swap(*this, tmp);↵
}↵
void expand(T v) { // increase N so value 'v' will fit↵
for (; N < v; N = 2*N+1) if (root) {↵
node* nroot = new node();↵
nroot->l = root;↵
root = nroot;↵
root->update();↵
}↵
}↵
↵
node* insert(node* at, T idx, SIZE_T qt, T l, T r) {↵
if (!at) at = new node();↵
if (l == r) {↵
at->cnt += qt;↵
if (!MULTI) at->cnt = 1;↵
return at;↵
}↵
T m = l + (r-l)/2;↵
if (idx <= m) at->l = insert(at->l, idx, qt, l, m);↵
else at->r = insert(at->r, idx, qt, m+1, r);↵
return at->update(), at;↵
}↵
void insert(T v, SIZE_T qt=1) { // insert 'qt' occurrences of 'v'↵
if (qt <= 0) return erase(v, -qt);↵
assert(v >= 0);↵
expand(v);↵
root = insert(root, v, qt, 0, N);↵
}↵
↵
node* erase(node* at, T idx, SIZE_T qt, T l, T r) {↵
if (!at) return at;↵
if (l == r) at->cnt = at->cnt < qt ? 0 : at->cnt - qt;↵
else {↵
T m = l + (r-l)/2;↵
if (idx <= m) at->l = erase(at->l, idx, qt, l, m);↵
else at->r = erase(at->r, idx, qt, m+1, r);↵
at->update();↵
}↵
if (!at->cnt) delete at, at = NULL; // 'cnt' is always positive↵
return at;↵
}↵
void erase(T v, SIZE_T qt=1) { // erase 'qt' occurrences of 'v'↵
if (v < 0 or v > N or !qt) return;↵
if (qt < 0) insert(v, -qt);↵
root = erase(root, v, qt, 0, N);↵
}↵
void erase_all(T v) { // remove all occurrences of 'v'↵
if (v < 0 or v > N) return;↵
root = erase(root, v, numeric_limits<SIZE_T>::max(), 0, N);↵
}↵
↵
SIZE_T count(node* at, T a, T b, T l, T r) const {↵
if (!at or b < l or r < a) return 0;↵
if (a <= l and r <= b) return at->cnt;↵
T m = l + (r-l)/2;↵
return count(at->l, a, b, l, m) + count(at->r, a, b, m+1, r);↵
}↵
SIZE_T count(T v) const { return count(root, v, v, 0, N); }↵
SIZE_T order_of_key(T v) { return count(root, 0, v-1, 0, N); }↵
SIZE_T lower_bound(T v) { return order_of_key(v); }↵
↵
const T operator [](SIZE_T i) const { // i-th smallest element (0 -> smallest)↵
assert(i >= 0 and i < size());↵
node* at = root;↵
T l = 0, r = N;↵
while (l < r) {↵
T m = l + (r-l)/2;↵
if (count(at->l) > i) at = at->l, r = m;↵
else {↵
i -= count(at->l);↵
at = at->r; l = m+1;↵
}↵
}↵
return l;↵
}↵
↵
node* merge(node* l, node* r) {↵
if (!l or !r) return l ? l : r;↵
if (!l->l and !l->r) { // 'l' is a leaf↵
if (MULTI) l->cnt += r->cnt;↵
delete r;↵
return l;↵
}↵
l->l = merge(l->l, r->l), l->r = merge(l->r, r->r);↵
l->update(), delete r;↵
return l;↵
}↵
void merge(sms& s) { // merge two sets↵
if (N > s.N) swap(*this, s);↵
expand(s.N);↵
root = merge(root, s.root);↵
s.root = NULL;↵
}↵
↵
node* split(node*& x, SIZE_T k) {↵
if (k <= 0 or !x) return NULL;↵
node* ret = new node();↵
if (!x->l and !x->r) x->cnt -= k, ret->cnt += k;↵
else {↵
if (k <= count(x->l)) ret->l = split(x->l, k);↵
else {↵
ret->r = split(x->r, k - count(x->l));↵
swap(x->l, ret->l);↵
}↵
ret->update(), x->update();↵
}↵
if (!x->cnt) delete x, x = NULL; // 'cnt' is always positive↵
return ret;↵
}↵
void split(SIZE_T k, sms& s) { // get the 'k' smallest elements↵
s.clear();↵
s.root = split(root, min(k, size()));↵
s.N = N;↵
}↵
// get all elements smaller than 'k'↵
void split_val(T k, sms& s) { split(order_of_key(k), s); }↵
};↵
~~~~~↵
</spoiler>↵
↵
↵
<spoiler summary="How to use">↵
This code can represent either set of multiset. To create an empty structure:↵
↵
~~~~~↵
sms<int> s; // set↵
sms<int, true> s; // multiset↵
sms<int, true, long long> s; // multiset, if you want to insert more than 1e9 elements↵
~~~~~↵
↵
Most of the operations look similar to std::set:↵
↵
~~~~~↵
sms<int, true> s; // multiset↵
s.insert(3); // insert value '3'↵
s.insert(4, 3); // insert value '4' three times↵
s.erase(4); // erase one occurrence of value '4'↵
s.erase(3, 5); // erase 5 occurrences of value '3'↵
s.erase_all(4); // erase all occurrences of value '4'↵
~~~~~↵
↵
Order statistic operations work as well:↵
↵
~~~~~↵
sms<int, true> s = {4, 7, 3, 4, 1, 6, 3}; // now s = {1, 3, 3, 4, 4, 6, 7}↵
cout << s.order_of_key(4) << endl; // prints "3"↵
cout << s[0] << " " << s[3] << " " << s[5] << endl; // prints "1 4 6"↵
~~~~~↵
↵
Finally, split and merge operations look like this:↵
↵
~~~~~↵
sms<int, true> s = {1, 3, 3, 4, 4, 6, 7};↵
sms<int, true> s2;↵
s.split(4, s2); // get the 4 smallest elements from s↵
// now s = {4, 6, 7} and s2 = {1, 3, 3, 4}↵
↵
sms<int, true> s3 = {2, 4, 6};↵
s3.merge(s2);↵
// now s3 = {1, 2, 3, 3, 4, 4, 6}↵
~~~~~↵
↵
</spoiler>↵
↵
Memory optimization↵
------------------↵
↵
Another way to think about this data structure is as a **trie**. If we want to insert numbers 1, 2, 4, and 5, we can think of them as 001, 010, 100, and 101. After inserting them, it will look like this:↵
↵
↵
↵
Using this idea, it is possible to represent this trie in a compressed form, just like a Patricia Trie or Radix Trie: we only need to store the non-leaf nodes that have 2 children. So, we only need to store nodes that are LCA of some pair of leafs. If we have $t$ leafs, that is $2t-1$ nodes.↵
↵
↵
↵
This is very tricky to implement, but it can reduce the memory usage from $\mathcal{O}(t \log N)$ to $\mathcal{O}(t)$ (see below for implementation).↵
↵
Extra operations↵
------------------↵
↵
There are some more operations you can do with this data structure. Some of them are:↵
↵
1. Insert an arbitrary number of occurrences of the same element;↵
2. You can modify it to use it as a map from int to something, and also have a rule of merging two mappings (for example, if in set $A$ $x$ maps to $u$ and in set $B$ $x$ maps to $v$, it can be made so that in the merged set $x$ maps to $u \cdot v$);↵
3. Using lazy propagation and possibly modifying the merge function, it is possible to do operations like insert a range of values (insert values $a, a+1, a+2, \dots b$ all at once), or flip a range of values (for every $x \in [a, b]$, if it is in the set, remove it, otherwise insert it), etc, maintaining the complexity of all operations;↵
4. I
↵
Downsides↵
------------------↵
↵
The memory consumption of the data structure might be a problem, though it can be solved with a more complicated code. The code is already not small at all. Another big downside is the amortized complexity, which leaves us with almost no hope to do rollbacks or to have this structure persistent. Also, the constant factor seems to be quite big, so the structure is not so fast.↵
↵
Final remarks↵
------------------↵
↵
The core of the idea was already explained on [user:TLE,2020-10-22]'s blog, and I also found [this paper](https://drops.dagstuhl.de/opus/volltexte/2016/6028/) which describes its use as a dictionary (map). Furthermore, while I was writing this, [user:retrograd,2020-10-22] posted a very cool [blog](https://codeforces.me/blog/entry/83170) where he shows an easier way to have the memory optimization, but it seems to make the split operation more complicated.↵
↵
Problems↵
------------------↵
↵
Using this structure to solve these problems is an overkill, but they are the only examples I got.↵
↵
- [problem:911G]↵
↵
<spoiler summary="Solution">↵
Create $\max(a_i)$ instances of this structure, and store on structure $i$ the indices of occurrences of value $i$ on the array. Processing the operations is trivial using split and merge operations.↵
↵
Code: [submission:88134799]↵
↵
Complexity: $\mathcal{O}((n+q) \log n)$↵
↵
Editorial complexity: $\mathcal{O}(n + q \log (q) \max(a_i))$↵
</spoiler>↵
↵
- [problem:558E]↵
↵
<spoiler summary="Solution">↵
We can represent the array as a concatenation of sorted subarrays, each of them represented by an instances of this structure (ini
↵
Code:[submission:91312981]↵
↵
Complexity: $\mathcal{O}((n+q)(\log 26 + \log n))$↵
↵
Editorial complexity: $\mathcal{O}(n + q * 26 * \log n)$↵
↵
</spoiler>↵
↵
**UPD:** I have implemented the memory optimization for segment trees, you can check it out here: [108428555](https://codeforces.me/edu/course/2/lesson/4/1/practice/contest/273169/submission/108428555) (or, alternatively, use this [pastebin](https://pastebin.com/3tMK3d8G)) Please let me know if there is a better way to implement this.





