Consider a harder variation of Codeforces Global Round 6 — Decreasing Debts (1266D) where the first way to consolidate is changed to: (_first suggested in this comment_)
Let $$$d(a,b) > 0$$$ and $$$d(b,d) > 0$$$ such that $$$a \neq b$$$ or $$$b \neq d$$$. We can decrease the $$$d(a,b)$$$ and $$$d(b,d)$$$ by $$$z$$$ and increase $$$d(a,d)$$$ by $$$z$$$, where $$$0 < z \leq \min(d(a,b),d(b,d))$$$.
(replace $$$c$$$ with $$$b$$$)
It can be proven that any valid submission to this problem is also a valid submission to the easier problem, however the reversion is not true. It appears that some people wrongly assumes that the problem is this harder variation and try to solve it with a "repeated shrinking" algorithm:
- Loop through the vertices in some order.
- For each vertex, rewrite all the edges adjacent to that vertex such that it's in-degree or out-degree is 0.
If the order is fixed, then it's possible to hack (sansen's hack looks like this, which works with the order 1, 2, ..., n: 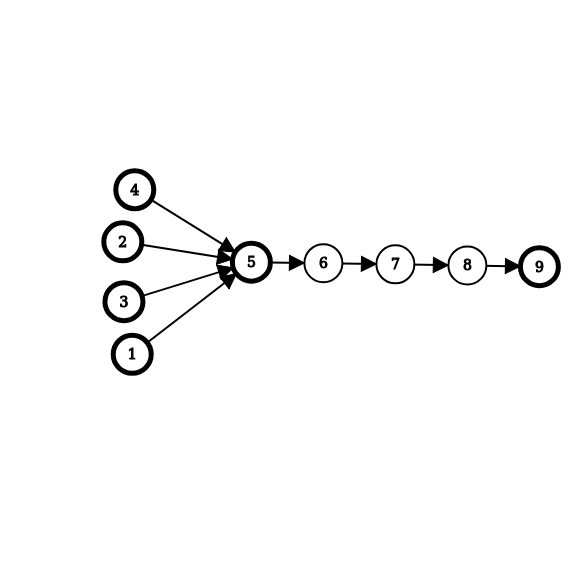 )
)
There are some other possible orders, see hacked submissions for details. (if you submitted some code which uses the shrinking algorithm described here, consider leaving a comment so people can try hacking it)
However, if the order is random shuffled (like in this submission), is it possible to hack the submission? If it isn't possible, then can you prove that the expected number of touched edges is $$$O(n)$$$? (Or $$$O(n log n)$$$)
(There's only one day hour left for uphacking! Please be quick.)






