Hi there!
Consider the following problem: You're given set of n items with weights a1, ..., an. How many ways are there to select k items (order of choosing matters) with total weight of m (let's denote it as bm)? There are two main variants of the problem:
- You may take any item arbitrary number of times. In this case bm = [xm](xa1 + ... + xan)k.
- You may take each item exactly once. In this case bm = m...(1 + yxan)
First case is quite explicit and allows you to calculate answer in like 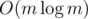 as
as 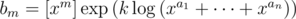 .
.
But what about the second? If you define P(x) = xa1 + ... + xan and Qk(x) = b0 + b1x + b2x2 + ..., you may say for example that Q1(x) = P(x), Q2(x) = P2(x) - P(x2) or Q3(x) = P3(x) - 3P(x)P(x2) + 2P(x3) which allows to calculate Qk(x) for small k quickly. But does anybody know any fast way to calculate Qk(x)? Newton's identities seem to allow something like 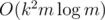 if I'm not mistaken. Can anybody suggest any faster algorithm?
if I'm not mistaken. Can anybody suggest any faster algorithm?






