1106A - Лунный новый год и подсчет крестов
Автор контеста случайно опубликовал разбор задачи в её условии. Необходимо перебрать клетку и проверить, что она является центром креста.
Асимптотика O(n2)
Код:49284766
1106B - Лунный новый год и заказ еды
Заметим, что каждый человек получит либо dj блюд типа tj, либо rtj блюд типа tj и получит целиком и получит некоторый префикс самых дешевых блюд и, возможно, часть запасов какого-либо блюда. Будем поддерживать set доступных блюд, отсортированный по стоимости. На каждой итерации, кроме блюд, которые исчезли навсегда, мы просматриваем не более одного блюда.
Асимптотика 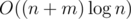
Код:49285005
1106C - Лунный новый год и разделение чисел
Для начала заметим, что в каждой группе должно быть ровно два элемента, так как (a + b)2 > a2 + b2 для положительных a и b
Покажем, что ai и bi должны стоять на "противоположных" позициях в отсортированном массиве, так как
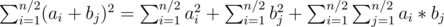
То есть нам надо минимизировать третье слагаемое. Теперь такой выбор ai и bi следует из транснеравенства (доказательтво).
Асимптотика 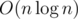
Код:49285168
1106D - Лунный новый год и прогулка
Допустим, мы знаем префикс ответа длины i. Тогда на следующем шаге мы можем пойти в любую вершину, соседнюю с уже посещенной. Очевидно, что стоит идти в вершину с минимальным номером.
Это можно сделать используя bfs с приоритетной очередью.
Асимптотика 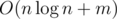
Код:49285447
1106E - Лунный новый год и красные конверты
Задача решается методом динамического программирования. Обозначим за dp[i][j] минимальное количество монет у Боба, если он сейчас выбирает конверт в момент времени i и Алиса уже отвлекла его j раз.
Тогда из dp[i][j] можно перейти в dp[i + 1][j + 1] (если Алиса отвлекает его на i-том ходе) и в dp[dchoice + 1][j], где dchoice — d конверта, который выберет Боб.
Если использовать метод сканирующей прямой, то можно в каждой момент поддерживать set доступных конвертов отсортированный по убыванию w. Тогда мы сможем узнавать выбор Боба на каждой итерации за 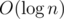 .
.
Асимптотика 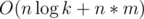
Код:49285694
1106F - Лунный новый год и рекурсивная последовательность
Допустим fk = x и fi = xyi. По малой теореме Ферма 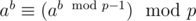 . Значит мы можем считать yi по модулю p - 1. Найдем yn с помощью возведения матрицы в степень.
. Значит мы можем считать yi по модулю p - 1. Найдем yn с помощью возведения матрицы в степень.
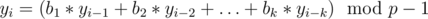
Причем 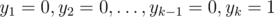
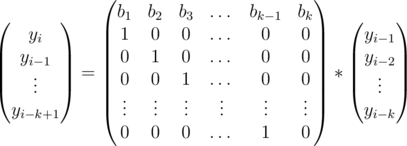
Тогда
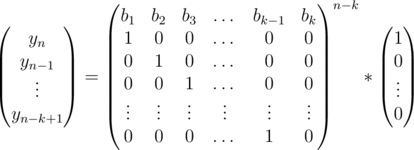
После того, как мы нашли yn используя бинарное возведение матрицы в степень, нам надо решить
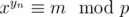
Заметим, что число 3 является первообразным корнем числа 998244353 (степени тройки имеют все возможные остатки по модулю p)
Значит для какого-либо k выполняется 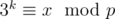
Из этого следует что для такого k верно и 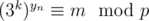 а значит и
а значит и 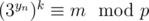
Найдем k, которое подходит под эти свойства.
Обозначим за inv(i) элемент, обратный i по модулю p.
Число k представимо в виде k = f * d + s, где f > s. Возьмем число f примерно равное 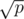
Код:49321335





