Hello, Codeforces!
I think many of Codeforces users know about Mo's algorithm. For those, who don't know, please read this blog.
Canonical version of the algorithm
The canonical implementation of this algorithm gives 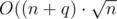 time complexity if insertions and deletions work in O(1).
time complexity if insertions and deletions work in O(1).
Usually, the two comparators for query sorting are used. The slowest one:
struct Query {
int l, r, idx;
inline pair<int, int> toPair() const {
return make_pair(l / block, r);
}
};
inline bool operator<(const Query &a, const Query &b) {
return a.toPair() < b.toPair();
}
We know it can be optimized a little if for even blocks we use the reverse order for the right boundary:
struct Query {
int l, r, idx;
inline pair<int, int> toPair() const {
return make_pair(l / block, ((l / block) & 1) ? -r : +r);
}
};
inline bool operator<(const Query &a, const Query &b) {
return a.toPair() < b.toPair();
}
Achieving a better time complexity
We can achieve 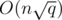 complexity for Mo's algorithm (still assuming that insertions and deletions are O(1). Note that
complexity for Mo's algorithm (still assuming that insertions and deletions are O(1). Note that 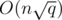 is always better than
is always better than 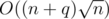 . We can prove it as follows:
. We can prove it as follows:
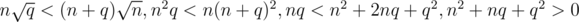
The last statement is always true, so the statement above is proved.
But how this complexity can be achieved?
Relation to TSP
At first, notice that number of operations to change the segment (l1;r1) to (l2;r2) will take |l1 - l2| + |r1 - r2| insertions and deletions.
Denote the queries as (l1;r1), (l2;r2), ..., (lq;rq). We need to permute them to minimize the number of operations, i. e. to find a permutation p1, p2, ... pq such that total number of operations
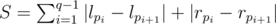
is minimal possible.
Now we can see the relationship between Mo's algorithm and TSP on Manhattan metrics. Boundaries of queries can be represented as points on 2D plane. And we need to find an optimal route to visit all these points (process all the queries).
But TSP is NP-complete, so it cannot help us to find the optimal query sorting order. Instead, we should use a fast heuristic approach. A good approach would be the use of recursive curves. Wikipedia says about using Sierpiński curve as a basis to find a good TSP solution.
But Sierpiński curve is not very convenient in implementation for integer point coordinates, so we will use another recursive curve: Hilbert curve.
Hilbert curve
Let's build a Hilbert curve on a 2n × 2n matrix and pass all the cells on matrix according to this curve. Denote ord(i, j) as the number of cells visited before the cell (i;j) in order of Hilbert curve. The following picture shows ord(i, j) for each cell on 8 × 8 matrix:






