Существует ли полиномиальный (возможно, субоптимальный) алгоритм для нахождения остовного дерева с минимальным числом поворотов, на графе, представляющем из себя связное подмножество клеток грида (возможно, невыпуклое и с дырками).

Поворотом называется пара ребер, имеющих общий конец и направленных перпендикулярно по отношению друг к другу.

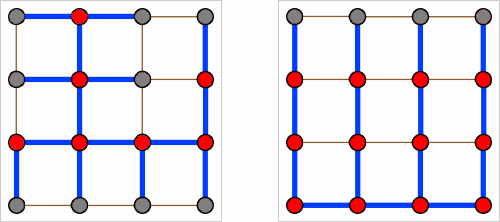
Например, на картинке ниже с гридом 4 x 4 (в данном случае прямоугольном, но может иметь любую форму, если рассматривать только подмножество клеток грида) остовное дерева справа (6 поворотов) лучше, чем остовное дерево слева (14 поворотов)