Hello Everyone, Chef And Interval Painting was one of the most interesting problem of March Long. I am writing this blog for 2 main reasons listed below.
I am having a hard time in understanding the editorial. And the interesting thing is I haven't even reached to the harder part of the editorial yet i.e. the NTT part. I can't understand the DP relation that they have written in the first statement. How can we say that the number of ways for exactly r colors to be visible at the end won't depend on the choice of colors which are visible? According to me because we are coloring in a specific order which can't be changed, I think it should depend on the choice of colors. It would be great if someone can provide a better approach to arrive at the solution or if someone has a different DP relation that can be used to solve the problem.
The second reason is during the contest I was able to figure out a DP relation which can be used to solve the problem in O(N^2) time. But obviously, I was not able to convert that approach to a better complexity. So, I wanted to share my approach and if anyone can provide a suggestion on is it possible to apply NTT to my approach or not.
So basically, the approach which I used was dp[N][K] will denote the number of distinct coloring of an array of size N after K rounds and the only twist is coloring a subarray of size 0 is also a valid round.
So, the relation would be fairly simple
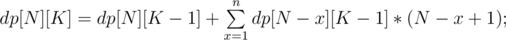
The basic logic used is same that start from reverse and coloring a subarray of any size in some round X won't affect the coloring in the previous i.e. (X-1)th round. And the final answer for some value of N,K will be
I don't know if the above relation can be solved in less time complexity or not. But any suggestion related to the problem are welcomed.
Thanks !!





