(Sorry for my bad english!!)

Problem (QBSEGPAR — Vietnam Olympiad of Informatics 2005): For an integer array a₁, a₂, ..., a_n and a integer k. Determine the smallest integer M to divide the array into k non-empty paths so that the sum of the elements in each paths does not exceed M.

• Constraints: k ≤ n ≤ 15000, |a_i| ≤ 30000.

I have an 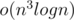solution, which we do binary seaching for M, and dp to check if this M could satisfy (let f(i, j) = true means you could divide array a[1..i] into j paths so that the sum of the elements in each of j paths does not exceed M. Otherwise, f(i, j) = false. Then we can divide array a[1..n] into k satisfied path if f(n, k) = true). Of course this couldn't pass all tests.

Then I checked for the solution. Here is it, we also do binary searching for M, but for each M, we do a different dp:

• f_i = minimum number of paths which has sum of elements does not exceed M that you could divide from array a[1..i].
• g_i = maximum number of paths which has sum of elements does not exceed M that you could divide from array a[1..i].

Required complexity is o(nlogn²). We can calculate f and g by o(nlogn) dp, which need segment tree or Fenwick tree (i haven't done it), or simple o(n²) dp. Okay, now here is the checking path, which is unclear to me: The solution said that array a[1..n] could divide into k satisfied paths if f_n ≤ k ≤ g_n. I think this might not be right. In my opinion, we can divide array a[1..n] into minimum f_n satisfied paths, maximum g_n satisfied paths, but it doesn't mean we can divide the array into k satisfied paths which f_n ≤ k ≤ g_n.

Could you tell me how to prove this solution right or wrong? Thanks for your help!