[problem:A]

One can see that in the final set all the elements less than x should exist, x shouldn't exist and any element greater than x doesn't matter so we will count the number of elements less than x that don't exist in the initial set and add this to the answer, If x exists we'll add 1 to the answer because x should be removed .

Problem author : mahmoudbadawy .

Time complexity : O(n + x) .

Solution link (me) : TODO .

Solution link (mahmoudbadawy) : TODO .

[problem:B]

The tree itself is bipartite so we can run a dfs to partition the tree to the 2 sets, We can't add an edge between any 2 nodes in the same set and we can add an edge between any 2 nodes in different sets so let the number of nodes in the left set be l and the number of nodes in the right set be r, The maximum number of edges that can exist is l * r, n - 1 edges already exist so the maximum number of edges to be added is l * r - n + 1.

Problem author : me .

Time complexity : O(n) .

Solution link (me) : TODO .

Solution link (mahmoudbadawy) : TODO .

[problem:C]

n = 2, x = 0 is the only case with answer "NO" .

Let (PW = 2¹⁷) .

First print 1, 2, ..., n - 3 (The first n - 3 positive integers), Let their bitwise-xor sum be y, If x = y You can add PW,PW * 2 and 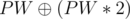, Otherwise you can add 0,PW and .

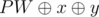Handle n = 1 (print x) and n = 2 (print 0 and x) .

Problem author : mahmoudbadawy .

Solution link (mahmoudbadawy) : TODO .

[problem:D]

In the editorial we suppose that the answer of some query is the number of correct guessed positions which is equal to n-(the hamming distance), The solutions in this editorial consider the answer of a query as n-(real answer), For convenience.

Common things : Let zero(l, r) be a function that returns the number of zeros in the interval [l;r] minus the number of ones in it, We can find it in one query after a preprocessing query, The preprocessing query is 1111..., Let its answer be stores in all_ones, If we made a query with a string full of ones except for the interval [l;r] which will be full of zeros, If this query's answer is cur, zero(l, r) = cur - all, That's because all is the number of ones in the interval plus some trash and cur is the number of zeros in the interval plus the same trash .

First solution by mahmoudbadawy

Let's have a searching interval, initially this interval is [1;n] (The whole string), Let's repeat this until we reach our goal, Let mid = (l + r) / 2 Let's query to get zero(l, mid), If it's equal to r - l + 1, This interval is full of zeros so we can print any index in it as the index with value 0 and continue searching for an index with the value 1 in the interval [mid + 1;r], But if its value is equal to l - r - 1, This interval is full of ones so we can print any index in it as the index with value 1 and continue searching for a 0 in the interval [mid + 1;r], Otherwise we can continue searching for both in the interval [l;mid], Every time the searching interval length must be divided by 2 in any case so we perform O(log(n)) queries .

Second solution by me

Let's send 1111... and let the answer be ans1, Let's send 0111... and let the answer be ans0, We now know the value in the first index (1 if ans1 > ans0, 0 otherwise), We can binary search for the first index where the not-found value exists, which is to binary search on the first value x where zero(2, x) * sign(non - foundbitvalue) ≠ x where sign(y) is 1 if y = 0,  - 1 otherwise .

Problem author : mahmoudbadawy .

Solution link (me) : TODO .

Solution link (mahmoudbadawy) : TODO .

Your thoughts are welcome in the comments .

[problem:E]

Let's write f(j) in another way:-

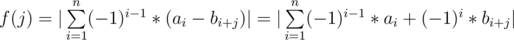
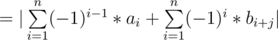
Now we have 2 sums, The first one is constant (doesn't depend on j), For the second sum we can calculate all its possible values using sliding window technique, Now we want a data-structure that takes the value of the first some and chooses the second sum in a good time .

observation: We don't have to try all the possible values of f(j) to minimize the expression if the first sum is c, We can try only the least one greater than  - c and the greatest one less than  - c because for any other f(j) you can prove that the expression will be greater than at least one of them, To do this we can keep all the values of f(j) and try elements numbered lower_bound(-c) and lower_bound(-c)-1 and choose the better.

Now we have a data-structure that can get us the minimum value of the expression once given the value of the first sum in O(log(n)), Now we want to keep track of the value of the first sum .

Let the initial value be c, In each update, If the length of the updated interval is even, The sum won't change because x will be added as many times as it's subtracted, Otherwise x will be added to c or subtracted from c depending of the parity of l (the left-bound of the interval) .

Time complexity : O(n + m + qlog(m)) .

Problem author : mahmoudbadawy .

Solution link (me) : TODO .

Solution link (mahmoudbadawy) : TODO .

[problem:F]

First, Let's get rid of the LCP part .

observation 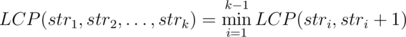, That could make us transform the LCP part into a minimization part by making an array lcp where lcp_i = LCP(s_i, s_i + 1), You could calculate it naively, And when an update happens at index a, You should update lcp_a (If exists) and lcp_a - 1 (If exists) naively .

Now the problem reduces to finding a ≤ l ≤ r ≤ b that maximizes the value

(min_i = l^r - 1lcp_i) * (r - l + 1), If we have a histogram where the i^th column has height lcp_i, The the size of the largest rectangle that fits in the columns from l to r - 1 is the same as our formula so to get rid of finding the l and r part, We can make that histogram and the answer for a query will be the largest rectangle in the histogram the contains the columns from a to b - 1 .

Let BU be a value the we'll choose later, We have 2 cases for our largest rectangle's height h, It could be either h ≤ BU or h > BU, We will solve both problems separately.

For h ≤ BU we can maintain BU segment trees, Segment tree number i has 1 at index x if lcp_x ≤ i and 0 otherwise, When we query it should get us the longest subsegment of ones in the query range, Let's see what we need for our merging operation, If we want the answer for the longest subsegment of ones in a range [l;r], Let mid = (l + r) / 2, Then the answer is the maximum between the answer of [l;mid], The answer of [mid + 1;r], And the maximum suffix of ones in the range [l;mid] added to the maximum prefix of ones in the range [mid + 1;r] . So we need to keep all these information in our node and also the length of the interval, As it's a well-known problem I won't get into more detail. Back to our problem, We can loop over all i ≤ BU, Let the answer for the query on range [a;b - 1] in segment tree number h be w, The maximum width of a rectangle of height i in this range is w, Notice that a width of w in the histogram covers w + 1 strings not w so we'll maximize the answer with h * (w + 1) .

For h > BU, There are 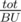(Where tot is the total length of strings in input) columns satisfying this, Let's keep them in a set, When an update happens, You should add the column to the set or remove it depending on its new height, The set's size can't exceed 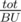now, Let's see how to answer a query, Let's loop over the columns in range [a;b - 1] only, If 2 of them aren't consecutive then the column after the first must have height less than or equal to BU, And the column before the second too, That's because if it weren't, It would be in our set, So we can use this observation by making a new histogram with the columns that satisfy h > BU in the range, And put a column with height 0 between any non-consecutive two, And get the largest rectangle in this histogram by the stack way for example in .

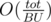Also the answer for our main formula can be an interval of length one, All what I mentioned doesn't cover this, You should maintain another segment tree that gets the maximum value of a range for this .

Maximize all what we got, You have the answer, Now it's time to choose BU, It's optimal in time to choose 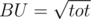but that's not possible because of the memory limit so you have to choose a smaller value .

Optimization: The longest subsegment of ones problem is solved by BU segment trees and each one has 4 integers in each node, You can make them 2 integers (max prefix and suffix of ones) and make another only one segment tree that has the rest of the integers, The would divide the memory by 2 letting you choose bigger BU .

Time complexity : O(tot + q(BU * log(tot) + n / BU))

Problem author : mahmoudbadawy and thanks to vintage_Vlad_Makeev for making it harder and more interesting .

Solution link (vintage_Vlad_Makeev) : TODO .

Solution link (mahmoudbadawy) : TODO .