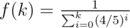Two years ago, the Codeforces rating system was changed significantly. The system is published here.

Let's take a close look at the formula:

• We compute seed_i from old rating, so it corresponds to the performances of all old contests.
• m_i is the mean of seed_i and actual place. Roughly speaking, 50% of it comes from old contests and 50% comes from the most recent contest.
• R corresponds to m_i. 50% of it comes from old contests and 50% comes from the most recent contest.
• The new rating is r_i + d_i = (r_i + R) / 2. 25% comes from the most recent contest and 75% comes from others.

I prefer smaller rating changes in a single contest, at least for negative direction. Some reasons are:

• Why do you put 25% weight on the most recent contest, even for experienced contestants (say, 100+ contests)? However, I agree that if the weight is smaller, it is too time-consuming to raise the rating for newcomers, which can be frustrating. In Glicko (an improved version of Elo), you are assigned a value called RD. This value represents how inaccurate your rating is, and when RD is small, your rating change is smaller. You start from a very high RD, and if you keep competing, this value gradually decreases.

• It is possible that someone suddenly becomes stronger in a short period of time. However, the opposite is not true. Yes, if you don't practice, you may gradually decline, but this is much slower. When someone gets very bad performance, it is natural to think that it was because of a bad luck, not because of actual strength.

• It is simply demotivating to lose way too much rating because of a single failure.

• It seems there was "rating cap" in the old system. For example look at this. His rating changes in #270 and #318 were roughly the same.

What do you think?

UPD. Suggestion for the new formula.

I think slight modification is enough. In the current system, we use

d_i = (R - r_i) / 2

Change it to

d_i = f(k)·(R - r_i)

where k is the number of contests you've participated (so, k = 0 for newcomers).

I suggest f(∞) = 1 / 5, and to compensate that f(0) should be a bit bigger. One possible explicit formula is: