I recently implemented Treap, one of various kinds of binary search trees (BSTs), on Rust. It is a balanced BST, which means that it ensures that tree depth is always 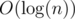where n =  (the number of items in a tree). That is achieved by using randomisation. (For more details see Treap — Wikipedia.)

Experiments

Here are results of some experiments:

(1) Insertion of 10000 elements in the ascending order:
http://ideone.com/tSrw7u
It took 11.7 seconds to insert 30000 elements in the ascending order, and it got Time Limit Exceeded (>15.0sec) when the number of elements is >100000. You'll see that the depth of the treap increases in logarithmic speed.

(2) Insertion of 10000 elements in a random order:
http://ideone.com/yxVe6d
It took 11.8 seconds to insert 30000 elements in a random order. Like (1), the depth of the treap increases in logarithmic speed, too.

Here is a graph that indicates how the depth of the treap grows as the number of elements increases.

/predownloaded/26/3a/263af7e258cf37bd48902f027e4e1f38b016b7d0.png

Conclusion

Treap is an 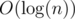-depth balanced tree! Unfortunately, a solution that uses this treap 25637342, which should work in 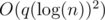-time, got Time limit exceeded. That's probably because of its heavy constant factor.

References

The code I used in these experiments is avaliable at: https://github.com/koba-e964/contest/blob/906fcb07057b72496407b3c6e6a422e48e60dc6f/comm/Treap.rs

My implementation largely depends on the slide ( https://www.slideshare.net/iwiwi/2-12188757 , written in Japanese) by iwiwi.